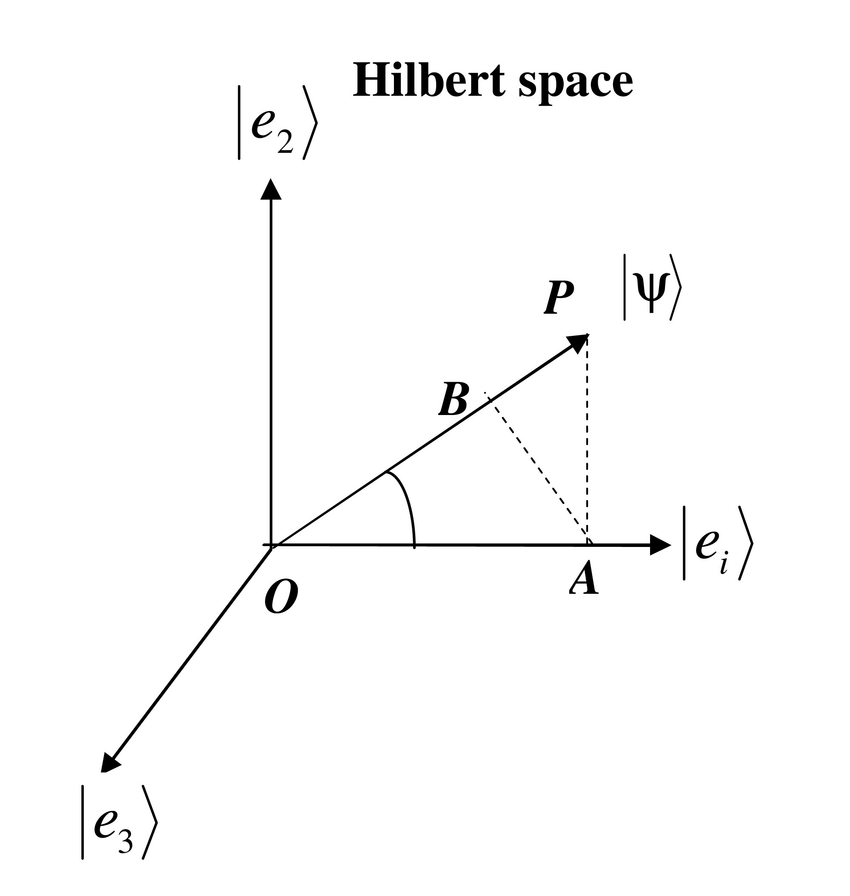
62 فضای هیلبرت
در سلسله فصل هایی به مفاهیم و مطالب مکانیک کوانتوم می پردازم. برای اینکه دستیابی به مطالب ساده تر باشد؛ فصل ها کوتاه ترند تا

در سلسله فصل هایی به مفاهیم و مطالب مکانیک کوانتوم می پردازم. برای اینکه دستیابی به مطالب ساده تر باشد؛ فصل ها کوتاه ترند تا
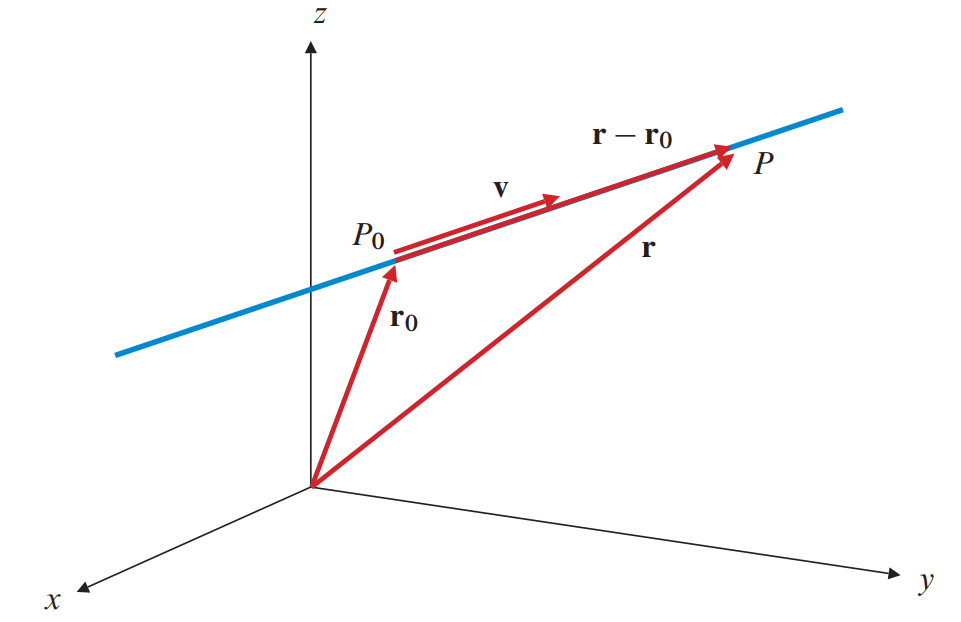
از کنار هم قرار گرفتن نقاط در فضای $\mathbb{R}^3$ ، خط تشکیل می شود. همانطور که در فصل قبل دیدیم؛ محل برخورد دو صفحه غیرموازی
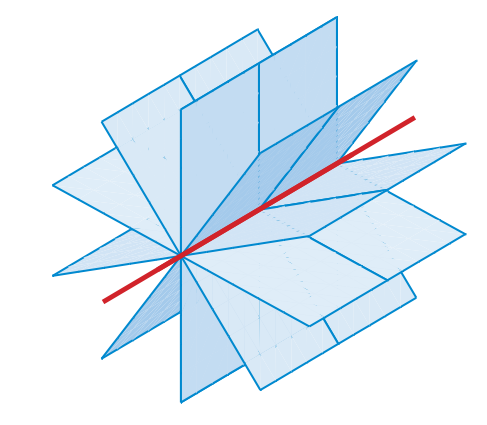
صفحه شکلی دوبعدی است که می خواهیم آن را در فضای سه بعدی بررسی کنیم و معادله صفحه را بدست آوریم. نقطه $P=(x,y,z)$ را در
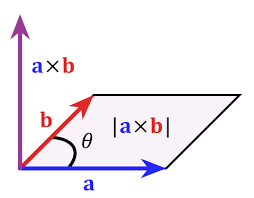
در فصل قبل با ضرب داخلی آشنا شدیم. ضرب خارجی عملی است که دو بردار سه مولفه ای را به عنوان ورودی می گیرد و یک
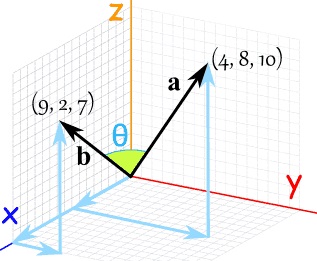
ضرب داخلی (ضرب نقطه ای یا ضرب اسکالر نیز گفته می شود)، عملی است که دو بردار را به عنوان ورودی می گیرد و یک
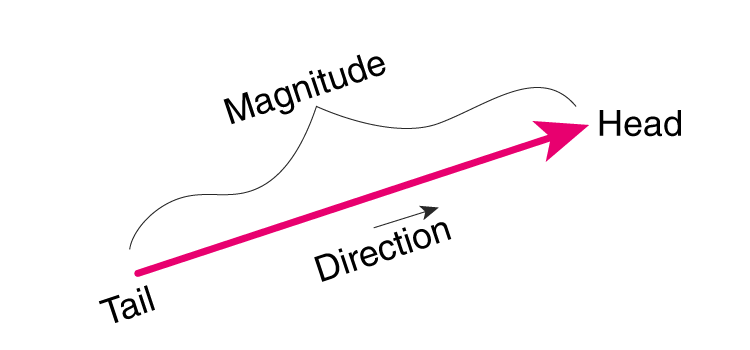
در علوم تجربی، گاها با کمیت هایی روبهرو می شویم که تنها دارای مقدار هستند. به این کمیت ها، کمیت اسکالر یا نرده ای می

ماتریس وارون (Inverse Matrix) مبحث این فصل است. همانند اعداد که در آن، معکوس (وارون) هرعدد ضربدر خود عدد، مساوی یک می شود $a\times a^{-1}=1$
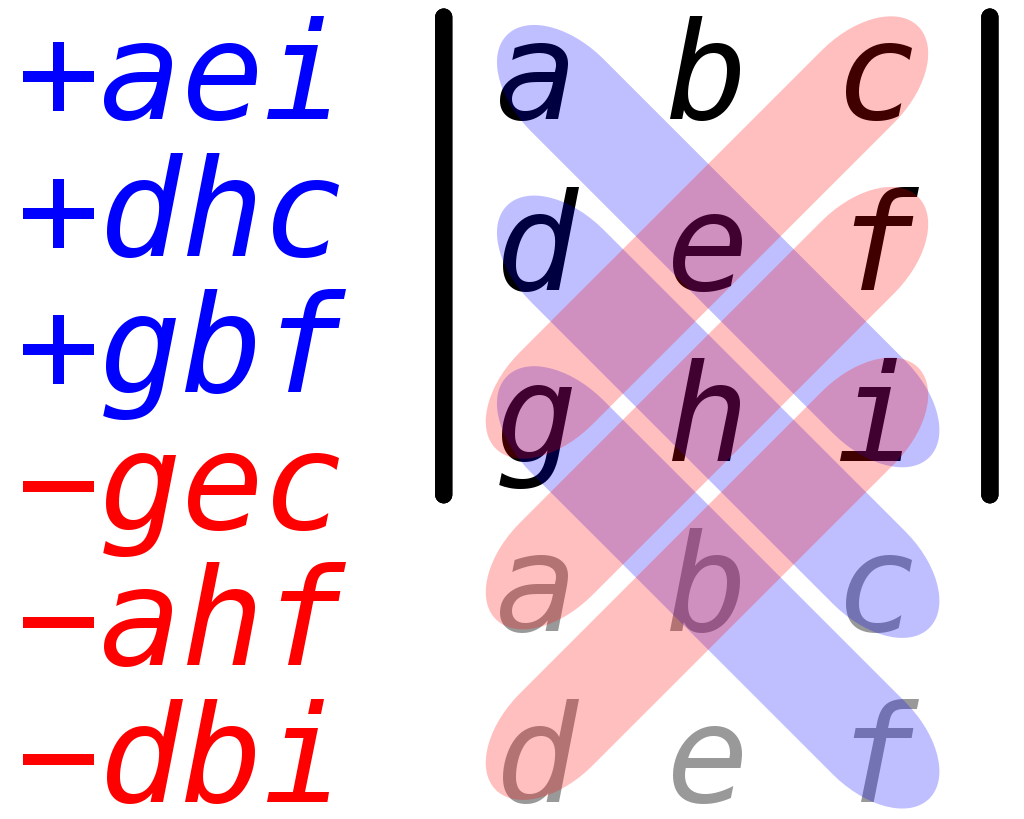
دترمینان (determinant) مفهومی کاربردی در محاسبات ماتریسی است. پس از آشنایی با ماتریس و عملیات های آن، خوب است که با دترمینان آشنا شویم. همانند
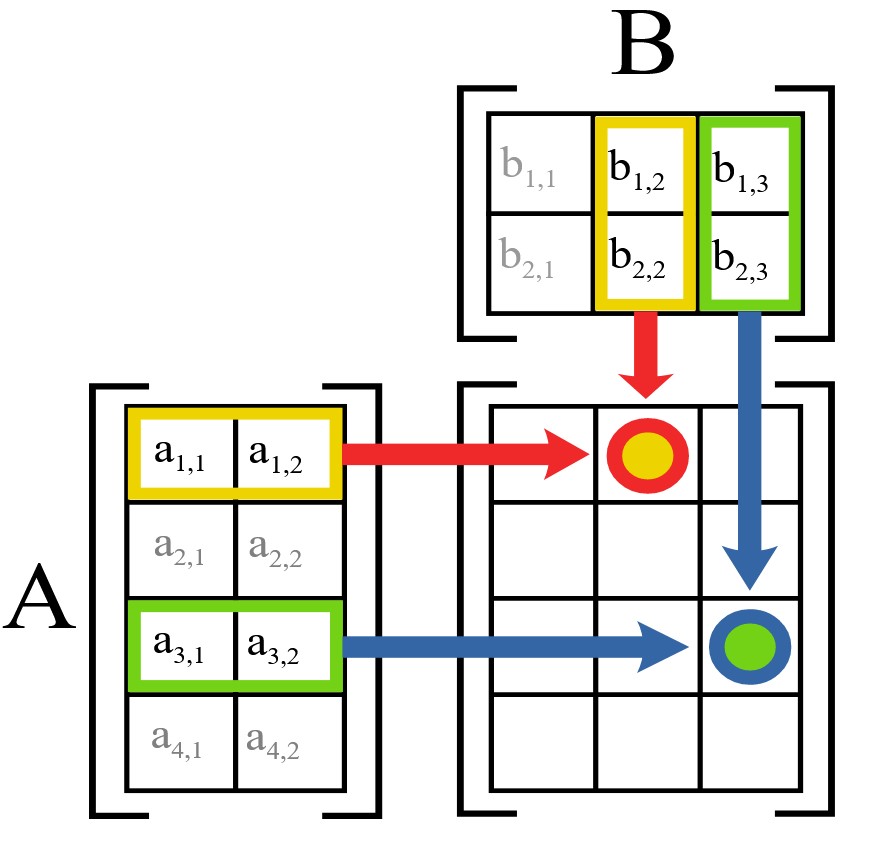
ضرب ماتریسی موضوع این فصل است. پس از آشنایی با مقدمات ماتریس، فراگیری الگوریتم ضرب دو ماتریس حائز اهمیت است. روش ضرب ماتریس ها سرراست

یکی از موضوعات جالب و کاربردی ریاضی، ماتریس (Matrix) است که در جایجای فیزیک، ریاضیات و علوم کامپیوتر ظاهر می شود. بخصوص که ماتریس نقش
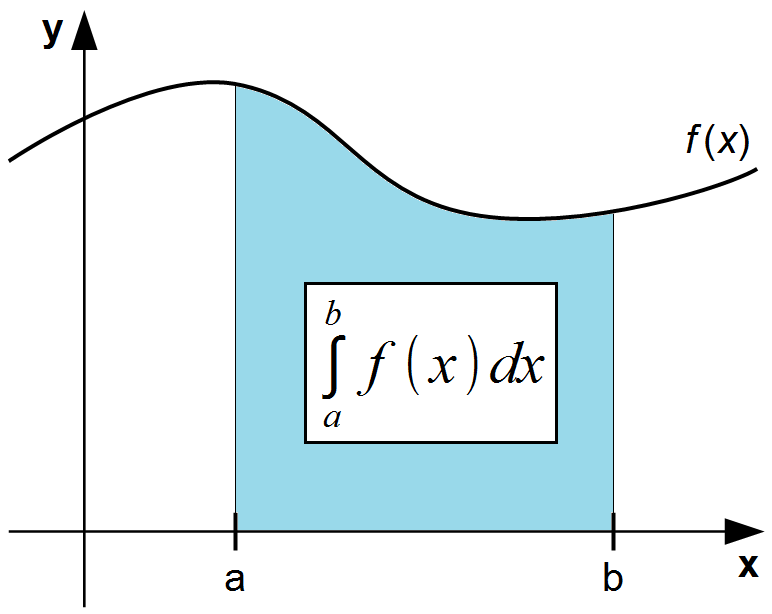
یکی از روش های کارآمد برای حل طیف گسترده ای از انتگرال های پیچیده، روش تغییر متغیر و تبدیل انتگرال به انتگرال های ساده ای

انتگرال گیری جزء به جزء، روشی است که بوسیله آن می توان برخی از انتگرال های حاصل ضرب توابع (که ظاهر دشواری دارند) به سادگی