ضرب داخلی (ضرب نقطه ای یا ضرب اسکالر نیز گفته می شود)، عملی است که دو بردار را به عنوان ورودی می گیرد و یک عدد خروجی می دهد. برای آشنایی شکل کلی این ضرب، ابتدا خوب است کمی با بردارهایی با تعداد مولفه های بیشتر از دو آشنا شویم.

1-58 فضای سه بعدی

برداری که سه مولفه داشته باشد؛ در دستگاه مختصات دکارتی سه بعدی یا $\mathbb{R}^3$ زندگی می کند. بردار دلخواه $\vec{v}$ به صورت زیر تعریف می شود:

(1)

$\large \vec{v}=\begin{bmatrix} v_x \\ v_y \\ v_z \end{bmatrix}=v_x\hat{i}+v_y\hat{j}+v_z\hat{k}$

که $\hat{i}$، $\hat{j}$ و $\hat{k}$ بردارهای پایه، محور $x$، $y$ و $z$ هستند. ترسیم بردارهای سه بعدی بصورت یک عکس کاربردی و زیبا نیست؛ به همین دلیل می توانید از بسته نرم افزاری سه بعدی جئوجبرا بهره ببرید. در بخش input، می توانید دستور زیر را وارد کنید تا بردار $\vec{u}=\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}$ نمایش داده شود:

u= Vector((0,0,0),(1,2,3))

تمامی عملیات ها همچون جمع و تفریق بردارها مشابه بردارهای دوبعدی بصورت مولفه به مولفه امکان پذیر است.

2-58 زوایای هادی

زاویه های هادی، زاویه بین بردار و محورهای مختصات اند. برای بردار دلخواه $\vec{a}=\begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix}$ (شکل 58-1)، مقدار کسینوس زوایای هادی به سادگی از مثلثات قابل دستیابی است:

(2)

$\large \cos{(\alpha)}=\displaystyle{\frac{a_x}{|\vec{a}|}} \; , \; \cos{(\beta)}=\displaystyle{\frac{a_y}{|\vec{a}|}} \; , \; \cos{(\gamma)}=\displaystyle{\frac{a_z}{|\vec{a}|}}$

که $\alpha$، $\beta$ و $\gamma$ به ترتیب زاویه های بین بردار و محور $x$، $y$ و $z$ است.

شکل 58-1، زوایای هادی

می دانیم اندازه یک بردار با سه مولفه بصورت زیر است:

(3)

$\large |\vec{a}|=\sqrt{a^2_x+a^2_y+a^2_z}$

با تقسیم دو طرف تساوی بالا بر $|\vec{a}|$ و استفاده از (2) رابطه مهم زیر برای کسینوس زوایای هادی بدست می آید:

(4)

$\large \cos^2{(\alpha)}+\cos^2{(\beta)}+\cos^2{(\gamma)}=1$

3-58 فضای n بعدی

بردارها اشیائی هستند که به هر میزان دلخواهی (مثل $n$) می توانند مولفه داشته باشند. فضای این بردارها $\mathbb{R}^n$ است. باتوجه به تعداد زیاد مولفه ها و بردارهای پایه، آن ها را با$v_i$ و $\hat{e_i}$ نام گذاری می کنم که $i$ عددی طبیعی است و نشانگر محوری خاص در فضا. بردار دلخواه $\vec{v}$ با $n$ مولفه بصورت زیر است:

(5)

$\large \vec{v}=\displaystyle{\begin{bmatrix} v_1\\v_2 \\ \vdots \\v_n \end{bmatrix}}=v_1\hat{e_1}+v_2\hat{e_2}+…+v_n\hat{e_n}$

متاسفانه چنین بردارهایی بدلیل اینکه می توانند بیش از سه مولفه داشته باشند؛ قابل ترسیم نیستند اما کاربردهای گوناگونی در علوم دارند. جمع، تفریق برداری و همچنین زوایای هادی به ابعاد بالاتر نیز قابل تعمیم است.

4-58 ضرب داخلی

همانطور که در مقدمه ذکر کردم، ضرب داخلی عملی است که دو بردار (با تعداد مولفه های یکسان) را به عنوان ورودی می گیرد و یک عدد خروجی می دهد. رابطه کلی ضرب داخلی به این صورت است که مولفه ها، با پایه یکسان را در یکدیگر ضرب می کند؛ سپس همه جملات را باهم جمع می کند تا یک عدد بدست آید. برای دو بردار دلخواه $\vec{a}$ و $\vec{b}$ که مشابه (5) در فضای $\mathbb{R}^n$ تعریف می شوند، داریم:

(6)

$\large \vec{a}.\vec{b}=(a_1)(b_1)+(a_2)(b_2)+…+(a_n)(b_n)$

می توان گفت که ضرب داخلی در جبر برداری معادل ضرب اعداد در جبر اعداد است. کمی جلوتر اتحادهای جبری مشابه اتحادهایی که قبلا داشتیم را برای بردارها بررسی می کنیم. رابطه ای هندسی نیز برای ضرب داخلی وجود دارد که بسیار پرکاربرد و معادل رابطه (6) است. در صورتی که $\theta$ زاویه بین دو بردار دلخواه $\vec{a}$ و $\vec{b}$ باشد؛ ضرب داخلی با اندازه دو بردار و کسینوس زاویه بین رابطه دارد:

(7)

$\large \vec{a}.\vec{b}=|\vec{a}||\vec{b}|\cos{\theta}$

اثبات

برای اثبات رابطه بالا، برای سادگی فضا را دوبعدی درنظر می گیریم. دو بردار $\vec{a}=\displaystyle{\begin{bmatrix} a_1\\a_2  \end{bmatrix}}$ و $\vec{b}=\displaystyle{\begin{bmatrix} b_1\\b_2  \end{bmatrix}}$ و بردار $\vec{a}-\vec{b}$ به شکل زیر باهم یک مثلث می سازند:

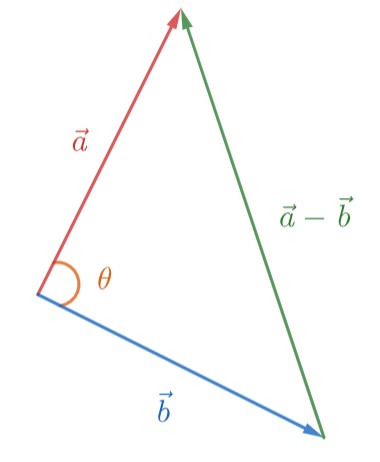
شکل 58-2، مثلث اثبات رابطه (7)

حال از قضیه کسینوس ها که برای مثلث شکل 58-2 برقرار است می دانیم:

(8)

$\large |\vec{a}-\vec{b}|^2=|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}|\cos{\theta}$

از اندازه بردارها (رابطه (3))، جملات رابطه بالا را با نکته سنجی و توجه به رابطه (7) محاسبه می کنیم:

(9)

$\large (a_1 – b_1)^2+(a_2 – b_2)^2=(a^2_1+a^2_2)+(b^2_1+b^2_2)-2|\vec{a}||\vec{b}|\cos{\theta}$

جمله سوم (البته یک دوم آن) خواسته ماست؛ آن را در یک طرف معادله تنها می گذاریم تا حاصل بدست آید:

(10)

$\large 2|\vec{a}||\vec{b}|\cos{\theta}=(a^2_1+a^2_2)+(b^2_1+b^2_2)-(a_1 – b_1)^2-(a_2 – b_2)^2$

که نتیجه می دهد:

(11)

$\large 2|\vec{a}||\vec{b}|\cos{\theta}=2(a_1 b_1+a_2 b_2)$

با ساده کردن $2$ در دو طرف تساوی، رابطه (7) اثبات می شود. ضرب داخلی اطلاعات مهمی در مورد حالت بردارها نسبت به هم می دهد.

1-4-58 حالت عمود

اگر دو بردار دلخواه $\vec{a}$ و $\vec{b}$ برهم عمود باشند، $\cos{\frac{\pi}{2}}=0$ پس ضرب داخلی برابر صفر خواهد بود:

(12)

$\large \vec{a}.\vec{b}=0 \; \Leftrightarrow \; \vec{a}\perp \vec{b} \; , \; \theta=\displaystyle{\frac{\pi}{2}}$

2-4-58 حالت های موازی

اگر دو بردار هم راستا و هم جهت باشند؛ $\cos{0}=1$، پس ضرب داخلی برابر با ضرب اندازه دو بردار خواهد بود:

(13)

$\large \vec{a}.\vec{b}=|\vec{a}||\vec{b}| \; \Leftrightarrow \; \vec{a} \parallel \vec{b}  \; , \; \theta=0 $

اگر دو بردار هم راستا ولی خلاف جهت باشند؛ $\cos{\pi}=-1$، بنابراین ضرب داخلی برابر با قرینه حاصل ضرب اندازه دو بردار است:

(14)

$\large \vec{a}.\vec{b}=-|\vec{a}||\vec{b}| \; \Leftrightarrow \; \vec{a} \parallel \vec{b}  \; , \; \theta=\pi $

*مثال 58-1)

زاویه بین دو بردار $\vec{a}=2\hat{i}+3\hat{j}-1\hat{k}$ و $\vec{b}=-4\hat{i}+\hat{k}$ را محاسبه کنید.

پاسخ

از رابطه (6) حاصل ضرب داخلی را محاسبه می کنیم:

$\large \vec{a}.\vec{b}=(2)(-4)+(3)(0)+(-1)(1)=-9$

اندازه(طول) هر بردار را محاسبه می کنیم تا از رابطه (7) برای محاسبه زاویه بهره ببریم:

$|\vec{a}|=\sqrt{4+9+1}=\sqrt{14} \; , \; |\vec{b}|=\sqrt{16+0+1}=\sqrt{17}$

با کمی تغییر رابطه (7) شکل زیر را به خود می گیرد:

$\theta=\arccos{\displaystyle{(\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|})}}=2.19 \; rad=125.69^\circ$

---

5-58 تصویر بردار بر راستای بردار دیگر

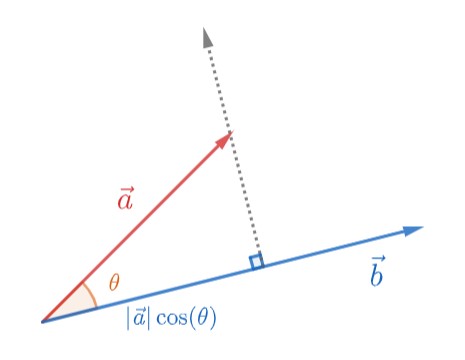
شکل 58-3، تصویر تصویر بردار بر راستای بردار دیگر

برای تصویر بردار $\vec{a}$ بر راستای بردار دیگر $\vec{b}$ (Vector projection)، از نظر هندسی تنها کافی است که از پیکان بردار $\vec{a}$ بر راستای بردار $\vec{b}$ پاره خطی عمود رسم کنیم. مطابق مثلثات، اندازه ضلعی از مثلث قائم الزاویه که در راستای بردار $\vec{b}$ قرار دارد؛ برابر با $|\vec{a}|\cos{(\theta)}$ خواهد بود که $\theta$ زاویه بین دو بردار است. حال تنها کافی است نماینده جهت (یعنی بردار یکه $\hat{b}$) در اندازه تصویر ضرب شود تا بردار تصویر در راستای $\vec{b}$ شکل بگیرد:

(15)

$\large proj_{\vec{b}}{\vec{a}}=|\vec{a}|\cos{(\theta)}\hat{b}$

از طرفی $|\vec{a}|\cos{(\theta)}=\vec{a}.\hat{b}$ (طول بردار یکه، یک است) بنابراین:

(16)

$\large proj_{\vec{b}}{\vec{a}}=(\vec{a}.\hat{b})\hat{b}$

اگر با بردار یکه راحت نیستید؛ می توانید از $\hat{b}=\displaystyle{\frac{\vec{b}}{|\vec{b}|}}$ بردار یکه را جایگذاری کنید:

(17)

$\large proj_{\vec{b}}{\vec{a}}=\displaystyle{\frac{1}{|\vec{b}|^2}}(\vec{a}.\vec{b})\vec{b}$

*مثال 58-2)

بردار تصویر $\vec{a}$ بر راستای بردار $\vec{b}$ را برای بردارهای مثال 58-1 محاسبه کنید.

پاسخ

از رابطه (17) نتیجه دلخواه را بدست می آوریم:

$\large proj_{\vec{b}}{\vec{a}}=\displaystyle{\frac{1}{17}}(-9)\vec{b}=\displaystyle{\frac{36}{17}}\hat{i}-\displaystyle{\frac{9}{17}}\hat{k}$

---

6-58 جمع بندی فصل

در این فصل با بردارهای $n$ مولفه ای، زوایای هادی، ضرب داخلی و تصویر بردار در راستای بردار دیگر آشنا شدیم.

 

تمرینات فصل

*1- کسینوس های هادی بردار زیر را محاسبه کنید.

$\large \vec{u}=\begin{bmatrix} 1 \\ 6 \\ -2 \end{bmatrix}$

*2- رابطه (7) را برای دو بردار با سه مولفه اثبات نمایید. (راهنمایی: روش اثبات تفاوت خاصی ندارد.)

-عبارات زیر را در فضای $\mathbb{R}^3$ثابت کنید:

*3-$\large \vec{a}.(\vec{b}+\vec{c})=\vec{a}.\vec{b}+\vec{a}.\vec{c}$

*4-$\large |\vec{u}|^2=\vec{u}.\vec{u}$

*5-$\large \vec{a}.\vec{b} \leq |\vec{a}||\vec{b}|$

*6- علت نادرستی عبارت زیر را بیان کنید:

$\large \vec{a}.\vec{b}=\vec{a}.\vec{c} \Rightarrow \vec{b}=\vec{c}$

 

ترتیب فصل	قبلی	فعلی	بعدی
عنوان	57 بردار : مقدمه	58 بردار : ضرب داخلی	59 بردار : ضرب خارجی