در علوم تجربی، گاها با کمیت هایی روبه‌رو می شویم که تنها دارای مقدار هستند. به این کمیت ها، کمیت اسکالر یا نرده ای می گوییم. کمیت های فیزیکی مانند جرم و دما اینگونه اند. اما کمیت هایی نیز وجود دارند که علاوه بر مقدار دارای جهت اند؛ مثلا در جابجایی یک جعبه بر روی زمین، اگر بگویم این جعبه $5$ متر جابجا شده؛ اطلاعات کافی را دراختیار شما قرار نداده ام. حتما این سوال برای شما پیش می آید که این انتقال در چه جهتی رخ داده است. پس لازم است بگویم که $5$ متر به سمت چپ. بردارها اینگونه کمیت ها را نمایندگی می کنند و به همین دلیل به جابجایی، نیرو، سرعت و… کمیت برداری می گوییم.

1-57 تعریف

بردارها اشیائی دارای اندازه(بزرگی) و جهت اند. اگر ذره ای داشتیم که تنها در یک بعد حرکت می کرد؛ کافی بود که جهت حرکت آن را مثبت و خلاف آن را منفی در نظر بگیریم (شبیه محور اعداد). اما برای ذراتی که در صفحه حرکت می کنند؛ وضعیت به این سادگی نیست. جابجایی باز در اینجا به من کمک خواهد کرد.

فریدون بوسیله دوچرخه از دانشگاه به سمت خانه حرکت می کند. در مسیر او باید یک کیلومتر به سمت شرق و دو کیلومتر به سمت شمال رکاب بزند تا به خانه برسد:

شکل 57-1، مسیر برگشت فریدون از دانشگاه

چون این جابجایی جهت دار است؛ بوسیله یک بردار آن را توصیف می کنیم. یک محور اعداد در راستای شمالی-جنوبی و یک محور در راستای شرقی-غربی درنظر می گیریم. اگر دو محور در یک مبداء مختصات (مثلا در اینجا مکان دانشگاه) قطع کنند؛ می توان جابجایی فریدون را به صورت زیر در دستگاه مختصات دکارتی نمایش داد:

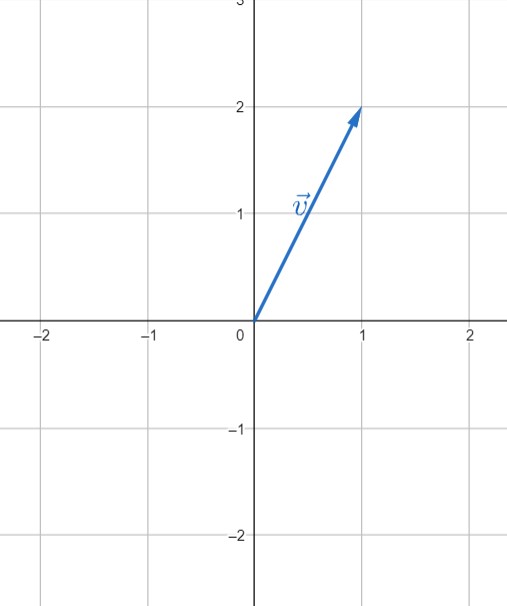
شکل 57-2، بردار جابجایی فریدون $\vec{v}$، جهت شمال $y$ و شرق $x$ را مثبت گرفتم.

یک بردار را معمولا با حرف کوچک لاتین و با علامت مخصوص نمایش می دهیم. علاوه بر نمایش هندسی، نمایش ماتریس بردار نیز حائز اهمیت است. بردار را به صورت ماتریسی ستونی نشان می دهیم که درایه سطر اول، میزان انتقال در جهت محور $x$ و درایه سطر دوم، میزان انتقال در جهت محور $y$ را نشان می دهد:

(1)

$\large \vec{v}=\displaystyle{\begin{bmatrix} v_{x} \\ v_{y} \end{bmatrix}}$

در مثال فریدون، $v_{x}=1$ و $v_{y}=2$ بود($ \vec{v}=\displaystyle{\begin{bmatrix} 1 \\ 2 \end{bmatrix}}$). مسافت طی شده توسط فریدون $3$ کیلومتر بود اما او قطعا کمتر از اینها بر روی زمین جابجا شده است. میزان جابجایی فریدون از قضیه فیثاغورث بدست می آید:

$\large |\vec{v}|=\sqrt{1^2+2^2}=\sqrt{5}$

این همان اندازه بردار جابجایی است؛ پس بطور کلی اندازه یک بردار از قضیه فیثاغورث حاصل می شود؛ چون مولفه های $x$ و $y$ هر بردار همانند اضلاع قائمه مثلث قائم الزاویه و خود بردار وتر این مثلث است:

(2)

$\large |\vec{v}|=\sqrt{v_{x}^2+v_{y}^2}$

2-57 بردار یکه

برداری که اندازه آن یک باشد را بردار یکه می گوییم. از هر برداری می توان یک بردار یکه ساخت؛ تنها کافی است که بردار را بر اندازه خود تقسیم کنیم:

(3)

$\large \hat{v}=\displaystyle{\frac{\vec{v}}{|\vec{v}|}}$

می توان گفت که بردار یکه نشان دهنده از جهت نمایندگی می کند. برای مثال بردار یکه جابجایی فریدون به صورت زیر است:

$\large \hat{v}=\displaystyle{\frac{1}{\sqrt{5}}}\displaystyle{\begin{bmatrix} 1 \\ 2 \end{bmatrix}}$

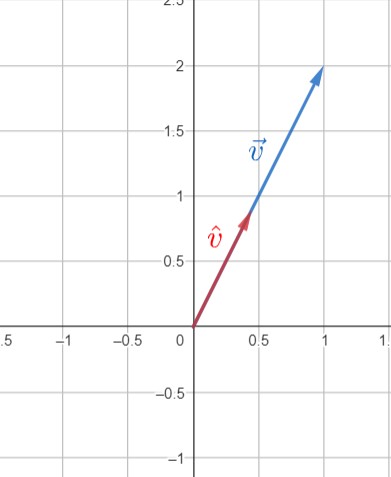
شکل 57-3، بردار یکه $\hat{v}$ جهت بردار $\vec{v}$ را نشان می دهد.

3-57 بردارهای پایه

بردارهای پایه، بردارهایی یکه اند که جهت محورهای اصلی مختصات را نشان می دهند و به همین دلیل برهم عمودند. بردار پایه محور $x$ را با $\hat{i}$ و بردار پایه محور $y$ را با $\hat{j}$ نمایش می دهیم:

(4)

$\large \hat{i}=\displaystyle{\begin{bmatrix} 1 \\ 0 \end{bmatrix}} \; , \; \hat{j}=\displaystyle{\begin{bmatrix} 0 \\ 1 \end{bmatrix}}$

ویژگی بارز بردارهای پایه این است که می توان هربردار در صفحه را می توان به شکل ترکیبی از این دو بردار نشان داد؛ به عنوان یک نمونه برای بردار جابجایی فریدون داریم:

(5)

$\large \vec{v}=\displaystyle{\begin{bmatrix} 1 \\ 2 \end{bmatrix}}=\displaystyle{\begin{bmatrix} 1 \\ 0 \end{bmatrix}}+2\displaystyle{\begin{bmatrix} 0 \\ 1 \end{bmatrix}}=\hat{i}+2\hat{j}$

4-57 قرینه یک بردار

با قرینه سازی مولفه های بردار، بردار قرینه می شود، قرینه بردار رابطه (1) به صورت زیر است:

(6)

$\large -\vec{v}=\displaystyle{\begin{bmatrix} -v_{x} \\ -v_{y} \end{bmatrix}}=-v_{x}\hat{i}-v_{y}\hat{j}$

قرینه هربردار، همانند چرخش $180$ درجه بردار در دستگاه مختصات است.

شکل 57-4، قرینه بردار جابجایی فریدون $-\vec{v}=-\hat{i}-2\hat{j}$

5-57 ضرب عدد در بردار

ضرب یک عدد دلخواه $k$ در بردار همانند ضرب یک عدد در ماتریس ستونی است. ضرب عدد $k$ در بردار $\vec{v}$ طول یا اندازه آن را نیز $k$ برابر می کند.

(7)

$\large k\vec{v}=\displaystyle{\begin{bmatrix} kv_{x} \\ kv_{y} \end{bmatrix}}=kv_{x}\hat{i}+kv_{y}\hat{j}$

قرینه یک بردار، مثالی از ضرب عدد $k=-1$ در بردار است.

6-57 جمع و تفریق برداری

برای جمع یا تفریق دو بردار، کافی است مولفه های آنها را باهم جمع یا از هم کم کنید. برای دو بردار دلخواه $\vec{v}$ و $\vec{w}$ داریم:

(8)

$ \vec{v}+\vec{w}=\displaystyle{\begin{bmatrix} v_x+w_x \\ v_y+w_y \end{bmatrix}}=(v_x+w_x)\hat{i}+(v_y+w_y)\hat{j}$

(9)

$\vec{v}-\vec{w}=\displaystyle{\begin{bmatrix} v_x-w_x \\ v_y-w_y \end{bmatrix}}=(v_x-w_x)\hat{i}+(v_y-w_y)\hat{j}$

از رابطه (8) واضح است که جمع دو بردار جابجایی پذیر است.

*مثال 57-1)

با استفاده از اطلاعات زیر، عبارت $\hat{a}-\hat{b}$ و حاصل را به شکل ترکیبی از بردارهای پایه بنویسید.

$\large \vec{a}=\displaystyle{\begin{bmatrix} -1 \\ 3 \end{bmatrix}} \; , \; \vec{b}=\displaystyle{\begin{bmatrix} 0 \\ 2 \end{bmatrix}}$

پاسخ

ابتدا بردار های یکه $\hat{a}$ و $\hat{b}$ را از رابطه (3) بدست می آوریم:

$ \hat{a}=\displaystyle{\frac{1}{\sqrt{(-1)^2+(3)^2}}}\displaystyle{\begin{bmatrix} -1 \\ 3 \end{bmatrix}}=-\displaystyle{\frac{1}{\sqrt{10}}}\hat{i}+\displaystyle{\frac{3}{\sqrt{10}}}\hat{j}$

$ \hat{b}=\displaystyle{\frac{1}{\sqrt{(0)^2+(2)^2}}}\displaystyle{\begin{bmatrix} 0 \\ 2\end{bmatrix}}=\hat{j}$

البته واضح بود که چون $b$ تنها مولفه $y$ با علامت مثبت دارد پس بردار یکه آن $\hat{j}$ خواهد بود. حال مولفه های دو بردار را ازهم کم می کنم:

$ \hat{a}-\hat{b}=-\displaystyle{\frac{1}{\sqrt{10}}}\hat{i}+\displaystyle{\frac{3-\sqrt{10}}{\sqrt{10}}}\hat{j}$

---

7-57 تصویر بردار بر روی محورها (محاسبه مولفه)

برای یک بردار، طول آن و زاویه ای که با محور $x$ دارد نیز حاوی تمامی اطلاعات بردار از جمله مولفه های آن است. برای بردار دلخواه $\vec{v}$ که زاویه تند (کوچکتر از $90$ درجه) $\theta$ با محور $x$ دارد؛ مولفه ها(تصویر بردار برروی محورها) به صورت زیر محاسبه می شوند:

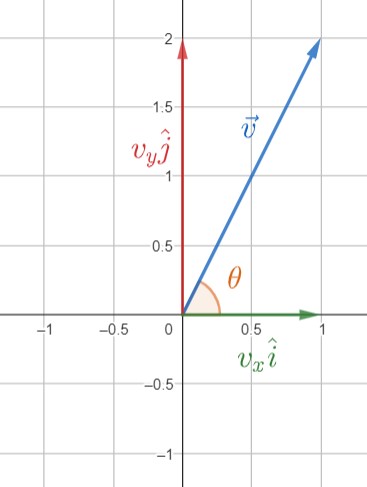
شکل 57-5، بردار $\vec{v}$ و زاویه $\theta$

از مثلث قائم الزاویه و روابط مثلثاتی حاکم بر آن می دانیم:

(10)

$\large \cos{(\theta)}=\displaystyle{\frac{v_x}{|\vec{v}|}} \; , \; \sin{(\theta)}=\displaystyle{\frac{v_y}{|\vec{v}|}}$

 

بنابراین مولفه های بردار، با توجه به اندازه بردار و زاویه آن با محور $x$ به شکل زیر بدست می آیند:

(11)

$\large v_x=|\vec{v}|\cos{(\theta)} \; , \; v_y=|\vec{v}|\sin{(\theta)}$

خوشبختانه مثلثات اجازه می دهد رابطه بالا را برای هر $\theta$ تند، قائم و باز محاسبه کنیم اما دقت کنید که همیشه بنابر قرارداد $\theta$ زاویه ای است که از جهت مثبت $x$ به صورت پادساعتگرد حرکت می کند تا به بردار برسد. فقط با این شرط است که محاسبه همیشه درست خواهد بود.

*مثال 57-2)

مولفه های بردار $\vec{k}$ و خود بردار را با اطلاعات زیر رسم کنید.

$\large |\vec{k}|=2 \; , \; \theta=\displaystyle{\frac{7\pi}{6}\: rad}$

پاسخ

از (11) مولفه های بردار را حساب می کنم:

$ k_x=(2)(\cos{(\frac{7\pi}{6})}=(2)(-\frac{\sqrt{3}}{2})=-\sqrt{3}$

$k_y=(2)(\sin{(\frac{7\pi}{6})}=(2)(-\frac{1}{2})=-1$

بدین ترتیب $\vec{k}$ به صورت زیر است:

$\large k=-3\hat{i}-\hat{j}$

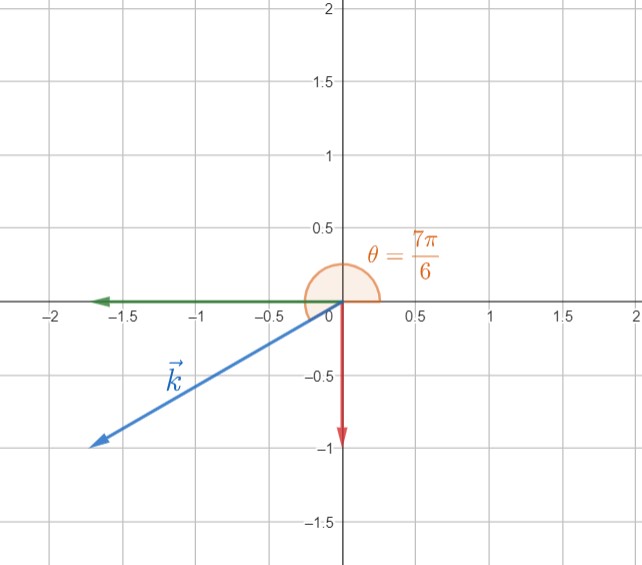
شکل 57-6، مثال 57-2

---

8-57 جمع بندی فصل

با مقدماتی از بردار، نحوه جمع و تفریق آنها، بردار یکه، بردارهای پایه و محاسبه مولفه ها آشنا شدیم. در ادامه تمریناتی برای گرم شدن شما در این مباحث این فصل می آورم. امید است که مفید واقع شود.

 

تمرینات فصل

*1- بردارهای زیر را درنظر بگیرید و خواسته ها را انجام دهید:

$\large \vec{a}=2\hat{i}+3\hat{j} \; , \; \vec{b}=-2\hat{i}+\hat{j}$

$\large 3\vec{a}-2\vec{b}\; , \; 4\hat{a}+\vec{b} \; , \; \hat{b} $

*2- بردار صفر برداری است که هیچ مولفه ای ندارد:

(12)

$\large \vec{o}=0\hat{i}+0\hat{j}$

با استفاده از رابطه (1) و (6) نشان دهید:

(13)

$\large \vec{v}+(-\vec{v})=\vec{o}$

*3- با درنظر گرفتن اولویت پرانتز و جمع مولفه ها، برای سه بردار دلخواه $a$ و $b$ و $c$ ثابت کنید:

(14)

$a+(b+c)=(a+b)+c=a+b+c$

*4- مولفه های بردار $\vec{l}$ و $\hat{l}$ با مشخصات زیر را بدست آورید:

$\large |\vec{l}|=2 \; , \; \theta=120^{\circ}$

 

ترتیب فصل	قبلی	فعلی	بعدی
عنوان	56 ماتریس : ماتریس وارون	57 بردار : مقدمه	58 بردار : ضرب داخلی