در فصل قبل با ضرب داخلی آشنا شدیم. ضرب خارجی عملی است که دو بردار سه مولفه ای را به عنوان ورودی می گیرد و یک بردار، عمود برهردو بردار ورودی را خروجی می دهد. ضرب خارجی در فیزیک الکترومغناطیس کاربرد بسزایی دارد.

1-59 تعریف

دو بردار دلخواه$\vec{a}=\begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix}$ و $\vec{b}=\begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}$ را در نظر بگیرید. ضرب خارجی این دو بردار را با نماد $\vec{a} \times \vec{b}$ به صورت دترمینان زیر تعریف می کنیم:

(1)

$\large \vec{a} \times \vec{b}=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}=(a_2b_3-a_3b_2)\hat{i}+(a_3b_1-a_1b_3)\hat{j}+(a_1b_2-a_2b_1)\hat{k}$

توجه کنید که جابجایی سطر دوم و سوم دترمینان سبب قرینه شدن حاصل می شود. بنابراین جابجایی دو بردار به اندازه یک منفی هزینه دارد:

(2)

$\large \vec{a}\times \vec{b}=-\vec{b}\times \vec{a}$

2-59 طول بردار حاصل ضرب خارجی

محاسبه اندازه یا طول بردار حاصل ضرب خارجی کار دشواری نیست؛ اگر $\theta$ زاویه بین دو بردار $\vec{a}$ و $\vec{b}$ باشد داریم:

$\large |\vec{a}\times\vec{b}|^2=(a_2b_3-a_3b_2)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2$

با حوصله جملات را به توان دو می رسانیم:

$\large =a^2_2b^2_3+a^2_3b^2_2-2a_2a_3b_2b_3+a^2_3b^2_1+a^2_1b^2_3-2a_1a_3b_1b_3+a^2_1b^2_2+a^2_2b^2_1-2a_1a_2b_1b_2$

اگر در عبارت بالا دقت کنیم؛ به این پی می بریم که جملاتی از جنس $a^2_ib^2_i$ وجود ندارد ($i=1,2,3$). بنابراین می توان عبارت زیر را به عنوان حاصل بالا درنظر داشت:

$\large =(a^2_1+a^2_2+a^2_3)(b^2_1+b^2_2+b^2_3)-(a_1 b_1+a_2 b_2+a_3 b_3)^2$

در جمله اول طول دو بردار به توان دو در هم ضرب شده و جمله دوم، ضرب داخلی دو بردار به توان دو رسیده پس:

$\large =(|\vec{a}||\vec{b}|)^2-(\vec{a}.\vec{b})^2=(|\vec{a}||\vec{b}|)^2-(|\vec{a}||\vec{b}|)^2 \cos^2{(\theta)}$

فاکتورگیری و رابطه مثلثاتی سینوس و کسینوس، جواب را بدست می دهد:

$\large |\vec{a}\times\vec{b}|^2=(|\vec{a}||\vec{b}|)^2(1-\cos^2{(\theta)})=|\vec{a}|^2|\vec{b}|^2\sin^2{(\theta)}$

بدین ترتیب طول بردار حاصل ضرب خارجی از رابطه زیر قابل محاسبه است:

(3)

$\large |\vec{a}\times\vec{b}|=|\vec{a}||\vec{b}|\sin{(\theta)}$

بنابر رابطه (3)، اگر دو بردار هم راستا (موازی) باشند؛ حاصل ضرب خارجی آنها بردار صفر است. اگر دو بردار برهم عمود باشند؛ طول بردار ضرب خارجی حاصل برابر با حاصل ضرب طول دو بردار است. از دیدگاه هندسی، اندازه بردار ضرب خارجی، مساحت متوازی الاضلاعی به ضلع $|\vec{a}|$ و $|\vec{b}|$ است.

شکل 59-1، مساحت متوازی الاضلاع با اضلاع $|\vec{a}|$ و $|\vec{b}|$ از رابطه (3) بدست می آید.

*مثال 59-1)

ضرب خارجی بردار $\vec{a}=\begin{bmatrix} 1 \\ 2 \\ 2 \end{bmatrix}$ در $\vec{b}=\begin{bmatrix} 0 \\ -1 \\ 3 \end{bmatrix}$ را بدست آورید.

پاسخ

از رابطه (1) استفاده می کنیم:

$\large \vec{a} \times \vec{b} = [(2)(3)-(2)(-1))]\hat{i}+[(2)(0)-(1)(3)]\hat{j}+[(1)(-1)-(2)(0)]\hat{k}=8\hat{i}-3\hat{j}-\hat{k}$

---

3-59 ضرب خارجی بردارهای پایه

ضرب خارجی سه بردار پایه فضا یعنی $\hat{i}$،$\hat{j}$ و $\hat{k}$ از این جهت مهم است که حاصل ضرب خارجی هردو بردار پایه، بردار پایه دیگر یا قرینه آن است. برای مثال:

$\large \hat{i}\times\hat{j}=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{vmatrix}=\hat{k}$

$\large \hat{k}\times\hat{j}=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{vmatrix}=-\hat{i}$

بنابراین حاصل ضرب ها را می توان بوسیله گردونه زیر به خاطر سپرد؛ ضرب خارجی در جهت چرخش، علامت مثبت و ضرب خارجی در خلاف جهت، علامت منفی را نتیجه می دهد.

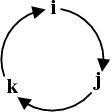
شکل 59-2، گردونه ضرب خارجی بردارهای پایه

4-59 حجم متوازی السطوح

متوازی السطوح حجمی با شش وجه است که هروجه آن متوازی الاضلاع است(وجه های روبرو مساحت و اضلاع یکسان دارند). یکی از کاربردهای ضرب خارجی و دترمینان، محاسبه حجم این شکل سه بعدی است. مطابق شکل 59-3، فرض کنید متوازی السطوحی به وسیله سه بردار $\vec{a}$، $\vec{b}$ و $\vec{c}$ ساخته شده است.

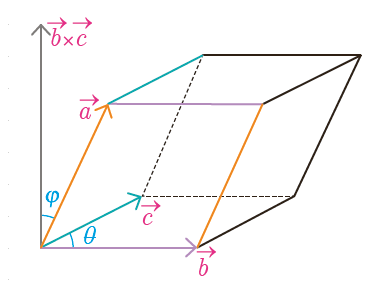
شکل 59-3، متوازی السطوح ساخته شده با سه بردار $\vec{a}$، $\vec{b}$ و $\vec{c}$

حجم متوازی السطوح با قاعده $A$ و ارتفاع $h$ از رابطه زیر قابل محاسبه است:

(4)

$\large V=Ah$

برای محاسبه حجم، ما قاعده $A=|\vec{b}\times \vec{c}|$ را انتخاب می کنیم. ارتفاع عمود بر صفحه قاعده است؛ پس تصویر $\vec{a}$ بر $\vec{b} \times \vec{c}$ بردار ارتفاع را می دهد که اندازه آن از رابطه زیر قابل محاسبه است (در فصل 58 به تصویر بردار بر راستای بردار دیگر پرداختیم):

(5)

$\large h=\displaystyle{\frac{\vec{a}.(\vec{b}\times \vec{c})}{|\vec{b}\times \vec{c}|}}$

بدین ترتیب بنابر رابطه (4) حجم متوازی السطوح بدست می آید (حجم را به عنوان یک کمیت مثبت فرض می کنیم و یک قدرمطلق نیز برای پاسخ نهایی درنظر می گیریم):

(6)

$\large V=|\vec{a}.(\vec{b}\times \vec{c})|$

رابطه بالا از طریق قدرمطلق دترمینان زیر به سهولت قابل محاسبه است:

(7)

$\large K=\begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix} \rightarrow V=|K|$

یکی از کمک هایی که مسئله حجم متوازی الاسطوح می کند؛ برابری ضرب های سه گانه است:

(8)

$\large \vec{a}.(\vec{b}\times \vec{c})=\vec{b}.(\vec{c}\times \vec{a})=\vec{c}.(\vec{a}\times \vec{b})$

برهان ساده ای که می توان برای اثبات رابطه بالا به کار برد این است که برای ساخت هرکدام از ضرب های سه گانه، همیشه به تعداد زوج جای سطرهای دترمینان رابطه (7) را تعویض کنیم، بنابراین علامت دترمینان تفاوتی نمی کند و حاصل یکسان است.

5-59 جمع بندی فصل

در این فصل با ضرب خارجی آشنا شدیم. بار دیگر توجهتان را به این مهم جلب می کنم که ضرب خارجی فقط برای بردارهای سه مولفه ای تعریف می شود اما ضرب داخلی عملی برای همه بردارها برقرار است. محاسبه مساحت مثلث، متوازی الاضلاع و مساحت جانبی متوازی الاسطوح نیز با مطالب این فصل امکان پذیر است.

 

تمرینات فصل

– خواص زیر را اثبات نمایید:

*1- $\large \vec{a}\times (\vec{b}+\vec{c})=\vec{a}\times \vec{b} + \vec{a}\times \vec{c}$

*2- $\large (\vec{b}+\vec{c})\times \vec{a}=\vec{b}\times \vec{a} + \vec{c}\times \vec{a}$

*3- اگر $r$ یک عدد حقیقی باشد:

$\large (r\vec{a})\times \vec{b}=\vec{a}\times (r\vec{b})= r(\vec{a} \times \vec{b})$

*4- برداری یکه، عمود بر $\vec{a}=\hat{i}-3\hat{j}+2\hat{k}$ و $\vec{b}=-2\hat{i}+1\hat{j}-5\hat{k}$ بیابید.

 

ترتیب فصل	قبلی	فعلی	بعدی
عنوان	58 بردار : ضرب داخلی	59 بردار : ضرب خارجی	60 صفحه در فضای سه بعدی