صفحه شکلی دوبعدی است که می خواهیم آن را در فضای سه بعدی بررسی کنیم و معادله صفحه را بدست آوریم. نقطه $P=(x,y,z)$ را در نظر بگیرید. یک معادله با سه متغیر $x$،$y$ و $z$ قیدی بر روی نقطه می گذارد که آزادانه نمی تواند در هرجای فضای سه بعدی قرار بگیرد. برای مثال معادله ساده زیر را در نظر بگیرید:

$\large x+y+z=2 \rightarrow z=2-x-y$

این همان قید است که یک درجه آزادی را از نقطه $P$ می گیرد و آن را وادار می سازد که بر سطحی دوبعدی (یا گاها با ابعاد کمتر) قرار گیرد.

1-60 تعریف

شکل 60-1 را در نظر بگیرید؛ نقطه $P_0$ در فضای $\mathbb{R}^3$ با بردار موقعیت زیر مشخص می شود:

(1)

$\large \vec{r_{0}}=x_{0}\hat{i}+y_{0}\hat{j}+z_{0}\hat{k}$

بردار دلخواه غیرصفر $\vec{n}=A\hat{i}+B\hat{j}+C\hat{k}$ را هم داریم. در این صورت فقط و فقط یک صفحه وجود دارد که از $P_0$ می گذرد و بر بردار $\vec{n}$ عمود است. حال اگر $P$ با بردار موقعیت $\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$ نماینده نقاط روی صفحه باشد. هر بردار نوعی $\overrightarrow{P_0P}=\vec{r}-\vec{r_0}$ نیز با توجه به اینکه مطابق شکل 60-1، در صفحه واقع است؛ بر $\vec{n}$ عمود است. بنابراین ضرب داخلی این دو بردار صفر است. همین برای ما معادله صفحه را می سازد:

(2)

$\large \vec{n}.(\vec{r}-\vec{r_0})=0$

این معادله را فرم برداری معادله صفحه می گویند.

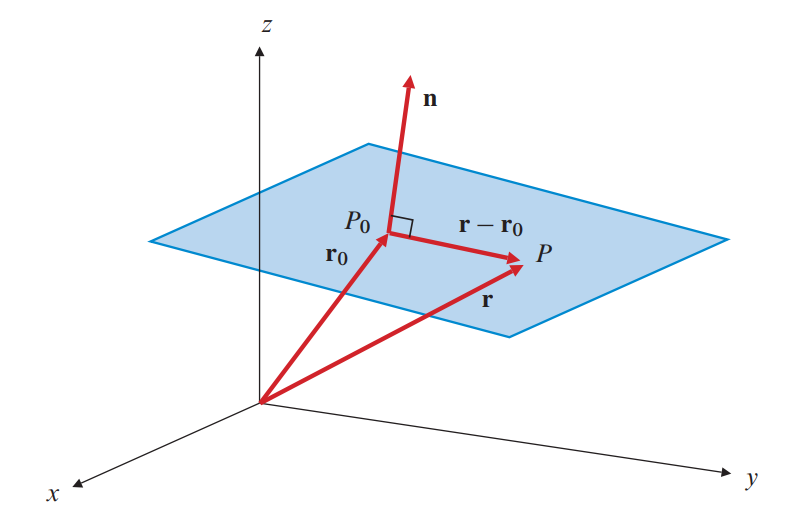
شکل 60-1، یک صفحه در فضای سه بعدی با یک بردار نرمال $\vec{n}$ گذرنده از نقطه $P_0$

با استفاده از تعاریفی که برای بردارها و مختصات کردیم، می توانیم معادله (2) را از حالت بردار خارجی کنیم:

(3)

$\large A(x-x_0)+B(y-y_0)+C(z-z_0)=0$

این فرم اسکالر معادله صفحه را می توان به شکلی مشهور درآورد. با درنظر گرفتن $Ax_0+By_0+Cz_0=D$ ؛ فرم استاندارد معادله صفحه برقرار می شود:

(4)

$\large Ax+By+Cz=D$

برای مثال، در صورتی که بردار نرمال سه مولفه غیرصفر داشته باشد. می توان از رابطه بالا تضمین کرد که صفحه از سه نقطه زیر می گذرد (کافی است نقاط را جایگذاری کنید).

$\large (\displaystyle{\frac{D}{A}},0,0) \; , \; (0,\displaystyle{\frac{D}{B}},0) \; , \; (0,0,\displaystyle{\frac{D}{C}})$

مطابق بالا، اگر $D=0$ باشد؛ صفحه باید از مبداء مختصات عبور کند.

*مثال 60-1)

معادله صفحه گذرنده از سه نقطه $(1,1,0)$، $(2,0,2)$ و $(0,3,3)$ را بیابید.

پاسخ

کافی است ضرب خارجی دو بردار خارجی داخل صفحه را بدست آوریم. با توجه به اینکه بردار حاصل، بر بردارهای داخل صفحه عمود است؛ بردار نرمال خواهد بود. بردارهای انتخابی بردار های واصل انتخابی از تفریق مختصات نقاط بصورت زیر است:

$\large \vec{a}=\hat{i}-\hat{j}+2\hat{k} \; , \; \vec{b}=-\hat{i}+2\hat{j}+3\hat{k}$

بردار نرمال حاصل ضرب خارجی دو بردار است:

$\large \vec{n}=\vec{a} \times \vec{b}=\displaystyle{\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -1 & 2 \\ -1 & 2 & 3 \end{vmatrix}}=-7\hat{i}-5\hat{j}+\hat{k}$

حال کافی است فرم استاندارد یا رابطه (4) را با یکی از نقاط جایگذاری کنیم تا $D$ بدست آید:

$\large (-7)(1)+(-5)(1)+(1)(0)=D \rightarrow D=-12$

بنابراین معادله صفحه بصورت روبرو است:

$\large -7x-5y+z=-12$

---

2-60 خانواده صفحه

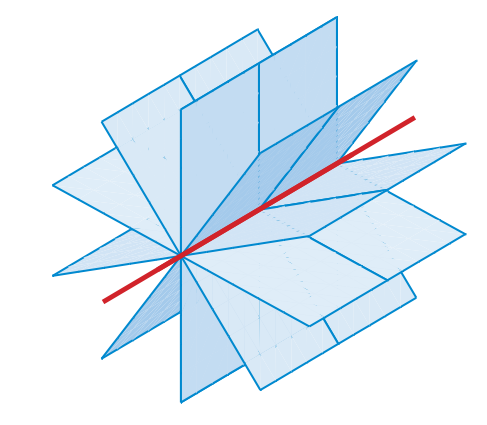
شکل 60-2، یک خانواده صفحه

دسته صفحاتی که همگی در یک خط راست مشترک و متقاطع باشند(شکل 60-2)، یک خانواده صفحه (Pencil of Planes) نامیده می شوند. اگر معادله دو صفحه غیرموازی از یک خانواده را داشته باشیم:

(5)

$\large A_1x+B_1y+C_1z-D_1=0 \; , \; A_2x+B_2y+C_2z-D_2=0$

در این صورت به ازای هر مقدار دلخواه $\lambda$، معادله زیر، معرف یک صفحه از این خانواده خواهد بود:

(6)

$\large (A_1x+B_1y+C_1z-D_1)+\lambda(A_2x+B_2y+C_2z-D_2)=0$

واضح است که $x$،$y$ و $z$ در معادلات (5) صدق می کنند؛ با صفر کردن پرانتزها، به ازای هر $\lambda$ در رابطه بالا نیز صادق اند. توجه کنید که با انتخاب $\lambda$ مناسب، هرصفحه از این خانواده را می توان به دست آورد (البته به جز $A_2x+B_2y+C_2z-D_2=0$). یک مثال نحوه به کاربستن رابطه (6) را روشن می سازد.

*مثال 60-2)

معادله صفحه گذرنده از خط تقاطع دو صفحه $2x+3y=z$ و $x-4y+2z=-5$ و همچنین نقطه $(-2,0,-1)$ را بیابید.

پاسخ

معادله (6) را تشکیل می دهیم:

$\large (2x+3y-z)+\lambda(x-4y+2z+5)=0$

سپس مختصات نقطه را در معادله بالا قرار می دهیم تا $\lambda$ مناسب بدست آید:

$\large (-4+0+1)+\lambda(-2+0-2+5)=0 \rightarrow \lambda=3$

حال معادله (6) با $\lambda$ بدست آمده، رابطه صفحه را می دهد:

$\large 5x-9y+5z=-15$

---

3-60 جمع بندی فصل

با مفهوم صفحه و خانواده صفحه در فضای سه بعدی آشنا شدیم. همچنین معادلات مربوط به صفحه را بدست آوردیم. یک راه خوب برای ترسیم سه بعدی صفحات که نقش شایان توجهی در یادگیری این مبحث دارد؛ استفاده از بسته های نرم افزاری است. در این زمینه من ماشین حساب سه بعدی جئوجبرا را پیشنهاد می دهم. در بخش Input… می توانید معادله را وارد و شکل مدنظر را تماشا کنید.

 

تمرینات فصل

*1- دو صفحه $x-y=3$ و $x+y+z=0$ یکدیگر را قطع می کنند؛ برداری را بیابید که با خط تقاطع موازی باشد.(راهنمایی: این بردار باید بر هردو بردار نرمال عمود باشد)

*2- معادله صفحه ای را بنویسید که از مبداء مختصات عبور می کند و بردار نرمال آن $ \vec{n}=\hat{i}-\hat{j}+2\hat{k}$ است.

 

ترتیب فصل	قبلی	فعلی	بعدی
عنوان	59 بردار : ضرب خارجی	60 صفحه در فضای سه بعدی	61 خط در فضای سه بعدی