از کنار هم قرار گرفتن نقاط در فضای $\mathbb{R}^3$ ، خط تشکیل می شود. همانطور که در فصل قبل دیدیم؛ محل برخورد دو صفحه غیرموازی با یکدیگر، یک خط است. بردار موازی با این خط را می توان از ضرب خارجی بردارهای نرمال دو صفحه بدست آورد. در این فصل به خط و معادله آن در سه بعد می پردازیم.

1-61 تعریف

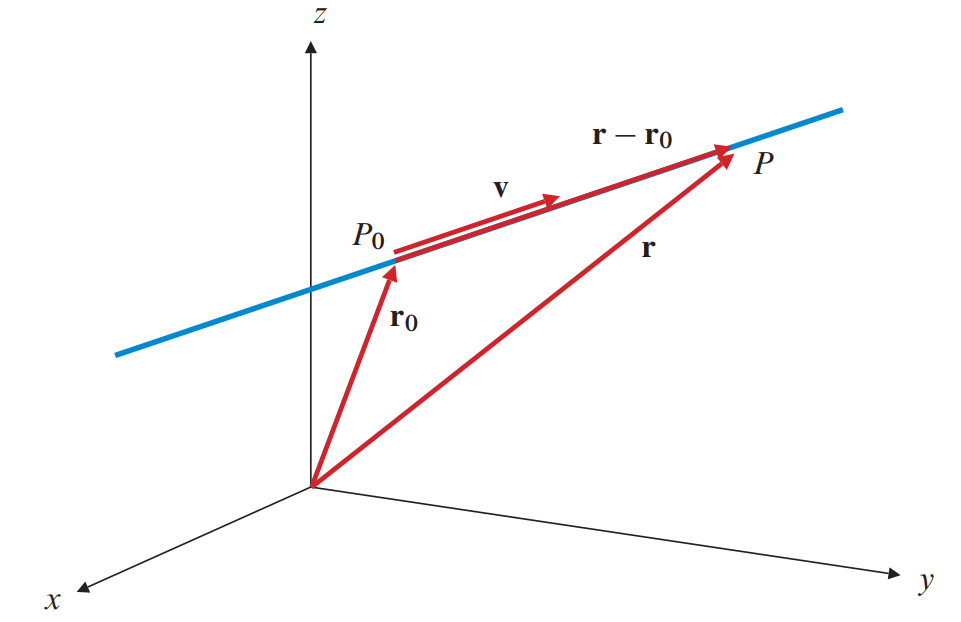
شکل 61-1، خط گذرنده از $P_0$ و بردار $\vec{v}$ که با خط موازی است.

مطابق شکل 61-1، فرض کنید $\vec{r_0}=x_0\hat{i}+y_0\hat{j}+z_0\hat{k}$ بردار موقعیت نقطه $P_0$ است و $\vec{v}=a\hat{i}+b\hat{j}+c\hat{k}$ برداری غیرصفر است. همیشه یک خط منحصر به فرد وجود دارد که از $P_0$ عبور می کند و با بردار $\vec{v}$ موازی است. حال فرض کنید نقطه دلخواه $P$ بر روی این خط را با بردار موقعیت $\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$ نشان دهیم. با توجه به اینکه $\vec{r}-\vec{r_0}$، بر روی خط مورد نظر قرار می گیرد؛ می توان به ازای هر عدد حقیقی $t$ (که صرفا اندازه بردار $\vec{v}$ را با یک ضریب تنظیم می کند تا برابر با تفاضل دو بردار موقعیت شود) معادله زیر را برای خط نوشت:

(1)

$\large \vec{r}-\vec{r_0}=t\vec{v}$

با توجه به اینکه معمولا مختصات نقطه دلخواه $P$ برای ما مجهول است؛ خوب است که رابطه بالا را به شکل زیر بازنویسی کنیم:

(2)

$\large \vec{r}=\vec{r_0}+t\vec{v}$

معادله (2)، معادله پارامتری بردار خط راست نامیده می شود. بردار موقعیت کلیه نقاط با تغییر پارامتر $t$ از $-\infty$ تا $\infty$ قابل محاسبه است. همچنین بردار $\vec{v}$ را بردار هادی خط می نامیم. بردار هادی نمایانگر جهت خط راست است.

با تجزیه مولفه به مولفه بردارهای رابطه (2) و برابری آنها، می توان معادلات پارامتری اسکالر خط را نیز بدست آورد:

(3)

$\large \displaystyle{\left\{\begin{matrix}x=x_0+at\\ y=y_0+bt\\z=z_0+ct \end{matrix}\right.}$

اگر تمامی مولفه های بردار هادی $\vec{v}$ غیرصفر باشند؛ می توان معادلات بالا را برای پارامتر $t$ حل نمود و تساوی زیر را بدست آورد:

(4)

$\large \displaystyle{\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}}$

رابطه بالا را شکل استاندارد معادلات خط راست می دانیم که گذرنده از $P_0$ است و بردار هادی آن، بردار $\vec{v}$ است. در صورتی که یکی از مولفه های بردارهادی صفر باشد (مثلا $c$)، معادله شکل استاندارد به دو تساوی تبدیل می شود:
(5)

$\large \displaystyle{\frac{x-x_0}{a}=\frac{y-y_0}{b}\; , \; z=z_0}$

توجه کنید که معادله خط های راست منحصر به فرد نیستند و به انتخاب یک نقطه خاص $P_0$ روی خط وابسته اند. بنابراین در مسائل گوناگون می توان معادلات مختلفی را برای یک خط راست بدست آورد. درحالت کلی نیز همواره می توان از معادله دو صفحه موازی بهره برد و خط تقاطع آنها را نمایش داد.

*مثال 61-1)

معادلات اسکالر و شکل استاندارد معادلات خط راستی که از نقطه $(1,2,5)$ عبور می کند و با بردار $\vec{v}=\hat{i}-2\hat{k}$ هم جهت است را بیابید.

پاسخ

بردار $\vec{v}$ بردارهادی خط است؛ بنابراین می توان از معادلات (3)، روابط اسکالر خط راست را بدست آورد:

$\large \displaystyle{\left\{\begin{matrix}x=1+t\\ y=2\\z=5-2t \end{matrix}\right.}$

به سادگی شکل استاندارد نیز به طریق مشابه رابطه (5) محاسبه می شود:

$\large \displaystyle{x-1=\frac{z-5}{-2}\; , \; y=2}$

*مثال 61-2)

معادلات خط در شکل استاندارد را برای تقاطع دو صفحه $x+y-z=0$ و $y+2z=6$ بدست آورید.

پاسخ

برای بدست آوردن بردار هادی خط، کافی است بردارهای نرمال دو صفحه را در هم ضرب خارجی کنیم:

$\large \vec{v}=\vec{n_1}\times\vec{n_2}=3\hat{i}-2\hat{j}+\hat{k}$

حال برای تشکیل خط، باید نقطه ای را بیابیم که در هردو معادله صفحه صدق کند(زیرا در تقاطع دو صفحه است)؛ در صورتی که $z=0$ نتیجه می گیریم که $y=6$ و $x=-6$. حال با توجه به اینکه هم نقطه دلخواه و هم بردارهادی را داریم؛ می توانیم شکل استاندارد را تشکیل دهیم:

$\large \displaystyle{\frac{x+6}{3}=\frac{y-6}{-2}=z}$

این نکته شایسته توجه است که رابطه بالا منحصر به فرد نیست. می شد نقطه دلخواه دیگری را پیدا کرد یا حتی بردارهادی را از تفریق دو نقطه دلخواه روی خط بدست آورد.

*مثال 61-3)

معادله پارامتری بردار خط گذرنده از $(-1,0,1)$ و عمود بر صفحه $2x-y+7z=12$ را بیابید.

پاسخ

با توجه به اینکه بردار نرمال همواره بر صفحه عمود است؛ می توان بردار نرمال را به عنوان بردار هادی خط مدنظر انتخاب کرد:

$\large \vec{v}=2\hat{i}-\hat{j}+7\hat{k}$

حال که بردار موقعیت نقطه $(-1,0,1)$ و بردار هادی را داریم؛ از رابطه (2)، معادله پارامتری بردار خط را می نویسیم:

$\large \vec{r}=(-1+2t)\hat{i}-t\hat{j}+(1+7t)\hat{k}$

2-61 جمع بندی فصل

با خط در فضای سه بعدی آشنا شدیم. همچنین روابط معادل برداری، اسکالر و شکل استاندارد را نیز محاسبه کردیم. برای شبیه سازی سه بعدی، می توان از ماشین حساب سه بعدی جئوجبرا استفاده کرد. کافی است در بخش Input… شکل استاندارد خط راست را وارد نمایید.

*1- در متن ذکر کردم که می توان یک خط را بوسیله دو صفحه نشان داد. شکل استاندارد خط زیر را بیابید.

$\large \displaystyle{\left\{\begin{matrix}x-2y+3z=0 \\ 2x+3y-4z=4 \end{matrix}\right.}$