
74 تبدیل های یکانی
در فصل 72 با عملگرهای یکانی آشنا شدیم. در این فصل، به چگونگی تبدیل اسکالرها، کت ها، براها و عملگرها تحت تبدیلات یکانی می پردازیم.

در فصل 72 با عملگرهای یکانی آشنا شدیم. در این فصل، به چگونگی تبدیل اسکالرها، کت ها، براها و عملگرها تحت تبدیلات یکانی می پردازیم.

در فصول قبل عملگرها، حالت ها و ویژگی های آن ها را بررسی نمودیم. بحث این فصل درباره چگونگی یافتن ویژه مقدار ها (Eigenvalues) و

در این فصل به وارون یک عملگر کوانتومی و عملگرهای یکانی می پردازیم. 1-72 وارون یک عملگر در صورتی که عملگر وارون پذیر باشد (همانند

در این فصل به بررسی توابع عملگرهای کوانتومی می پردازیم. 1-71 تعریف فرض کنید که $F(\hat{A})$ تابعی از عملگر $\hat{A}$ باشد. در صورتی که $\hat{A}$
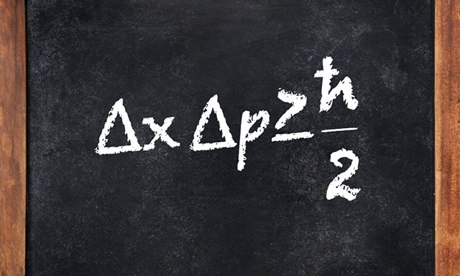
از کاربردهای جبر جابجاگر، محاسبه رابطه کلی برای حاصل ضرب عدم قطعیت های دو عملگر دلخواه است. رابطه ای که روابط عدم قطعیت هایزنبرگ را

در این فصل به جبر جابجاگر (Commutator Algebra) می پردازیم. 1-69 تعریف جابجاگر دو عملگر $\hat{A}$ و $\hat{B}$ با $[\hat{A},\hat{B}]$ نمایش داده می شود. جابجاگر به
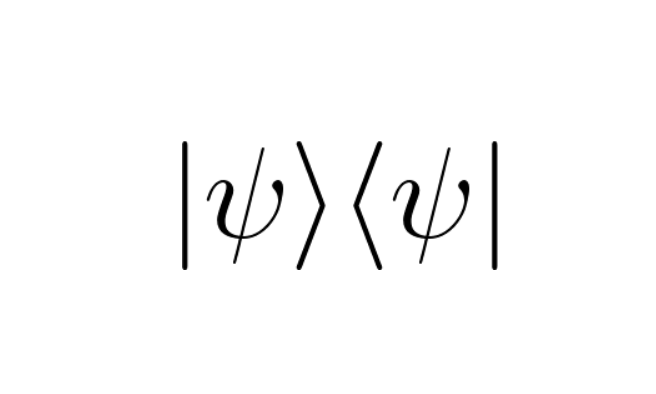
1-68 تعریف عملگر تصویر (projection operator)، عملگری هرمیتی است که با مجذور (مربع) خود برابر است. دو شرط زیر به طور کامل عملگر تصویر $\hat{P}$
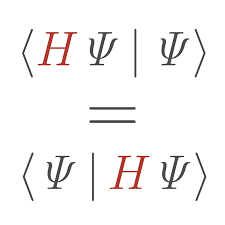
الحاقی هرمیتی یا مزدوج هرمیتی (Hermitian adjoint or conjugate) عملگر، موضوع بحث من در این فصل است. 1-67 تعریف الحاقی هرمیتی هر چیز را با
یکی از مفاهیم بنیادی در صورت بندی مکانیک کوانتومی، عملگر است. در این فصل با تعریف عملگر و چند عملگر خاص که در مکانیک کوانتوم

حالت فیزیکی یک سامانه کوانتومی، با عنصرهای فضای هیلبرت نمایش می دهیم. این عناصر، بردارهای حالت نامیده می شوند. بردارهای حالت در پایه های متفاوت

توابع انتگرال پذیر مجذوری و ضرب داخلی در فضای توابع، بحث این فصل است. در فضای توابع، بردارها با تابع مختلط و ضرب داخلی با
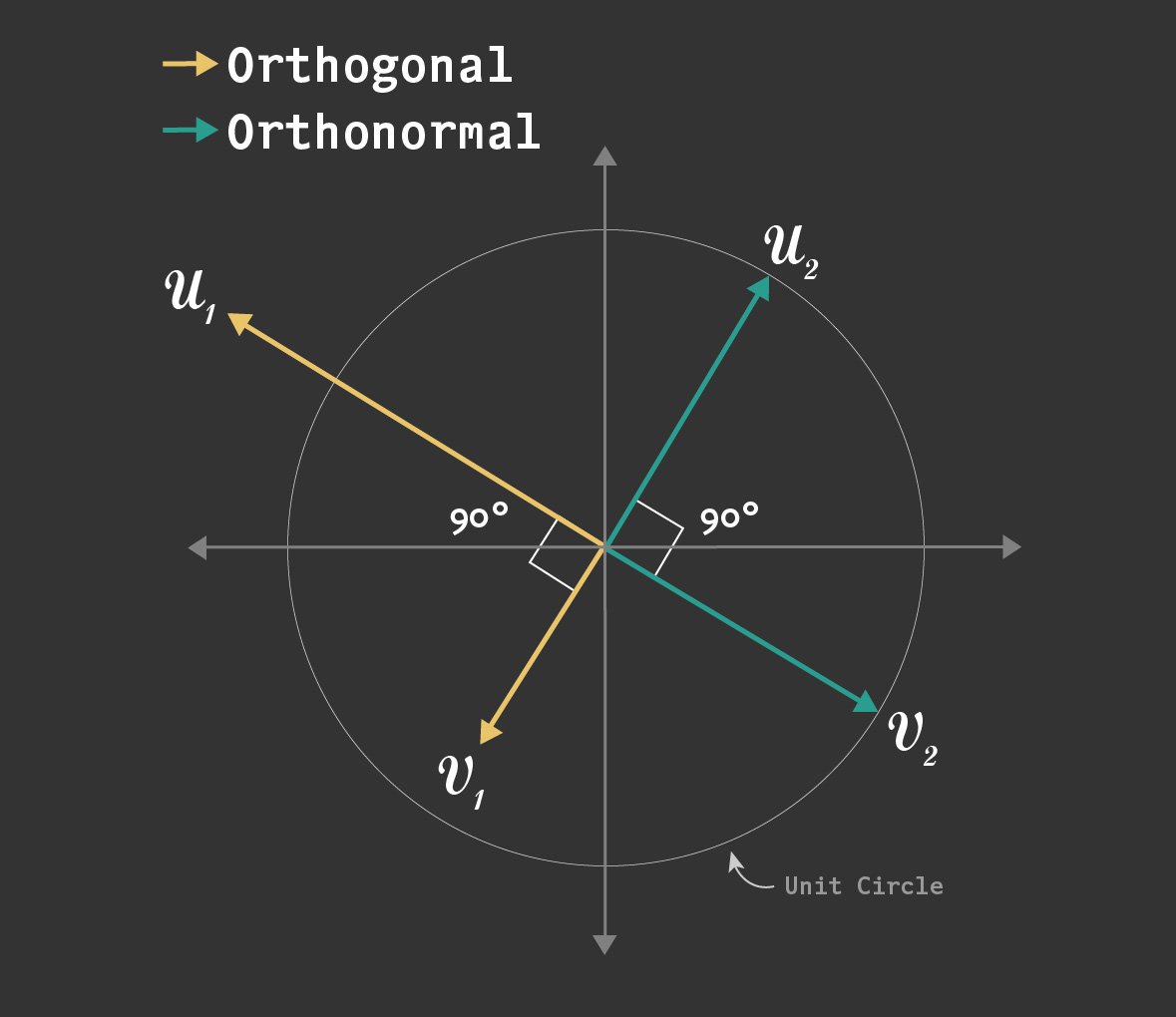
در فصل قبل با فضای هیلبرت آشنا شدیم. در این فصل، ابتدا مفهوم استقلال و وابستگی خطی را بررسی خواهیم کرد. سپس بعد و پایه