آموزش

در برخورد های کشسان، تمام انرژی قبل از برخورد پس از برخورد نیز در سامانه موجود است و چیزی تلف نمی شود؛ پس این برخورد

برخورد ناکشسان کامل (به معنی بهم چسبیدن) در صورتی اتفاق می افتد که جسمی با یک سرعت معین با جسمی ساکن برخورد کند و آن

در آموزش قبلی با پایستگی تکانه خطی آشنا شدیم؛ برخورد دو جسم در دو حالت انجام می شود، هرگاه در برخوردی انرژی جنبشی سامانه قبل

اگر یک سامانه منزوی باشد، به گونه ای که نیروی خارجی به آن وارد نشود؛ در این صورت تکانه خطی باید ثابت و پایسته بماند.

در آموزش های قبلی با مفاهیم تکانه و مرکز جرم و سامانه ذرات آشنا شدیم؛ می خواهیم تکانه کل یک سامانه ذرات را بررسی نماییم.

تعریف تکانه خطی یک ذره در فیزیک به شرح زیر است: که در آن p تکانه ذره، m جرم آن و v سرعت ذره می

در مقالات قبلی با مفهوم مرکز جرم آشنا شدیم؛ مکانی که تمامی ذرات یک سامانه را در آن متمرکز در نظر میگیریم و نیروهای وارد

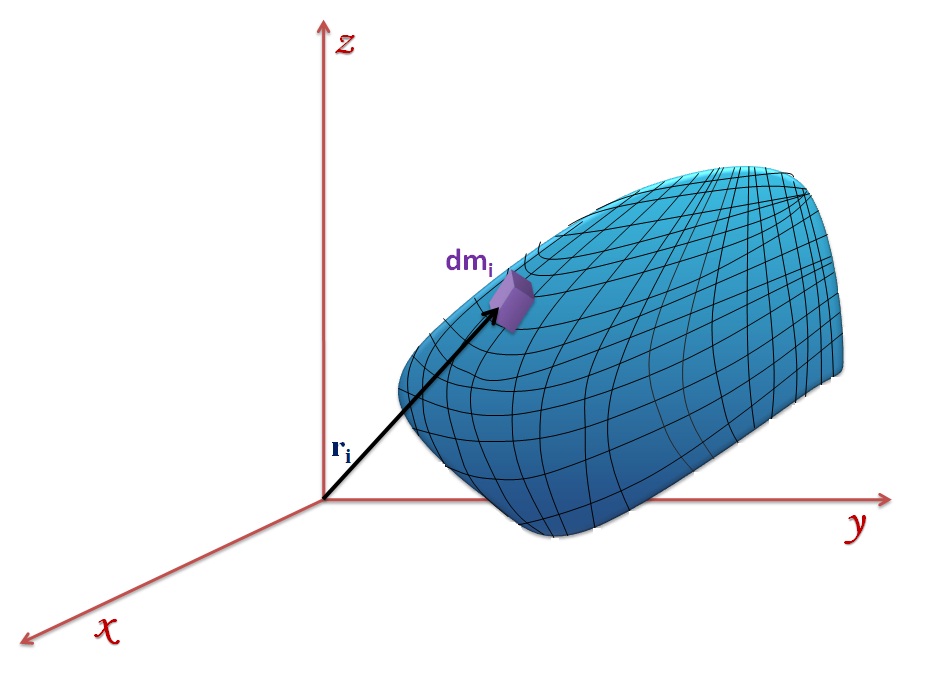
یک جسم شامل تعداد بسیار زیادی ذره (اتم) است و می توان آن را توزیعی پیوسته در نظر گرفت، پس فرم محاسبه مرکز جرم نیز

برای ساده سازی تحلیل حرکت و نیروهای وارده بر یک سامانه ذرات به آن ها نقطه ای به نام مرکز جرم نسبت می دهیم که