حد ؛ تعریف و قوانین

آموزش, آموزش ریاضی

اگر f تابعی از x باشد، در نقطه ای مانند c داریم (f(c. ممکن است در مواردی مقدار دقیق f در یک نقطه مانند c وجود نداشته باشد. در اینصورت تلاش میکنیم با کمترین فاصله ممکن به c نزدیک شویم تا مقدار حدودی (f(c را ( گرچه ممکن است وجود نداشته باشد ) بدست آوریم:

(1)

$\lim _{x\to c}f(x)=L$

تعبیر هندسی حد این است که روی محور x از دو طرف به c انقدر نزدیک می شویم تا به تصویر حدودی تابع روی محور y یعنی L برسیم.

تابع (f(x را در نظر بگیرید؛ اگر c در دامنه تابع f تعریف شده باشد و به توان از دو طرف، روی تابع به (f(c نزدیک شد؛ داریم:

(2)

$\lim_{x\rightarrow c}f(x)=f(c)$

*تمرین حل شده)

حد تابع $f(x)=x^{2}+1$ را در x→2 بدست آورید.

همانطور که می دانیم دامنه تابع برابر R است. پس طبق رابطه دوم حد تابع بدست می آید:

$\lim_{x\rightarrow 2}x^{2}+1=5$

قوانین حد

قوانین زیر بر عملیات های بین دو تابع در حد برقرار است:

*تمرین حل شده)

اگر دو تابع $\\ f(x)=x-1 \\ g(x)=x^2+1$ را داشته باشیم؛ حاصل حد f/g را در x→4 بدست آورید.

$\lim_{x\rightarrow 4}\frac{x-1}{x^2 +1}=\frac{3}{9}=\frac{1}{3}$

حد همیشه وجود دارد؟

پاسخ سوال خیر است؛ به نمودار تابع زیر دقت کنید:

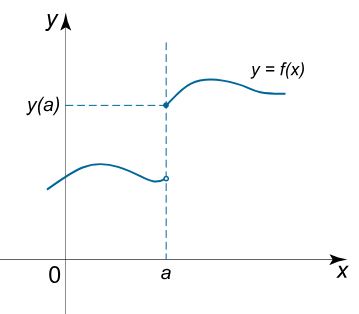
مقدار تابع در نقطه a برابر (y(a است، ما باید از دو طرف a را محاصره کنیم، زمانی که از طرف راست به آن نزدیک می شویم به (y(a نیز نزدیک می شویم اما زمانیکه از چپ به a نزدیکی پیدا می کنیم؛ به مقداری جز (y(a نزدیک شده ایم. پس نمی توان از دو طرف به a نزدیک شد و جوابی واحد پیدا کرد. در این صورت حدی در نقطه a وجود ندارد.

SCIENCIO

حد ؛ تعریف و قوانین

دیدگاهتان را بنویسید لغو پاسخ