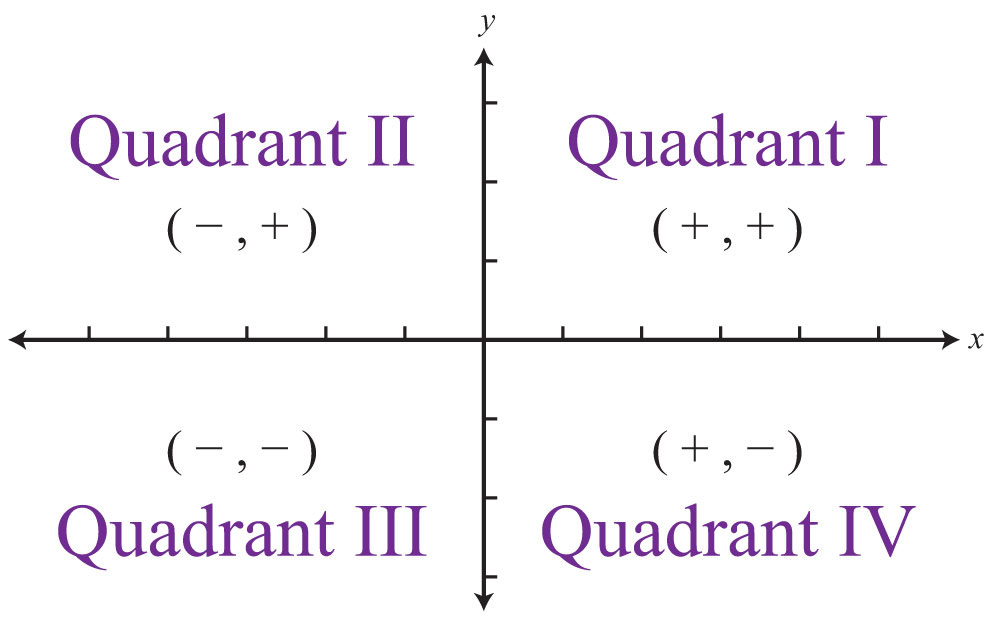
دستگاه مختصات دکارتی ( کارتزین )
در این مقاله به بررسی دستگاه مختصات دکارتی یا کارتزین خواهیم پرداخت؛ این دستگاه نام خود را از رنه دکارت ریاضی دان و فیلسوف فرانسوی

در این مقاله به بررسی دستگاه مختصات دکارتی یا کارتزین خواهیم پرداخت؛ این دستگاه نام خود را از رنه دکارت ریاضی دان و فیلسوف فرانسوی

در مقالات قبلی با انتگرال های مستقیم و همچنین روش کارآمد انتگرال جزء به جزء برای محاسبه برخی انتگرال های پیچیده کاربرد داشت؛ آشنا شدیم.

در مقالات قبلی با مقدمات انتگرال، انتگرال چند جمله ای توان دار و خواص انتگرال، انتگرال توابع مثلثاتی و همچنین روش کارآمد انتگرال گیری جزء

در این مقاله می خواهیم با ابزاری کارامد برای محاسبه برخی از انتگرال ها که محاسبه مستقیم آنها بعضا پیچیده و حتی غیرممکن باشد؛ آشنا

در دو مقاله قبلی با مقدمات و تعاریف انتگرال و همچنین انتگرال چند جمله ای توان دار و برخی خواص انتگرال آشنا شدیم. در این

در مقاله قبل با مقدمات و تعاریف انتگرال معین و نامعین آشنا شدیم؛ مشابه روندی که در مشتق چند جمله ای توانی مشاهده کردیم را

به سادگی می توان انتگرال معین را مساحت علامت دار میان یک تابع و محور x ها در بازه ای معین تعریف کرد. که نماد

در این مقاله قصد داریم با نحوه مشتق گیری از یک عبارت نمایی یا لگاریتمی آشنا شویم. مشتق تابع نمایی یکی از دلایل متعددی که

در مقالات قبلی با مفهوم تابع نمایی و لگاریتم آشنا شدیم؛ یکی از مهم ترین توابع نمایی، توابع نمایی بر پایه عدد نپر ( با

در مقاله پیشین با مفهوم و تعریف لگاریتم آشنا شدیم؛ هدف از این مقاله، آشنایی با اتحاد ها و روابط پرکاربردی است که میان لگاریتم