در این مقاله به بررسی دستگاه مختصات دکارتی یا کارتزین خواهیم پرداخت؛ این دستگاه نام خود را از رنه دکارت ریاضی دان و فیلسوف فرانسوی گرفته شده که اولین بار این نمایش نظام مند یک نقطه در صفحه، ابداع نمود. این نمایش نموداری تحول عظیمی را در علوم مختلف بوجود آورد و توانایی تحلیل انسان از رفتارهای طبیعی و ریاضی را ارتقا داد. شناخت این دستگاه در ابعاد مختلف دارای اهمیت است.

رنه دکارت (1596 میلادی – 1650 میلادی) ریاضی دان و فیلسوف شهیر فرانسوی
یک بعد
در یک بعد، محور اعداد حقیقی خطی است که اعداد را از کوچکتر به بزرگتر، از طرف چپ به طرف راست مرتب می کند:

بر روی محور اعداد می توان جایگاه تقریبی یک عدد گنگ را نیز مشخص کرد؛ به طوری که به وسیله خواص فیثاغورثی، مثلث قائم الزاویه ای رسم می کنیم که طول وترش عدد گنگ مدنظر ما باشد. حال پرگار را از نقطه مدنظر به شعاع عدد گنگ باز کرده و کمانی رسم می کنیم که محور اعداد را قطع کند. نقطه برخورد کمان و محور عدد گنگ مورد نظر ماست.
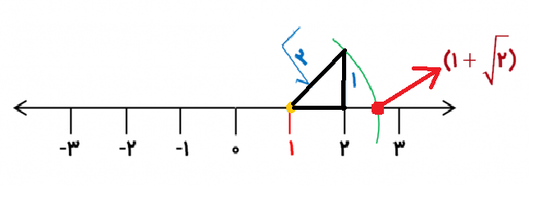
نمایش عدد گنگ 2√+1 روی محور اعداد، در اینجا نقطه یک شروع کار ماست و مثلث قائم الزاویه ای با دو ضلع قائمه به طول یک تشکیل می دهیم و با دستور بالا کمان را رسم می کنیم.
دو بعد
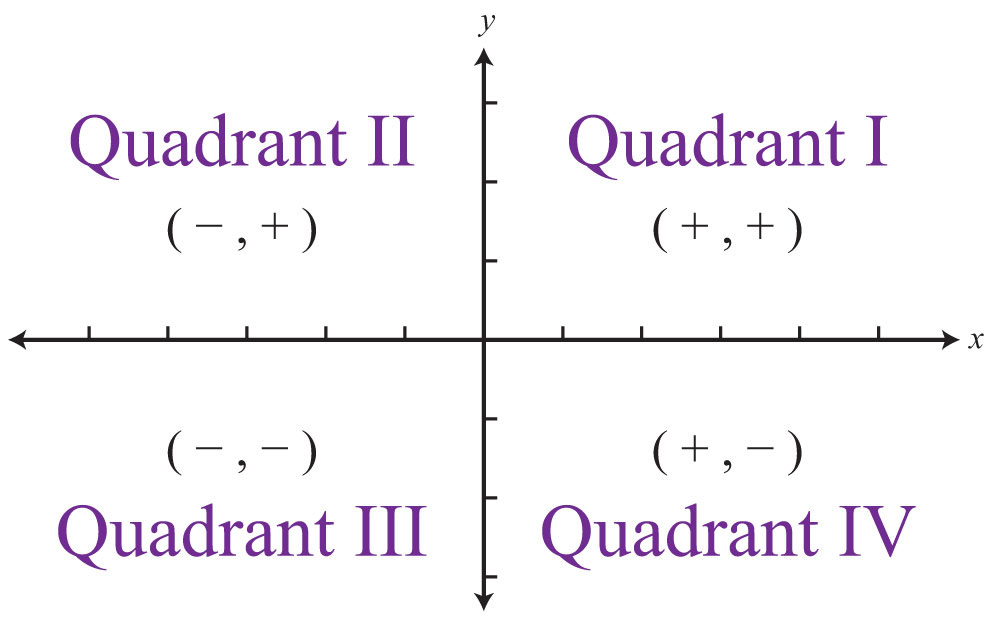
کارتزین دو بعدی که یک دستگاه مختصات بر روی صفحه است از دو محور اعداد تشکیل شده که برهم عمودند و محل برخورد دو محور مبدا مختصات نامیده می شود که در جایگاه 0 هر دو محور است. محور افقی را محور xها و محور عمودی را محور yها می نامند. شکل زیر نمایش چند نقطه روی دستگاه مختصات دکارتی است:
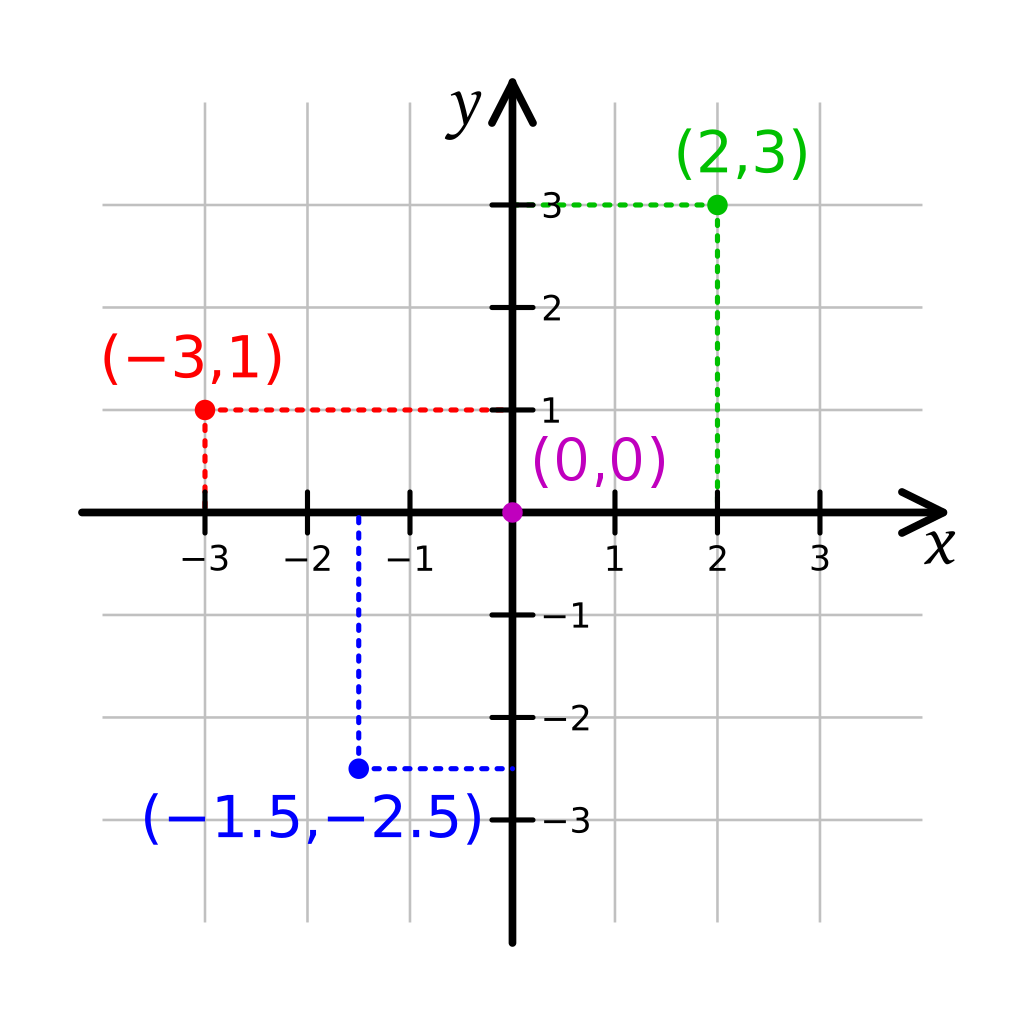
می توان مانند بالا نقاط را به صورت زوج مرتبی (x,y)=A و یا ماتریسی نمایش داد.
سه بعد
با توجه به اینکه درک ما از جهان پیرامون بصورت سه بعدی است؛ دستگاه مختصات سه بعدی اهمیت بالایی دارد. در مختصات دکارتی سه بعدی، سه محور عمود بر هم x,y,z وجود دارد که در مبدا مختصات با هم متقاطع اند. نمایش نقاط بر روی این دستگاه به صورت پرانتزی A=(x,y,z) یا ماتریسی قابل نمایش است. شکل زیر نمایشی از دستگاه مختصات سه بعدی و سه صفحه دو بعدی پایه آن یعنی (x=0,y=0,z=0) است:
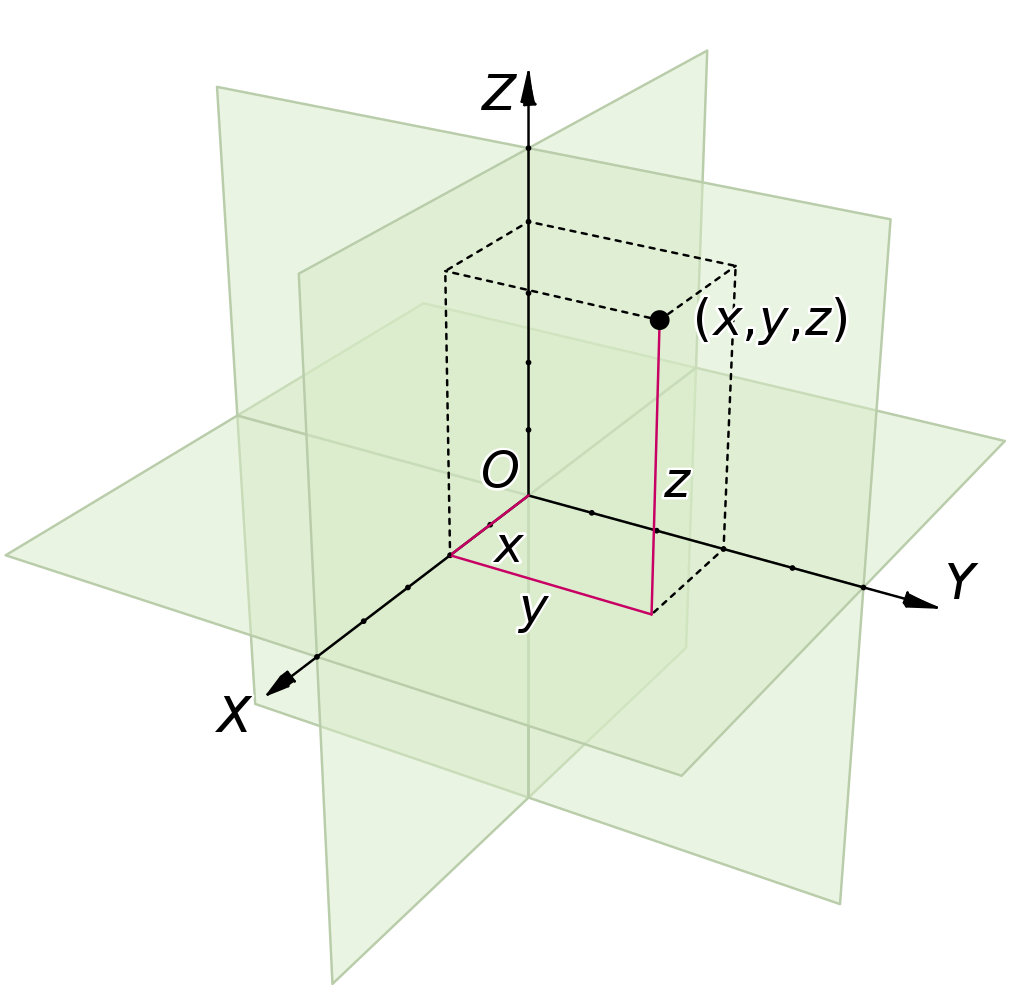
ابعاد بالاتر
بدلیل کاربردی بودن ابعاد بالاتر در علوم مختلف ( برای مثال تعریف کمیت ها و متغیرهای مختلف در یک سیستم مورد بررسی ) ؛ می توان دستگاه مختصات کارتزین را با هر تعداد بعد تعریف نمود.