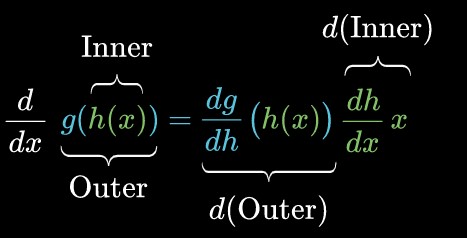
44 مشتق : قاعده زنجیره ای
در این فصل، قصد آشنایی با مشتق ترکیب توابع را داریم. ابتدا به این موضوع خواهیم پرداخت که توابع چگونه در یکدیگر ترکیب می شوند
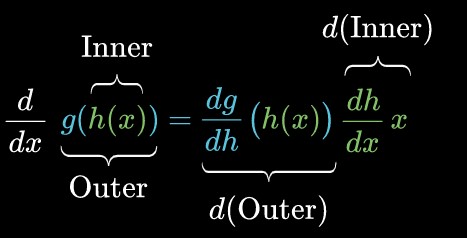
در این فصل، قصد آشنایی با مشتق ترکیب توابع را داریم. ابتدا به این موضوع خواهیم پرداخت که توابع چگونه در یکدیگر ترکیب می شوند
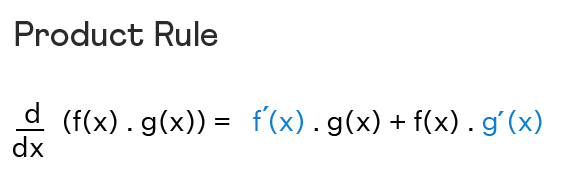
در این فصل به مشتق گیری از دو تابع که در یکدیگر ضرب شده اند؛ می پردازیم. به عنوان مثال، مشتق ضرب یک تابع مثلثاتی
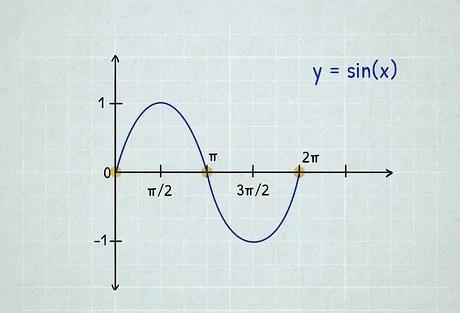
در این فصل به نحوه مشتق گیری از توابع مثلثاتی سینوس و کسینوس می پردازیم. باید در نظر داشت که بسیاری از رفتارهای سامانه های
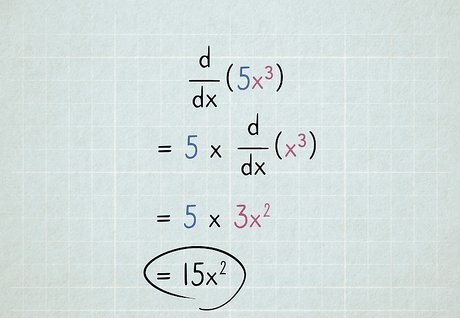
در این فصل از چندجمله ای های توانی مشتق می گیریم. فصل قبل با تعریف مشتق آشنا شدیم و در اینجا از همان تعریف برای
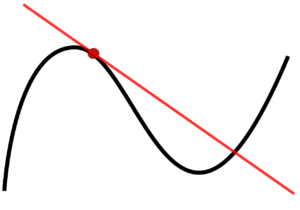
مفهوم مشتق، از مسئله تاریخی یافتن خط مماس بر منحنی در نقطه ای خاص بر می گردد. این مسئله اولین بار توسط فرما طرح و
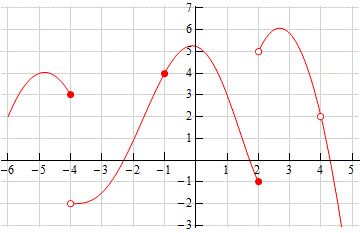
این فصل به پیوستگی اختصاص دارد. نام پیوستگی، محتوای آن را به خوبی توصیف می کند. زمانی که نمودار تابع ترکی برندارد یا ضربه ای

در این فصل به رفع ابهام در حد می پردازیم. گاهی ممکن است که حاصل هم صورت و هم مخرج کسر در حد صفر باشد.

در این فصل، به قضایای مهمی می پردازیم که محاسبه حد را در بسیاری از مسائل ساده تر می کند. البته می توان گفت که
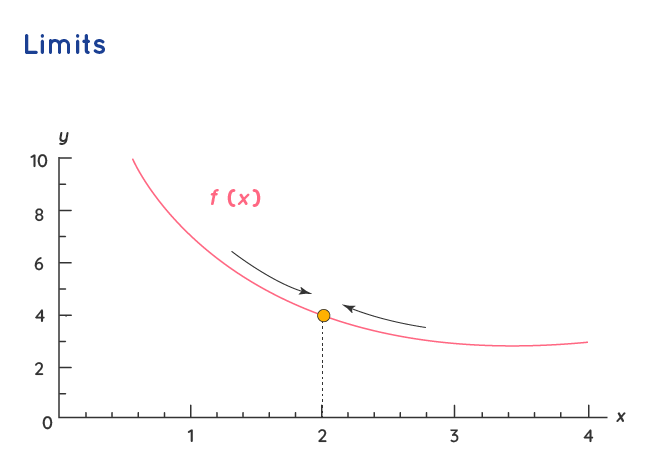
حد از مفاهیم بنیادی است که در یادگیری حسابان به آن نیازمندیم. حد معمولا در بررسی رفتار یک تابع، در نزدیکی نقطه ای خاص کاربرد
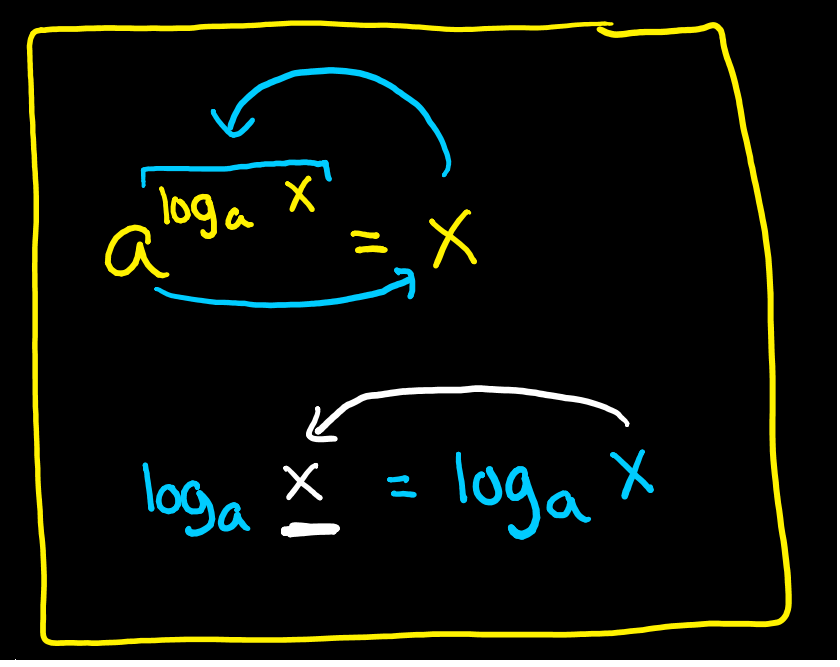
این فصل به ویژگی ها یا خواص لگاریتم اختصاص دارد که برای حل مسائل گوناگون مربوط به لگاریتم کارگشاست. ابتدا با برخی از خواص ساده
دانسته پروژه ای آموزشی است که در آن سعی شده مطالب به شکلی ساده و روان، در اختیار مخاطب قرار گیرد.
این اعداد شماره هر فصل دانسته است که برای سهولت در دسترسی و استناد به روابط، اشکال و تصاویر هرفصل مربوطه ایجاد شده.
بله، از طریق صفحه تماس با ما می توانید با ما ارتباط برقرار کنید و شاید افتخار همکاری با شما نصیب ما شد:)
برای پیشنهاد، انتقاد و تصحیح ایرادات علمی می توانید در پایان فصل مربوطه برای ما دیدگاه بگذارید و ما را از نظرات سازنده و ارزشمند خود آگاه سازید.

هرگز دل من ز علم محروم نشد
کم ماند ز اسرار که معلوم نشد
هفتاد و دو سال فکر کردم شب و روز
معلومم شد که هیچ معلوم نشد
حکیم عمر خیام