مفهوم مشتق، از مسئله تاریخی یافتن خط مماس بر منحنی در نقطه ای خاص بر می گردد. این مسئله اولین بار توسط فرما طرح و بررسی شد و سال ها بعد، نیوتون و لایپ نیتس به بررسی خط مماس بر در یک نقطه منحنی پرداختند.

1-40 شیب خط گذرنده از دو نقطه منحنی

می دانیم رابطه شیب خطی که از دو نقطه خاص $A=(x_{a},y_{a})$ و $B=(x_{b},y_{b})$ می گذرد به صورت زیر است:

(1)

$\large m=\frac{y_{b}-y_{a}}{x_{b}-x_{a}}$

منحنی $y=f(x)$ را در نظر بگیرید؛ حال فرض کنید دو نقطه $A$ و $B$، بر روی منحنی $y=f(x)$ باشند. اکنون می توان مختصات دو نقطه را به صورت $A=(x_{a},f(x_{a}))$ و $B=(x_{b},f(x_{b}))$ بازنویسی کرد. مطابق رابطه (1)، شیب خط گذرنده از این دو نقطه از رابطه زیر بدست می آید:

(2)

$\large m=\frac{f(x_{b})-f(x_{a})}{x_{b}-x_{a}}$

*مثال 40-1)

معادله خط گذرنده از دو نقطه با طول $x=1$ و $x=5$ که بر روی منحنی $y=x^{2}$ واقع اند را بیابید.

پاسخ

شیب خط مدنظر سوال را از رابطه (2) بدست می آوریم:

$\large m=\frac{25-1}{5-1}=6$

از رابطه یک نقطه و شیب خط بهره می بریم:

$\large y-y_{0}=m(x-x_{0}) \rightarrow y-1=6(x-1) $

$\large \rightarrow y=6x-5$

2-40 خط مماس بر منحنی

برای رسم خط مماس بر منحنی می توان از ابتکاری جالب بهره برد. در بخش قبل خط گذرنده از دو نقطه را محاسبه کردیم. می توان این دو نقطه را آنقدر به یکدیگر نزدیک کرد تا شیب خط مماس بر منحنی را محاسبه کرد. حال می خواهیم خط مماس بر تابع $f(x)$ را در نقطه $x=a$ محاسبه کنیم. از حد بهره می بریم تا نقطه دوم را تا جایی که می شود به نقطه مدنظر نزدیک کنیم. شیب از رابطه ای همانند رابطه (2) بدست می آید؛ به شیب در هر نقطه تابع $f$، تابع مشتق می گوییم و آن را با نماد $f'(x)$ نشان می دهیم. تابع مشتق در $a$ از رابطه زیر محاسبه می شود:

(3)

$\large f'(a)=\displaystyle{\lim_{x\rightarrow a}{\frac{f(x)-f(a)}{x-a}}}$

می توان مشتق را به شکل دیگر و معادل رابطه بالا نیز تعریف کرد که در آن $h=x-a$ است:

(4)

$\large f'(a)=\displaystyle{\lim_{h\rightarrow 0}{\frac{f(a+h)-f(a)}{h}}}$

هرگاه حد (3) یا (4) موجود و متناهی باشد؛ تابع مشتق در آن نقطه خاص تعریف می شود.

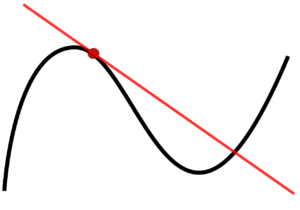
شکل 40-1، خط مماس بر منحنی در نقطه خاص

*مثال 40-2)

مشتق تابع $f(x)=x^{3}$ را در نقطه $x=2$ محاسبه کنید.

پاسخ

از رابطه (3) بهره می بریم تا مشتق یا شیب خط مماس در آن نقطه را محاسبه کنیم:

$\large \displaystyle{\lim_{x\rightarrow 2}{\frac{x^{3}-8}{x-2}}}$

صورت حد را تجزیه می کنیم:

$\large \displaystyle{\lim_{x\rightarrow 2}{\frac{(x-2)(x^{2}+2x+4)}{x-2}}}=\displaystyle{\lim_{x\rightarrow 2}{x^{2}+2x+4}}=12$

3-40 جمع بندی فصل

در این فصل با تعریف مشتق آشنا شدیم. مشتق کاربرد فراوانی در محاسبات ریاضی و دیگر علوم دارد. برای مثال سرعت لحظه ای یک متحرک، با مشتق گیری از منحنی مکان جسم بر حسب زمان آن مشخص می شود. همچنین بسیاری از مفاهیم پیشرفته تر در ریاضیات بوسیله مشتق پایه ریزی شده اند.

*1- با استفاده از ماشین حساب، عرض دو نقطه با طول $x=1$ و $x=2$ که بر روی منحنی $y=\sin(x)$ واقع اند را بیابید. سپس معادله خط گذرنده از این دو نقطه را بیابید.

*2- تابع $f'(x)$ را به ازای $f(x)=x^{2}$، محاسبه کنید. (راهنمایی: مشتق تابع را در نقطه $x=a$ بدست آورید)