حد از مفاهیم بنیادی است که در یادگیری حسابان به آن نیازمندیم. حد معمولا در بررسی رفتار یک تابع، در نزدیکی نقطه ای خاص کاربرد دارد. ممکن است که آن نقطه خاص، در خود تابع نیز وجود نداشته باشد اما بتوان رفتار تابع در نقاط نزدیک آن را مطالعه نمود.

1-36 تعریف

فرض کنید تابع $f$ در بازه ای حول $x=a$ (که $f(a)$ می تواند وجود داشته باشد یا نداشته باشد) تعریف شده باشد. زمانیکه با متغیر $x$ از دو طرف به $a$ نزدیک می شویم. تابع $f$ نیز همواره به مقداری حقیقی مثل $L$ نزدیک شود؛ آنگاه می گوییم حد تابع $f$ وقتی که $x$ به $a$ نزدیک می شود برابر $L$ است.

(1)

$\large \displaystyle{\lim_{x\rightarrow a}f(x)}=L$

برای مثال تابع $\frac{\sin x}{x}$ را در نظر بگیرید؛ تابع در $x=0$ تعریف نمی شود اما می توان در نزدیکی صفر تابع را محاسبه نمود؛ هرچقد x را چه از اعداد مثبت، چه از اعداد منفی به صفر نزدیک می کنیم؛ مقدار تابع نیز به یک نزدیک می شود. انگار که حول صفر تابع سینوس شبیه تابع همانی رفتار می کند. در این شرایط داریم:
(2)

$\large \displaystyle{\lim_{x\rightarrow 0}\frac{\sin x}{x}}=1$

به این نکته توجه کنید که لزوما حد تابع در یک نقطه با مقدار تابع در همان نقطه برابر نیست! شکل 35-1، به همین مسئله اشاره دارد.

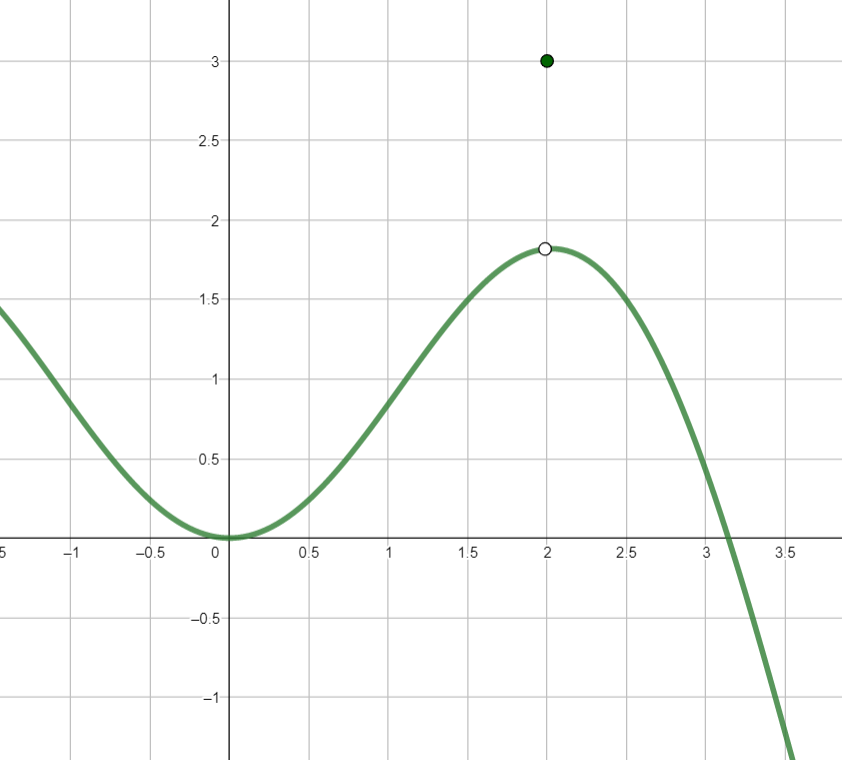
شکل 35-1، برای محاسبه حد تابع سبز رنگ، باید روی تابع حرکت کرد و عرض نقطه سفید رنگ را حد در $x=2$ نامید. درحالی که مقدار تابع در آن نقطه برابر با $y=3$ است.

*مثال 36-1)

با توجه به تابع دو ضابطه ای زیر، حد تابع در نزدیکی صفر را بیابید.

$\large \displaylines{f(x)=\left\{\begin{matrix}4x^{2} & x\neq 0\\ x+2 & x=0\end{matrix}\right.}$

پاسخ

در حد رفتار نزدیک نقطه مورد نظر دارای اهمیت است؛ پس حد تابع از ضابطه $x\neq0$ محاسبه می شود:

$\large \displaystyle{\lim_{x\rightarrow 0}f(x)}=4(0^{2})=0$

2-36 حد یک‌طرفه

اگر فقط از طرف راست(از اعداد بزرگتر به سمت اعداد کوچکتر روی محور $x$) به یک نقطه خاص نزدیک شویم و مقدار تابع در نزدیکی $x=a$، همواره به عدد حقیقی $L_{1}$ نزدیکتر می شد؛ آنگاه حد راست تابع در نقطه $x=a$ بدست آمده. حد راست را با توان مثبت برای $a$ نشان می دهیم:

(3)

$\large \displaystyle{\lim_{x\rightarrow a^{+}}f(x)}=L_{1}$

اگر فقط از طرف چپ(از اعداد کوچکتر به سمت اعداد بزرگتر روی محور $x$) به یک نقطه خاص نزدیک شویم و مقدار تابع در نزدیکی $x=a$، همواره به عدد حقیقی $L_{2}$ نزدیکتر می شد؛ آنگاه حد چپ تابع در نقطه $x=a$ بدست آمده. حد راست را با توان منفی برای $a$ نشان می دهیم:

(4)

$\large \displaystyle{\lim_{x\rightarrow a^{-}}f(x)}=L_{2}$

حد تابع در نقطه ای خاص در صورتی موجود است که حد چپ و راست در آن نقطه موجود و برابر باشند. بنابراین در صورتی که حد چپ و راست باهم تفاوتی داشته باشند؛ تابع در آن نقطه حد ندارد.

*مثال 36-2)

حد چپ و راست تابع در $x=0$ را بیابید و مشخص کنید که تابع در این نقطه حد دارد یا خیر.

$\large \displaylines{g(x)=\left\{\begin{matrix}\cos(x) & x< 0\\ x & x\geq 0\end{matrix}\right.}$

پاسخ

برای حد راست از ضابطه پایینی و برای حد چپ از ضابطه بالایی استفاده می کنم:

$\large \displaystyle{\lim_{x\rightarrow 0^{-}}g(x)}=\cos(0)=1$

$\large \displaystyle{\lim_{x\rightarrow 0^{+}}g(x)}=0$

$\large \displaystyle{\lim_{x\rightarrow 0^{-}}g(x)}\neq\large \displaystyle{\lim_{x\rightarrow 0^{+}}g(x)}$

تابع در $x=0$ حد ندارد.

3-36 جمع بندی فصل

در این فصل با مقدمات حد و حدهای یکطرفه که نقش مهمی در تعیین وجود حد دارند آشنا شدیم. همانطور که در ابتدا اشاره کردم؛ حد نقش مهمی در شناخت مشتق، انتگرال و بسیاری از مباحث ریاضیات و فیزیک بازی می کند.

*1- تعیین کنید که آیا در نقطه $x=0$ حد برای تابع علامت وجود دارد یا خیر؛ ضابطه زیر نشان دهنده تابع علامت است:

(5)

$\large \displaylines{sgn(x)=\left\{\begin{matrix}-1 & x<0 \\0 & x=0 \\1 & x>1\end{matrix}\right.}$