
69 جابجاگر
در این فصل به جبر جابجاگر (Commutator Algebra) می پردازیم. 1-69 تعریف جابجاگر دو عملگر $\hat{A}$ و $\hat{B}$ با $[\hat{A},\hat{B}]$ نمایش داده می شود. جابجاگر به

در این فصل به جبر جابجاگر (Commutator Algebra) می پردازیم. 1-69 تعریف جابجاگر دو عملگر $\hat{A}$ و $\hat{B}$ با $[\hat{A},\hat{B}]$ نمایش داده می شود. جابجاگر به
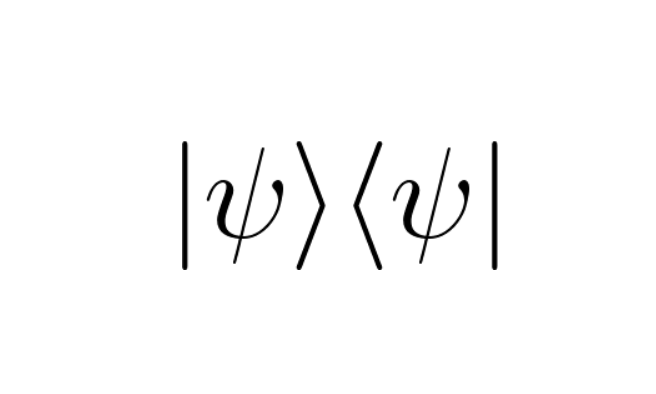
1-68 تعریف عملگر تصویر (projection operator)، عملگری هرمیتی است که با مجذور (مربع) خود برابر است. دو شرط زیر به طور کامل عملگر تصویر $\hat{P}$
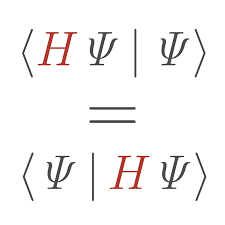
الحاقی هرمیتی یا مزدوج هرمیتی (Hermitian adjoint or conjugate) عملگر، موضوع بحث من در این فصل است. 1-67 تعریف الحاقی هرمیتی هر چیز را با
یکی از مفاهیم بنیادی در صورت بندی مکانیک کوانتومی، عملگر است. در این فصل با تعریف عملگر و چند عملگر خاص که در مکانیک کوانتوم

حالت فیزیکی یک سامانه کوانتومی، با عنصرهای فضای هیلبرت نمایش می دهیم. این عناصر، بردارهای حالت نامیده می شوند. بردارهای حالت در پایه های متفاوت

توابع انتگرال پذیر مجذوری و ضرب داخلی در فضای توابع، بحث این فصل است. در فضای توابع، بردارها با تابع مختلط و ضرب داخلی با
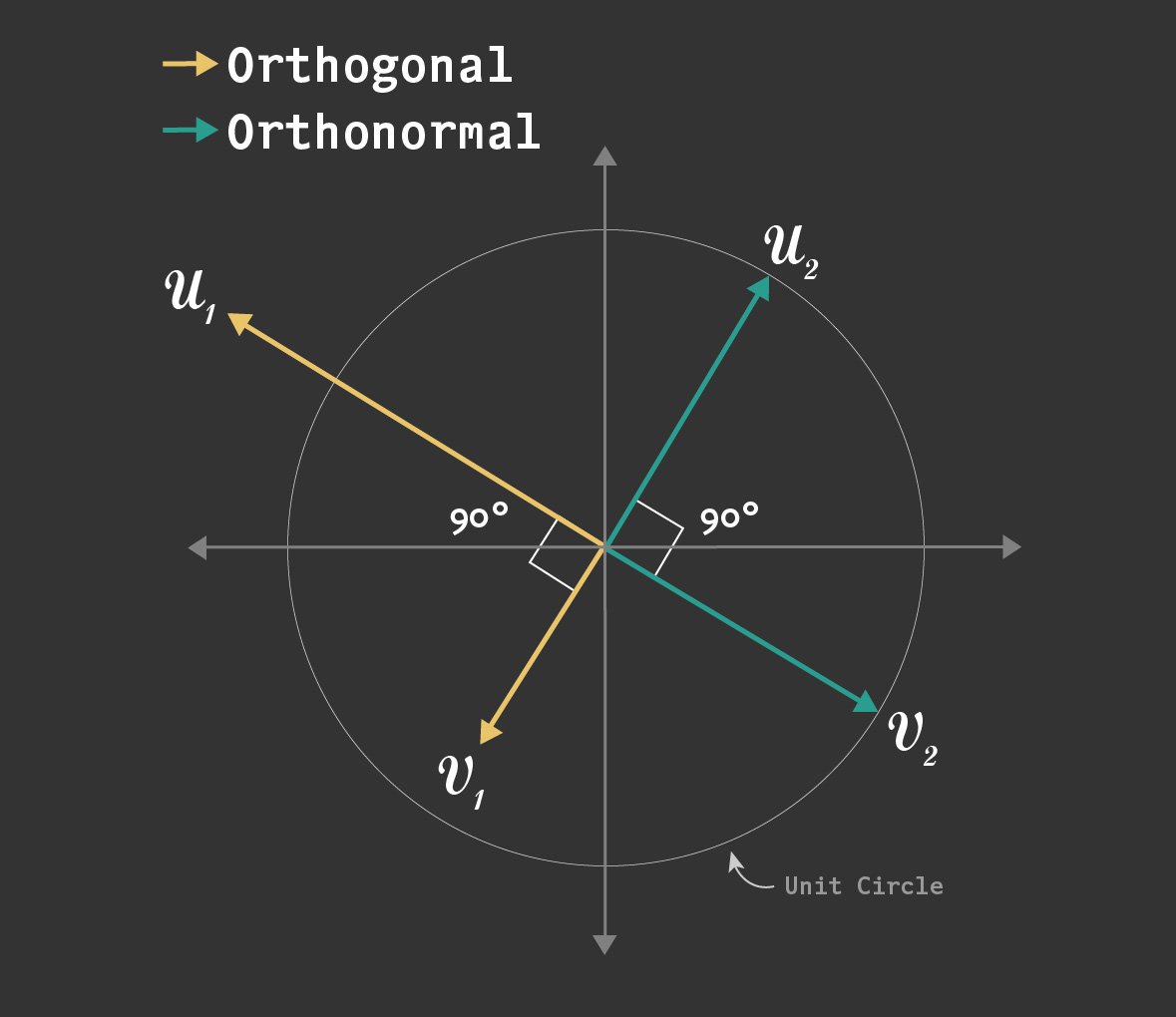
در فصل قبل با فضای هیلبرت آشنا شدیم. در این فصل، ابتدا مفهوم استقلال و وابستگی خطی را بررسی خواهیم کرد. سپس بعد و پایه
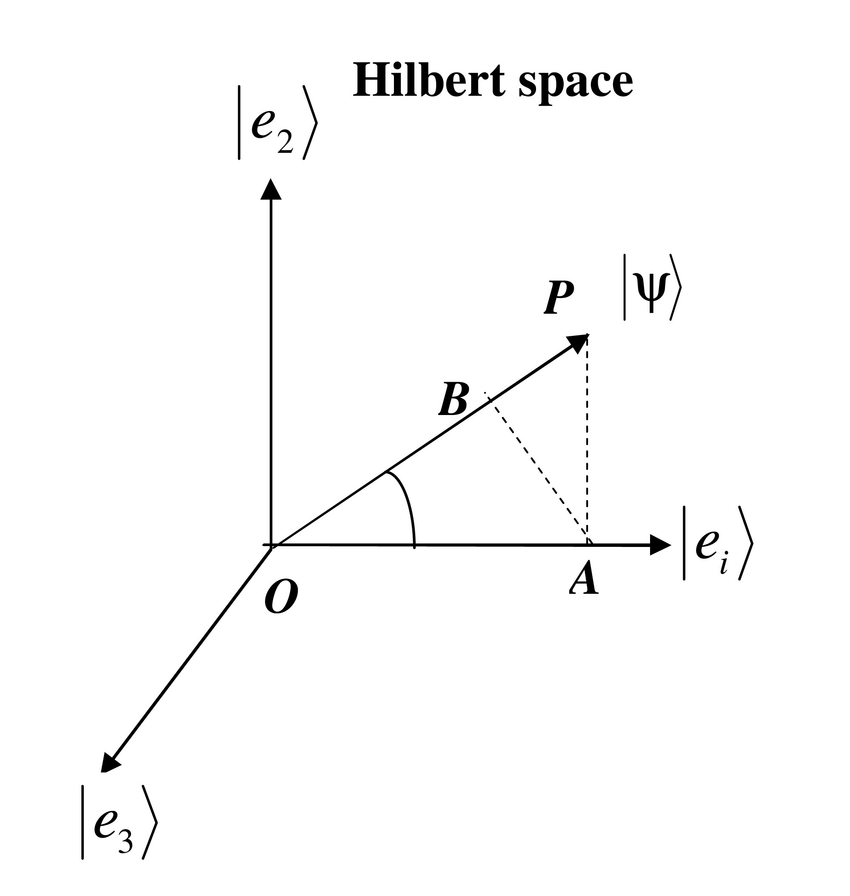
در سلسله فصل هایی به مفاهیم و مطالب مکانیک کوانتوم می پردازم. برای اینکه دستیابی به مطالب ساده تر باشد؛ فصل ها کوتاه ترند تا
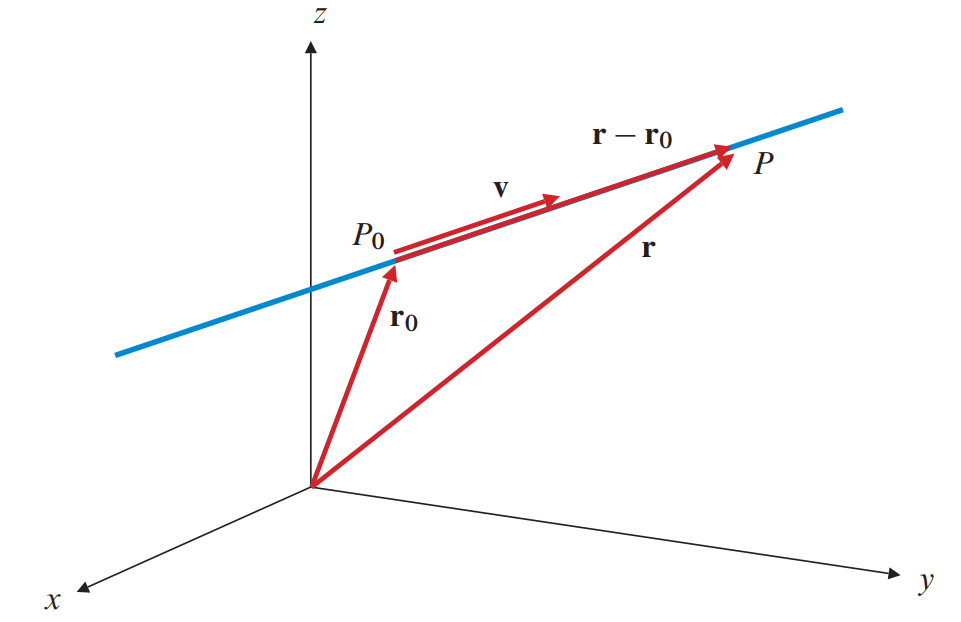
از کنار هم قرار گرفتن نقاط در فضای $\mathbb{R}^3$ ، خط تشکیل می شود. همانطور که در فصل قبل دیدیم؛ محل برخورد دو صفحه غیرموازی
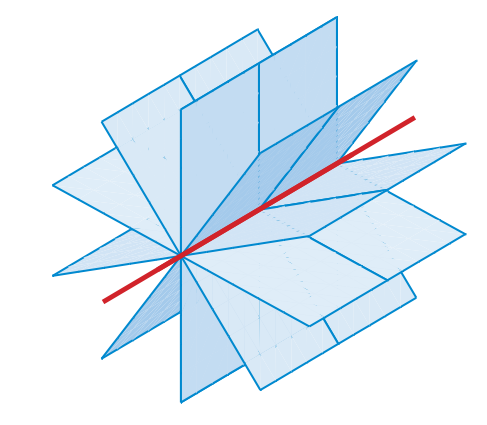
صفحه شکلی دوبعدی است که می خواهیم آن را در فضای سه بعدی بررسی کنیم و معادله صفحه را بدست آوریم. نقطه $P=(x,y,z)$ را در