در فصل 72 با عملگرهای یکانی آشنا شدیم. در این فصل، به چگونگی تبدیل اسکالرها، کت ها، براها و عملگرها تحت تبدیلات یکانی می پردازیم.

در فصول قبل عملگرها، حالت ها و ویژگی های آن ها را بررسی نمودیم. بحث این فصل درباره چگونگی یافتن ویژه مقدار ها (Eigenvalues) و

در این فصل به وارون یک عملگر کوانتومی و عملگرهای یکانی می پردازیم. 1-72 وارون یک عملگر در صورتی که عملگر وارون پذیر باشد (همانند

در این فصل به بررسی توابع عملگرهای کوانتومی می پردازیم. 1-71 تعریف فرض کنید که $F(\hat{A})$ تابعی از عملگر $\hat{A}$ باشد. در صورتی که $\hat{A}$

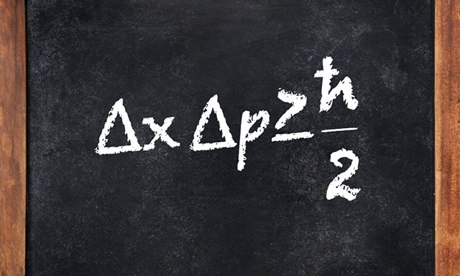
از کاربردهای جبر جابجاگر، محاسبه رابطه کلی برای حاصل ضرب عدم قطعیت های دو عملگر دلخواه است. رابطه ای که روابط عدم قطعیت هایزنبرگ را