
64 توابع انتگرال پذیر مجذوری
توابع انتگرال پذیر مجذوری و ضرب داخلی در فضای توابع، بحث این فصل است. در فضای توابع، بردارها با تابع مختلط و ضرب داخلی با

توابع انتگرال پذیر مجذوری و ضرب داخلی در فضای توابع، بحث این فصل است. در فضای توابع، بردارها با تابع مختلط و ضرب داخلی با
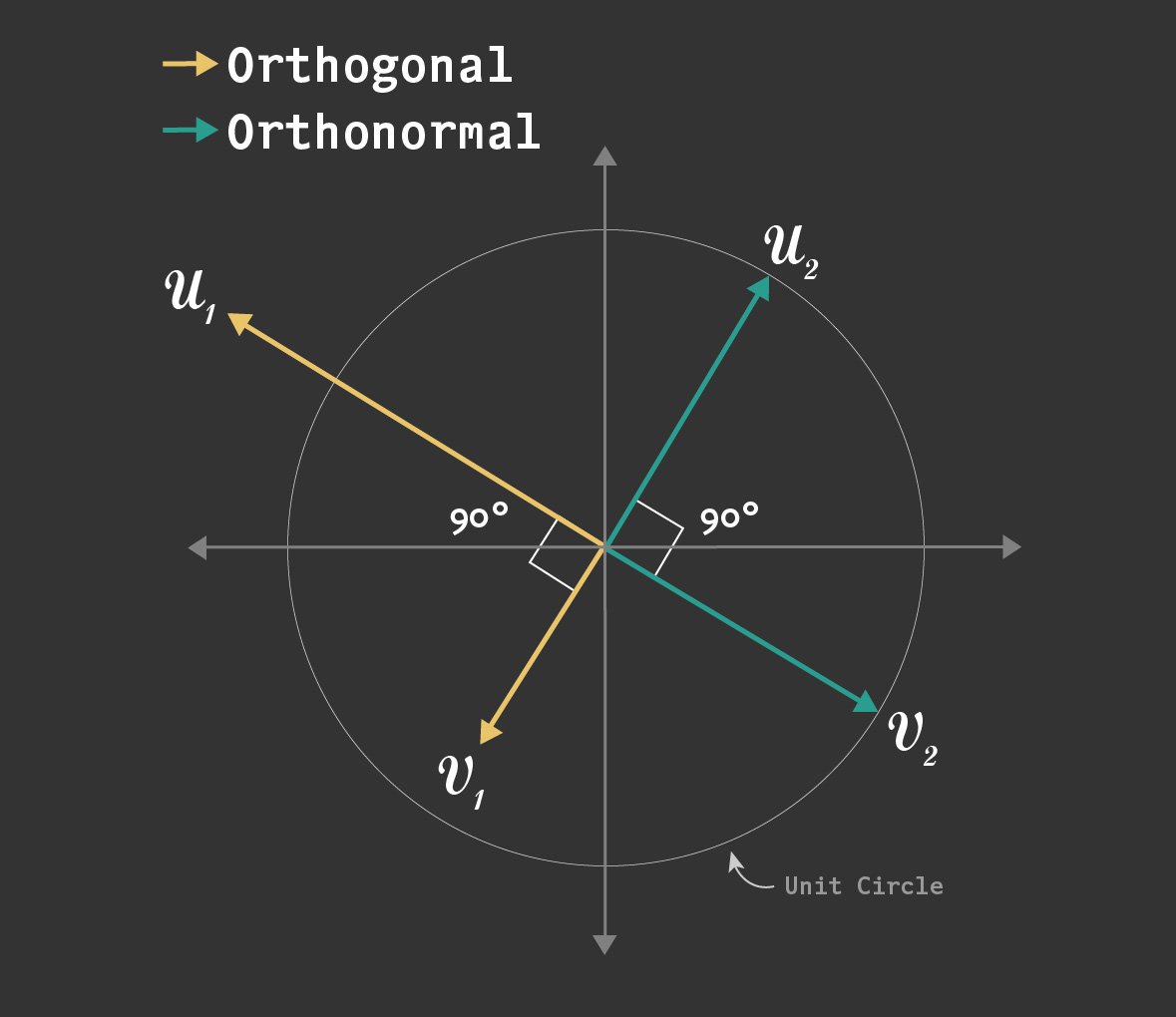
در فصل قبل با فضای هیلبرت آشنا شدیم. در این فصل، ابتدا مفهوم استقلال و وابستگی خطی را بررسی خواهیم کرد. سپس بعد و پایه
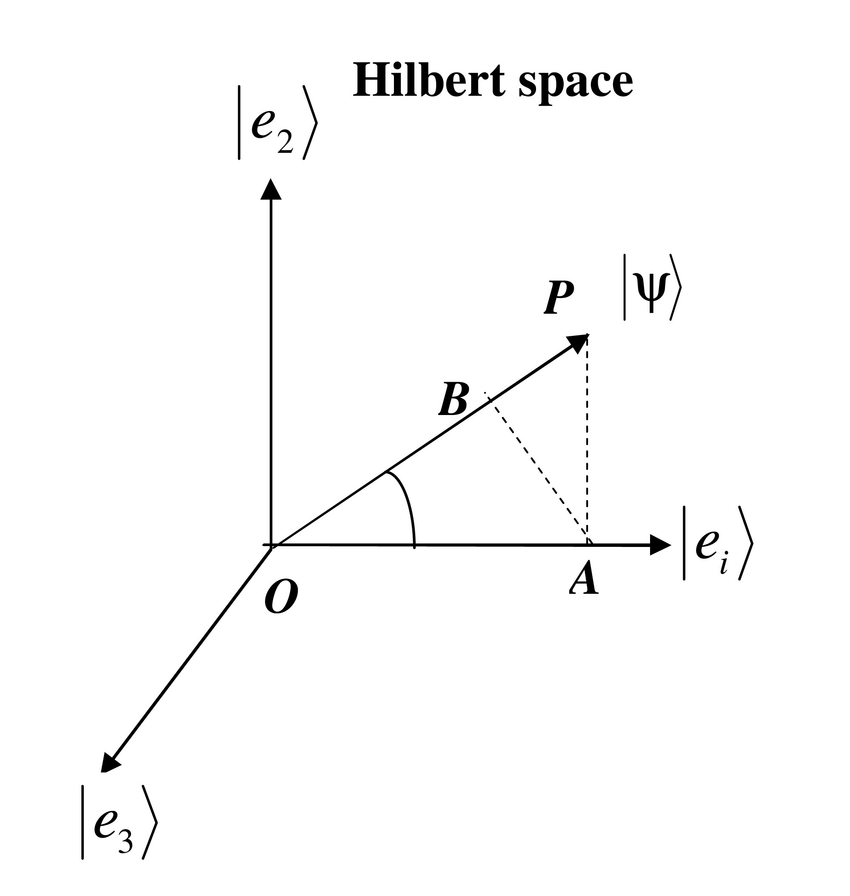
در سلسله فصل هایی به مفاهیم و مطالب مکانیک کوانتوم می پردازم. برای اینکه دستیابی به مطالب ساده تر باشد؛ فصل ها کوتاه ترند تا
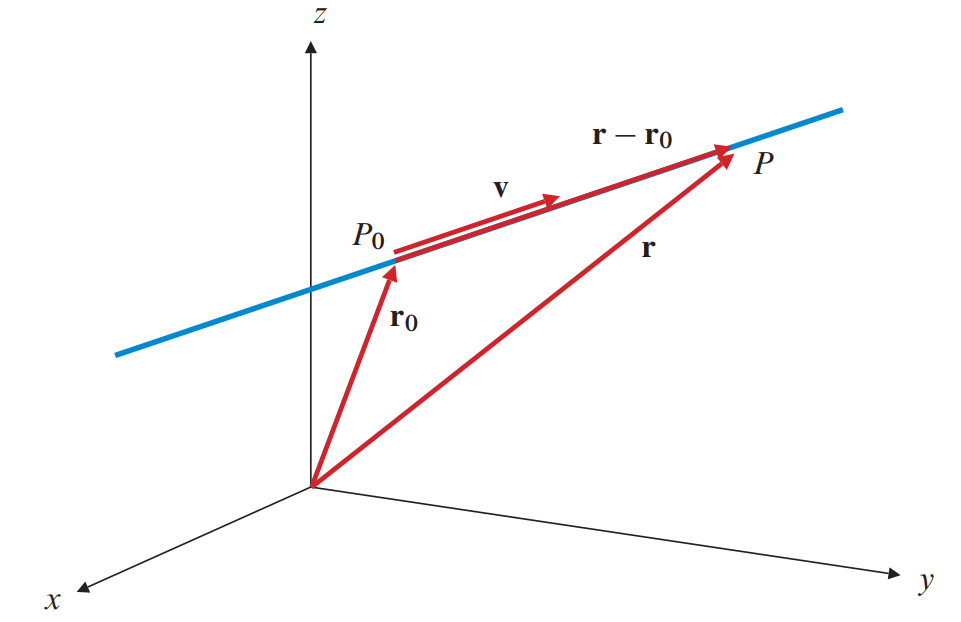
از کنار هم قرار گرفتن نقاط در فضای $\mathbb{R}^3$ ، خط تشکیل می شود. همانطور که در فصل قبل دیدیم؛ محل برخورد دو صفحه غیرموازی
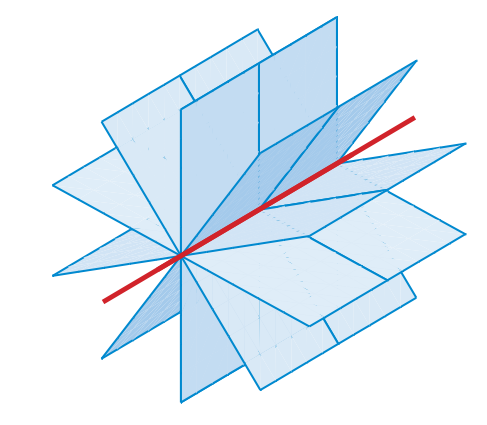
صفحه شکلی دوبعدی است که می خواهیم آن را در فضای سه بعدی بررسی کنیم و معادله صفحه را بدست آوریم. نقطه $P=(x,y,z)$ را در
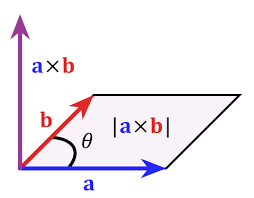
در فصل قبل با ضرب داخلی آشنا شدیم. ضرب خارجی عملی است که دو بردار سه مولفه ای را به عنوان ورودی می گیرد و یک
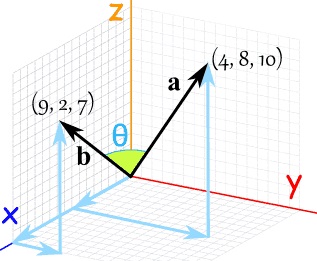
ضرب داخلی (ضرب نقطه ای یا ضرب اسکالر نیز گفته می شود)، عملی است که دو بردار را به عنوان ورودی می گیرد و یک
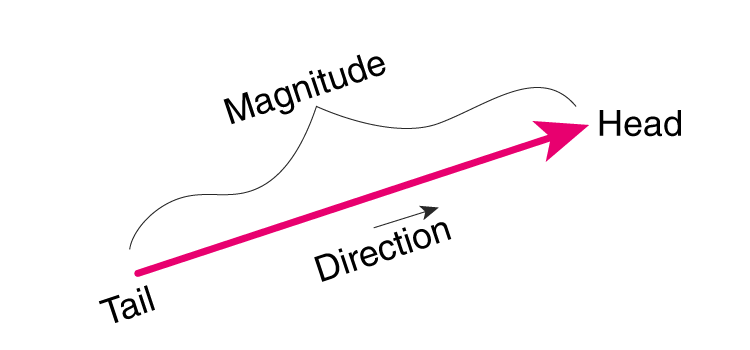
در علوم تجربی، گاها با کمیت هایی روبهرو می شویم که تنها دارای مقدار هستند. به این کمیت ها، کمیت اسکالر یا نرده ای می

ماتریس وارون (Inverse Matrix) مبحث این فصل است. همانند اعداد که در آن، معکوس (وارون) هرعدد ضربدر خود عدد، مساوی یک می شود $a\times a^{-1}=1$
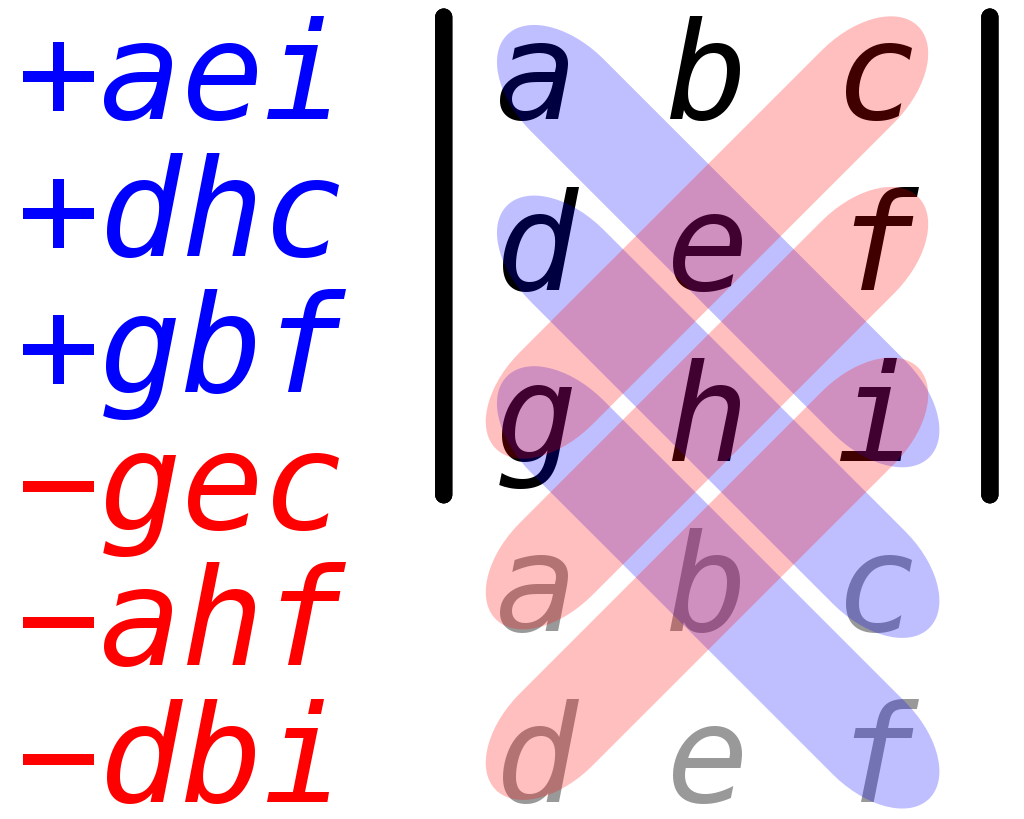
دترمینان (determinant) مفهومی کاربردی در محاسبات ماتریسی است. پس از آشنایی با ماتریس و عملیات های آن، خوب است که با دترمینان آشنا شویم. همانند
دانسته پروژه ای آموزشی است که در آن سعی شده مطالب به شکلی ساده و روان، در اختیار مخاطب قرار گیرد.
این اعداد شماره هر فصل دانسته است که برای سهولت در دسترسی و استناد به روابط، اشکال و تصاویر هرفصل مربوطه ایجاد شده.
بله، از طریق صفحه تماس با ما می توانید با ما ارتباط برقرار کنید و شاید افتخار همکاری با شما نصیب ما شد:)
برای پیشنهاد، انتقاد و تصحیح ایرادات علمی می توانید در پایان فصل مربوطه برای ما دیدگاه بگذارید و ما را از نظرات سازنده و ارزشمند خود آگاه سازید.

هرگز دل من ز علم محروم نشد
کم ماند ز اسرار که معلوم نشد
هفتاد و دو سال فکر کردم شب و روز
معلومم شد که هیچ معلوم نشد
حکیم عمر خیام