قانون دوم نیوتون در حرکت دورانی
در مقاله حرکت دورانی با شتاب ثابت، پی بردیم که شباهت های زیادی میان روابط دوران با شتاب ثابت و انتقال با شتاب ثابت وجود دارد؛ این تشابه در قانون دوم نیوتون نیز موجود است؛ اگر شتاب را با شتاب زاویه ای و جرم را با همانند دورانی اش، لختی دورانی جایگزین کنیم؛ از حاصل […]
گشتاور نیرو
همانطور که از دینامیک می دانیم؛ وارد کردن نیرو به جسمی ساکن می تواند سبب حرکت انتقالی جسم شود. در حرکت دورانی نیز عاملی مشابه با نیرو وجود دارد که سبب چرخش و دوران اجسام می شود که رابطه تنگاتنگی با نیرو دارد. این عامل گشتاور نامیده می شود. برای مثال فرد با وارد کردن […]
قضیه محورهای موازی
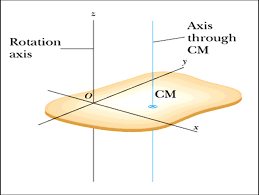
در مقاله قبلی با مفهوم انرژی جنبشی دورانی و لختی دورانی آشنا شدیم. با محاسبه انتگرال لختی دورانی همیشه می توان لختی دورانی حول محور مورد نظر را بدست آورد اما اگر این محور، موازی با محوری گذرنده از مرکز جرم جسم باشد؛ می توان با استفاده از رابطه زیر، لختی دورانی جسمی به جرم […]
انرژی جنبشی دورانی و لختی دورانی
در مقالات قبلی در مورد ویژگی های مختلف دوران صحبت کردیم؛ در این مقاله تصمیم داریم که به اجسام صلب در حال دوران حول یک محور ثابت، انرژی جنبشی نسبت دهیم. می دانیم که چرخش نیاز به انرژی جنبشی دارد. اما نمی توان از رابطه K=0.5mv2 استفاده نمود؛ زیرا این رابطه تنها انرژی جنبشی انتقالی […]
رابطه میان کمیت های خطی و زاویه ای
در مقالات قبلی با کمیت های دورانی و همچنین حرکت دورانی با شتاب زاویه ای ثابت آشنا شدیم. در تمامی روابط این مقاله مقیاس کمیت های دورانی، رادیان است. مکان اگر خط مرجع جسم، حول محور دوران با شعاع ثابت r به اندازه زاویه θ بچرخد؛ کمان ساخته شده، مسافت طی شده توسط جسم است: […]
حرکت دورانی با شتاب زاویه ای ثابت
در مقاله قبلی با کمیت های دورانی آشنا شدیم؛ خوشبختانه با توجه به نحوه تعریف این متغیرها، روابط دورانی با شتاب زاویه ای ثابت، بسیار شبیه به معادلات حرکت در خط راست با شتاب ثابت است که پیش از این مطالعه کرده ایم. یکی از راه های پی بردن به کمیت ها و روابط میان […]
دوران ؛ کمیت های دورانی
برای بررسی دوران یک جسم حول یک محور ثابت، محوری فرضی را به عنوان محور مرجع، عمود بر محور ثابت دوران در نظر می گیریم؛ مکان زاویه ای این خط که با جسم می چرخد؛ از رابطه زیر محاسبه می شود: (1) که در آن s طول کمان دایره و r شعاع دایره است. اگر […]
انتگرال ؛ تغییر متغیر
در مقالات قبلی با انتگرال های مستقیم و همچنین روش کارآمد انتگرال جزء به جزء برای محاسبه برخی انتگرال های پیچیده کاربرد داشت؛ آشنا شدیم. حال می خواهیم روشی را معرفی کنیم که بسیاری از انتگرال های پیچیده را با تغییر های متغیر مناسب، تبدیل به انتگرالی قابل محاسبه می کند. اگر تابع f(x) تابعی […]
انتگرال؛ انتگرال نمایی طبیعی، تابع اولیه یک ایکسم
در مقالات قبلی با مقدمات انتگرال، انتگرال چند جمله ای توان دار و خواص انتگرال، انتگرال توابع مثلثاتی و همچنین روش کارآمد انتگرال گیری جزء به جزء آشنا شدیم. در انتگرال گیری چند جمله ای پی بردیم که با فرمول عمومی این نوع انتگرال نمی توان از یک ایکسم یا ایکس به توان منفی یک […]
انتگرال ؛ انتگرال جزء به جزء
در این مقاله می خواهیم با ابزاری کارامد برای محاسبه برخی از انتگرال ها که محاسبه مستقیم آنها بعضا پیچیده و حتی غیرممکن باشد؛ آشنا شویم. از مشتق ضرب دو تابع می دانیم: حال از هر دو طرف تساوی انتگرال میگیریم: واضح است که حاصل ضرب دو تابع f و g برای مشتق خود یک […]