انرژی جنبشی دورانی و لختی دورانی

آموزش, آموزش فیزیک

در مقالات قبلی در مورد ویژگی های مختلف دوران صحبت کردیم؛ در این مقاله تصمیم داریم که به اجسام صلب در حال دوران حول یک محور ثابت، انرژی جنبشی نسبت دهیم. می دانیم که چرخش نیاز به انرژی جنبشی دارد. اما نمی توان از رابطه K=0.5mv² استفاده نمود؛ زیرا این رابطه تنها انرژی جنبشی انتقالی مرکز جرم جسم را بدست می دهد. پس باید هر جسم صلب را مجموعه ای را از ذرات با انرژی های جنبشی متفاوت در نظر گرفت که مجموع این ها می تواند انرژی جنبشی دورانی کل جسم را تامین کند:

$\\ K=\frac{1}{2}m_{1}v^{2}_{1}+\frac{1}{2}m_{2}v^{2}_{2}+... \\ \\ K=\sum \frac{1}{2}m_{i}v^{2}_{i}$

در اینجا می دانیم که سرعت برای تمامی ذرات یکسان نیست؛ اما می توان با استفاده از رابطه کمیت های خطی و زاویه ای، به کمیتی مانند سرعت زاویه ای رسید که برای تمامی ذرات با تقریب خوبی یکسان است(v=rω):

$\\ K=\sum \frac{1}{2}m_{i}v^{2}_{i}=K=\sum \frac{1}{2}m_{i}r_{i}^{2}\omega^{2}=\frac{1}{2}(\sum m_{i}r_{i}^{2})\omega^{2}$

کمیت جمع زده شده در رابطه بالا را لختی دورانی یا I می نامند که برای یک جسم صلب معین و یک محور دوران خاص و مشخص شده؛ مقداری ثابت است:

(1)

$K=\frac{1}{2}I\omega^{2}$

همینطور که در بالا لختی دورانی را تعریف کردیم؛ می توان آن را به جای سامانه ای از ذرات به یک جرم پیوسته نسبت داد که در آن بتوان به گونه ای روی جسم انتگرال گیری کرد که شامل هر دیفرانسیل (عنصر) جرم باشد:

(2)

$I=\int r^2 dm$

این انتگرال گیری معمولا کار ساده ای نیست اما در مراحل مقدماتی، می توان برای لختی دورانی هر جسم هندسی خاص به جدول مراجعه نمود:

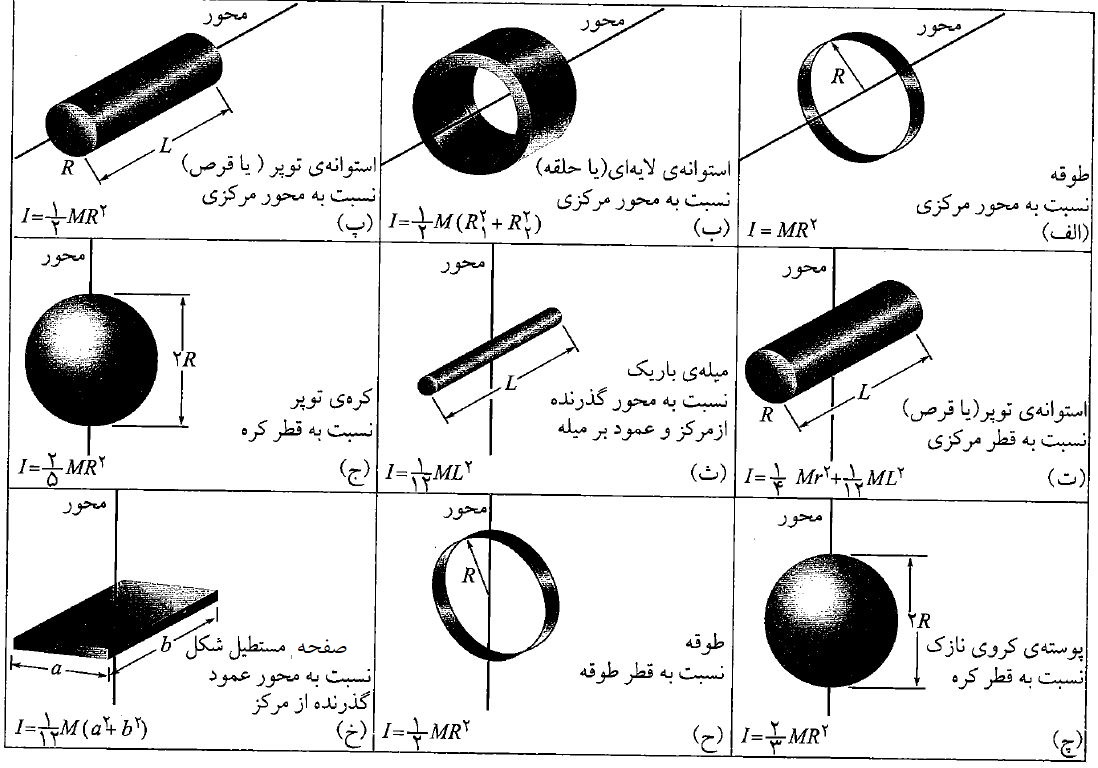
لختی دورانی برخی اجسام

*تمرین حل شده)

طوقه ای با شعاع 0.5 متر و جرم 0.5 کیلوگرم نسبت به قطر خود در با سرعت زاویه 2 رادیان بر ثانیه در حال دوران است؛ انرژی جنبشی دورانی طوقه را محاسبه نمایید.

از رابطه یک و جدول بالا استفاده می کنیم:

$K=\frac{1}{2}I\omega^2 =\frac{1}{2}(\frac{1}{2}MR^{2})\omega^2=\frac{1}{2}(\frac{1}{2}\times\frac{1}{2}\times \frac{1}{4})16=0.5\: J$

مسائل بیشتری می خواهید؟

بزودی

SCIENCIO

انرژی جنبشی دورانی و لختی دورانی

مسائل بیشتری می خواهید؟

درگاه انرژی جنبشی دورانی و لختی دورانی در کوئستیو

دیدگاهتان را بنویسید لغو پاسخ