رابطه میان کمیت های خطی و زاویه ای

آموزش, آموزش فیزیک

در مقالات قبلی با کمیت های دورانی و همچنین حرکت دورانی با شتاب زاویه ای ثابت آشنا شدیم. در تمامی روابط این مقاله مقیاس کمیت های دورانی، رادیان است.

مکان

اگر خط مرجع جسم، حول محور دوران با شعاع ثابت r به اندازه زاویه θ بچرخد؛ کمان ساخته شده، مسافت طی شده توسط جسم است:

(1)

$s=r\theta$

تندی

از معادله 1 بر حسب زمان مشتق میگیریم ( شعاع ثابت است ).

$\frac{ds}{dt}=r\frac{d\theta}{dt}$

سمت چپ معادله بزرگی سرعت خطی مماس بر مسیر حرکت یا تندی ظاهر شده و در سمت راست تندی زاویه ای مشاهده می شود:
(2)

$v=r\omega$

شتاب

مشابه روند بالا، با مشتق گیری از رابطه 2، رابطه ای میان شتاب خطی و شتاب زاویه پیدا می شود؛ اما در این حرکت دورانی، باتوجه به اینکه سرعت ظاهر شده، سرعت مماسی است. شتاب ظاهر شده در رابطه زیر نیز تنها شتاب مماسی جسم است و نه مجموع آن با شتاب مرکزگرای جسم:

(3)

$a_{t}=r\alpha$

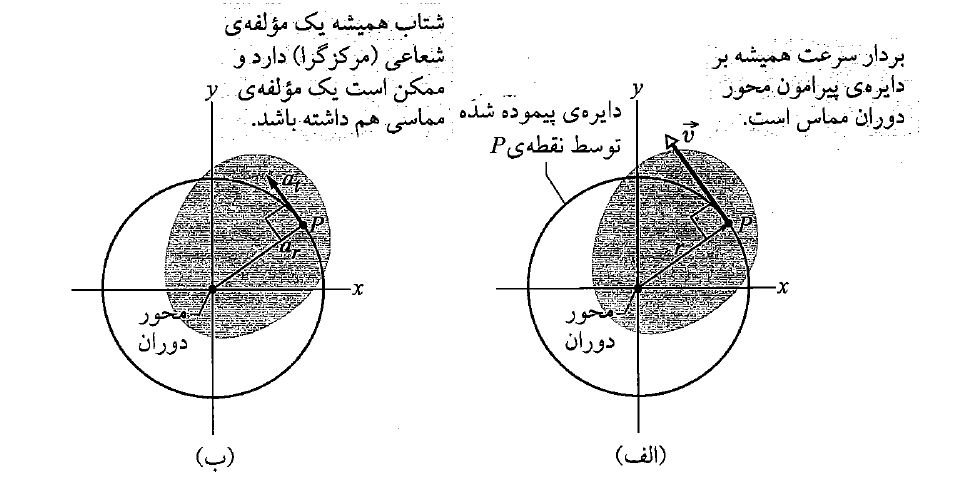
مولفه مماسی شتاب هم از قوانین حرکت دایره ای به سادگی بر حسب سرعت زاویه ای قابل محاسبه است:

(4)

$a_{r}=\frac{v^2}{r}= r\omega^2$

*تمرین حل شده)

در بازی قلعه: جنگ های صلیبی، یگانی تحت عنوان قلاب سنگ داران عرب در سربازخانه مسلمانان حضور داشت. فرض کنید یکی از این قلاب سنگ داران، قلاب سنگی را به مرکز مشت خود می چرخاند؛ رابطه زاویه با زمان به صورت $\theta=2t^{4}$ است. اگر شعاع چرخش 0.5m باشد؛ بزرگی سرعت خطی مماس بر مسیر در t=3s چقدر است؟

تندی زاویه ای را با مشتق گیری محاسبه می کنیم:

$\omega=8t^{3}\rightarrow v=r\omega \rightarrow v(t)=4t^{3}\rightarrow v(3)=108_{m/s}$

از سرعت بدست آمده مشخص است که محیط رخداد بازی بوده!

مسائل بیشتری می خواهید؟

بزودی

SCIENCIO

رابطه میان کمیت های خطی و زاویه ای

مکان

تندی

شتاب

مسائل بیشتری می خواهید؟

درگاه رابطه میان کمیت های خطی و زاویه ای در کوئستیو

دیدگاهتان را بنویسید لغو پاسخ