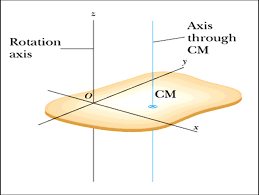
در مقاله قبلی با مفهوم انرژی جنبشی دورانی و لختی دورانی آشنا شدیم. با محاسبه انتگرال لختی دورانی همیشه می توان لختی دورانی حول محور مورد نظر را بدست آورد اما اگر این محور، موازی با محوری گذرنده از مرکز جرم جسم باشد؛ می توان با استفاده از رابطه زیر، لختی دورانی جسمی به جرم M، نسبت به محور مورد نظر ما را به لختی دورانی جسم نسبت به محور گذرنده از مرکز جرم ( ICOM ) و همچنین فاصله دو محور موازی از هم (h) مربوط کرد:
(1)
اثبات قضیه محورهای موازی
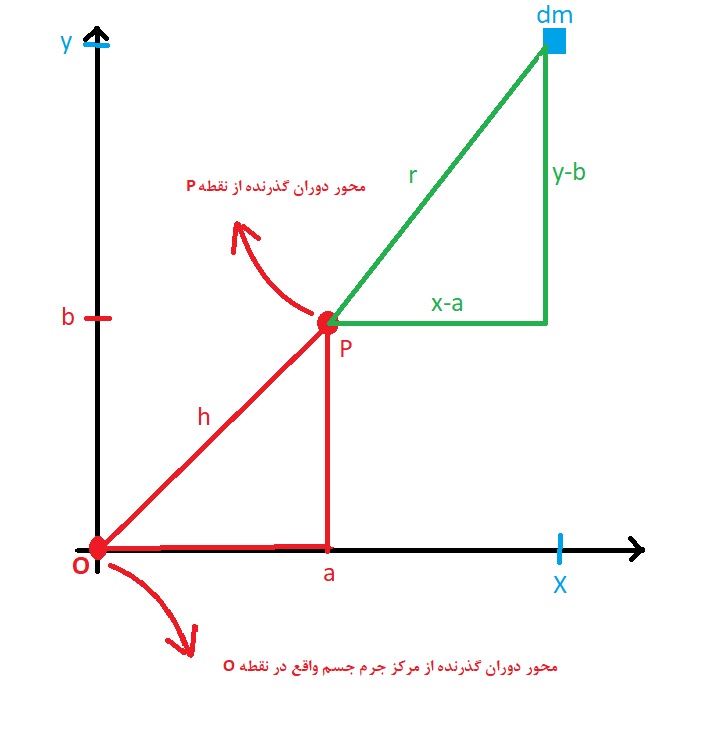
در شکل بالا نقطه O را مرکز جرم جسم در نظر میگیریم و آن را بر روی مبدا مختصات تنظیم می کنیم. دو محور موازی با هم و عمود بر صفحه شکل که از دو نقطه P و O می گذرند را در نظر می گیریم؛ می خواهیم با استفاده از عنصر دیفرانسیلی جرم جسم (dm) ، لختی دورانی جسم نسبت به محور گذرنده از نقطه P را محاسبه نماییم:
حال رابطه بالا را به شکل زیر باز می کنیم:
در سمت راست عبارت بالا جمله دوم و سوم صفر هستند؛ زیرا این دو انتگرال مختصات مرکز جرم را بدست می آورند که در اینجا مبدا مختصات در نظر گرفتیم؛ با توجه به قضیه فیثاغورث، جمله اول لختی دورانی نسبت به مرکز جرم و جمله چهارم انتگرال از عدد ثابت h2 است؛ پس رابطه یک اثبات می شود:
*تمرین حل شده)
لختی دورانی یک میله نازک با توزیع جرم یکنواخت، نسبت به محور گذرنده از مرکز جرم و عمود بر میله از رابطه قابل محاسبه است که در آن L طول میله است. لختی دورانی میله را نسبت به محور گذرنده از یک سر میله که موازی با محور فوق الذکر است را حساب کنید. (مرکز جرم میله دقیقا در وسط میله قرار دارد)
می دانیم که فاصله وسط میله از یک سر آن برابر با 0.5L است؛ پس به سادگی از قضیه محور های موازی داریم:

مسائل بیشتری می خواهید؟
بزودی