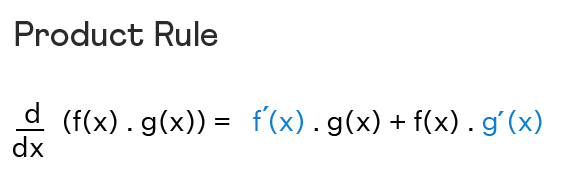
43 مشتق : قاعده ضرب
در این فصل به مشتق گیری از دو تابع که در یکدیگر ضرب شده اند؛ می پردازیم. به عنوان مثال، مشتق ضرب یک تابع مثلثاتی
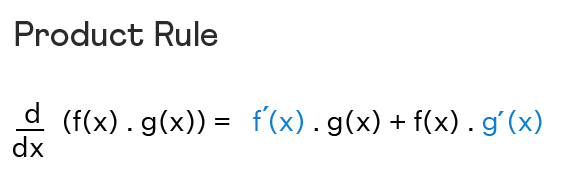
در این فصل به مشتق گیری از دو تابع که در یکدیگر ضرب شده اند؛ می پردازیم. به عنوان مثال، مشتق ضرب یک تابع مثلثاتی
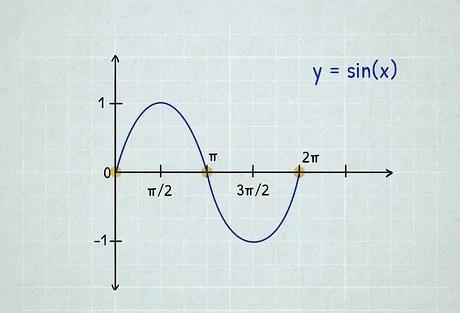
در این فصل به نحوه مشتق گیری از توابع مثلثاتی سینوس و کسینوس می پردازیم. باید در نظر داشت که بسیاری از رفتارهای سامانه های
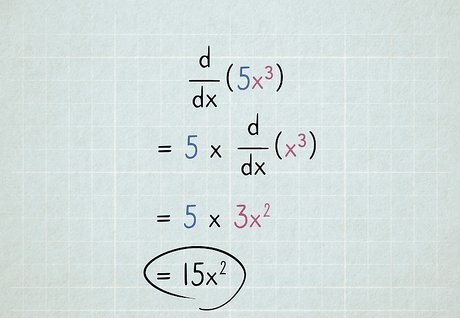
در این فصل از چندجمله ای های توانی مشتق می گیریم. فصل قبل با تعریف مشتق آشنا شدیم و در اینجا از همان تعریف برای
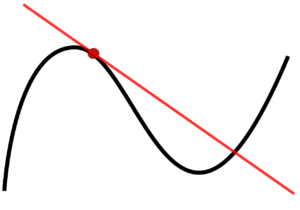
مفهوم مشتق، از مسئله تاریخی یافتن خط مماس بر منحنی در نقطه ای خاص بر می گردد. این مسئله اولین بار توسط فرما طرح و
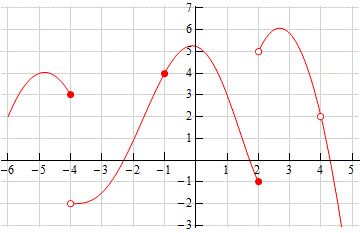
این فصل به پیوستگی اختصاص دارد. نام پیوستگی، محتوای آن را به خوبی توصیف می کند. زمانی که نمودار تابع ترکی برندارد یا ضربه ای

در این فصل به رفع ابهام در حد می پردازیم. گاهی ممکن است که حاصل هم صورت و هم مخرج کسر در حد صفر باشد.

در این فصل، به قضایای مهمی می پردازیم که محاسبه حد را در بسیاری از مسائل ساده تر می کند. البته می توان گفت که
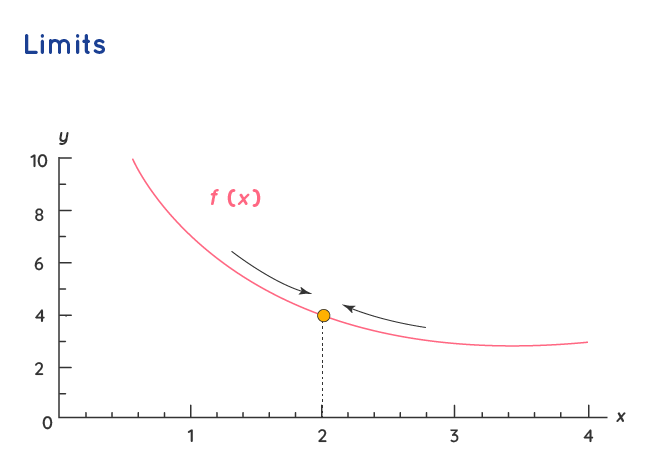
حد از مفاهیم بنیادی است که در یادگیری حسابان به آن نیازمندیم. حد معمولا در بررسی رفتار یک تابع، در نزدیکی نقطه ای خاص کاربرد
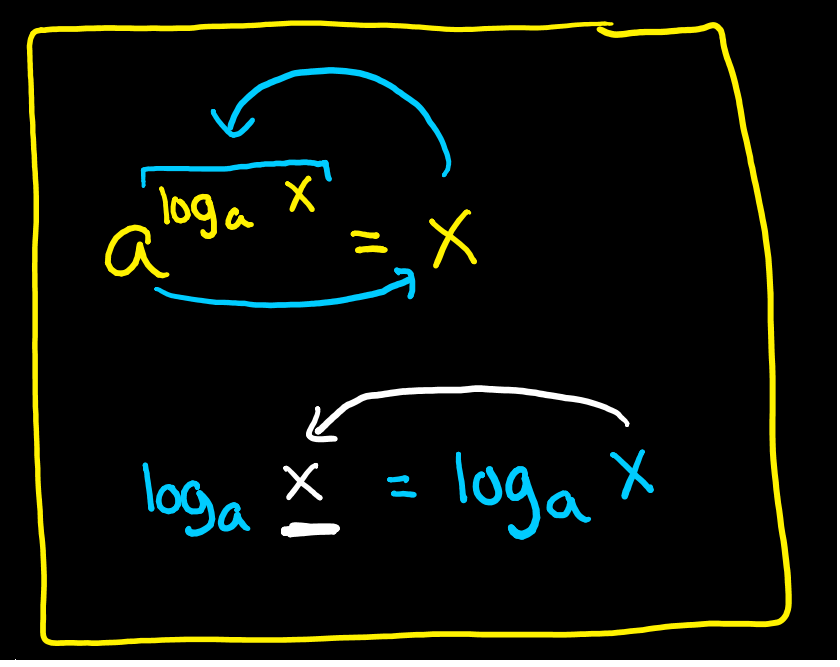
این فصل به ویژگی ها یا خواص لگاریتم اختصاص دارد که برای حل مسائل گوناگون مربوط به لگاریتم کارگشاست. ابتدا با برخی از خواص ساده
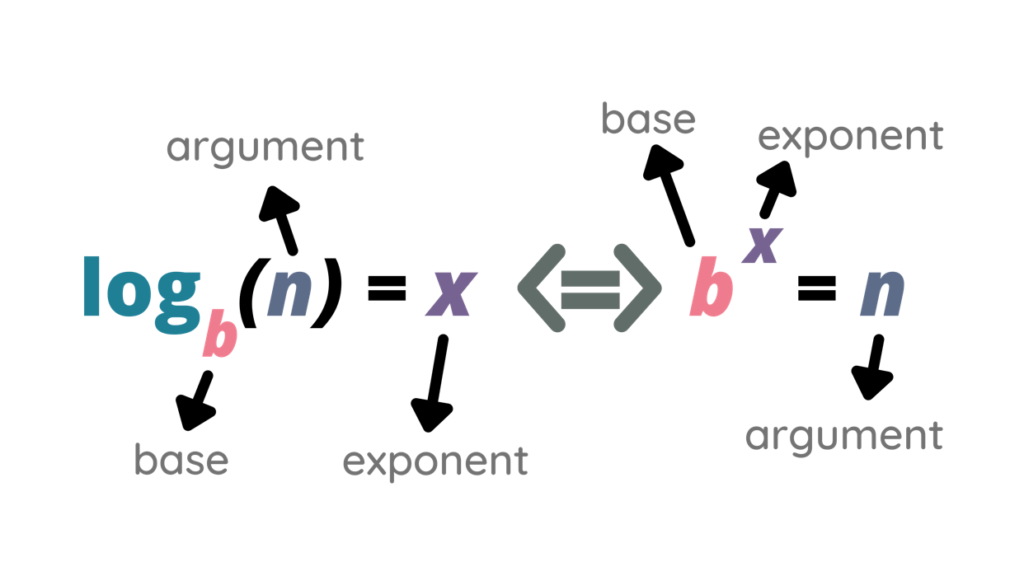
در فصل های گذشته با تابع وارون و تابع نمایی آشنا شدیم. تابع نمایی، تابعی یک به یک و وارون پذیر است. وارون تابع نمایی،