در فصل های گذشته با تابع وارون و تابع نمایی آشنا شدیم. تابع نمایی، تابعی یک به یک و وارون پذیر است. وارون تابع نمایی، را تابع لگاریتمی می نامیم. برای مثال تابع $y=2^{x}$ را باید طوری بنویسیم که $x=f(y)$ تا وارون تابع نمایی باشد. لگاریتم برای مدلسازی و تجزیه و تحلیل داده ها در تمامی علوم کاربرد دارد.
1-34 تعریف
عبارت نمایی با پایه $a$ که عددی مثبت و نامساوی با یک است را در نظر بگیرید:
(1)
$\large f(x)=a^{x}$
تابع وارون آن $f^{-1}$ به صورت لگاریتمی با پایه $a$ (مثبت و مخالف یک) تعریف می شود:
(2)
$\large f^{-1}(x)=\log_{a}x$
برای مثال، جدول زیر مختصات برخی از نقاط تابع نمایی $g(x)=2^{x}$ را نمایش می دهد:
| $\large g(x)=2^{x}$ | |
| $\large y$ | $\large x$ |
| 1 | 0 |
| 2 | 1 |
| 8 | 3 |
| 32 | 5 |
جدول 34-1، مقادیر تابع نمایی به پایه 2
وارون هر تابع، قرینه تابع به نسبت نیمساز ربع اول و سوم است. پس کافی است که جای مقدار $y$ و $x$ عوض شود تا مقادیر تابع لگاریتمی به پایه 2 بدست آید:
| $\large g^{-1}(x)=\log_{2}x$ | |
| $\large y$ | $\large x$ |
| 0 | 1 |
| 1 | 2 |
| 3 | 8 |
| 5 | 32 |
جدول 34-2، مقادیر تابع لگاریتمی به پایه 2
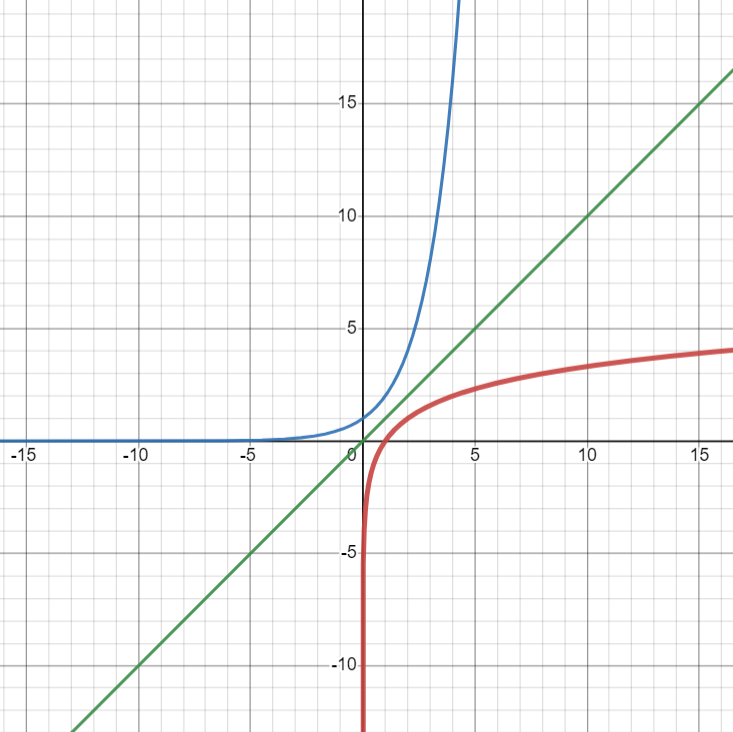
شکل 34-1، نمودارهای $y=\log_{2}x$ به رنگ قرمز، $y=x$ به رنگ سبز و $y=2^{x}$ به رنگ آبی
همانطور که از شکل 34-1 بنظر می رسد؛ دامنه تابع لگاریتمی همواره مثبت است (زیرا برد تابع نمایی همواره مثبت است و این دو وارون یکدیگرند) می توان از نظر رفتار، توابع لگاریتمی را به دو دسته تقسیم کرد که جلوتر به آن می پردازم.
2-34 توابع لگاریتمی با پایه بزرگتر از یک
تابع های لگاریتمی با پایه بزرگتر از یک، همانند $y=\log_{2}x$، با بزرگترشدن $x$، مقدار تابع افزایش می یابد. صفر در دامنه این تابع نیست اما مقدار تابع در کمی بزرگتر از صفر منفی بی نهایت است.
3-34 توابع لگاریتمی با پایه میان صفر و یک
توابع لگاریتمی با پایه میان صفر و یک، همانند $y=\log_{\frac{1}{2}}x$، با بزرگترشدن $x$، مقدار تابع کاهش می یابد. صفر در دامنه این تابع نیست اما مقدار تابع در کمی بزرگتر از صفر مثبت بی نهایت است.
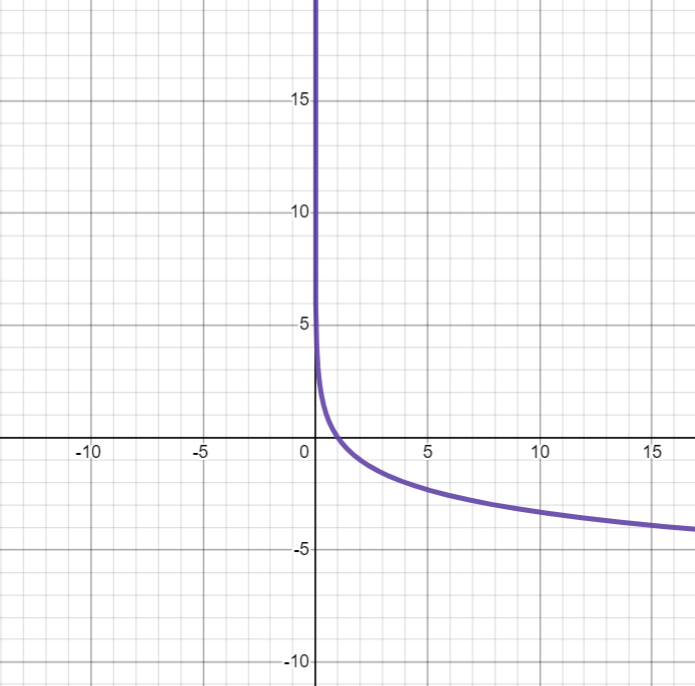
شکل 34-2، نمودار $y=\log_{\frac{1}{2}}x$
4-34 تابع لگاریتمی طبیعی
در فصل 33، عدد اویلر را معرفی کردم. اگر تابع لگاریتمی به پایه عدد اویلر باشد؛ تابع لگاریتمی طبیعی خوانده می شود و آن را با نماد $\ln(x)$ نمایش می دهیم:
(3)
$\large f(x)=\log_{e}x=ln(x)$
لگاریتم طبیعی تابع وارون نمایی طبیعی است.
5-34 جمع بندی فصل
با لگاریتم آشنا شدیم. در صورتی که پایه لگاریتم نوشته نشد $f(x)=\log x$، ممکن است به تابع لگاریتم طبیعی یا لگاریتم بر پایه 10 اشاره کند. متاسفانه در این مورد همه منابع هم نظر و یکدست نیستند. همانطور که در مقدمه گفتم؛ لگاریتم همانند نمایی، از دستاوردهای مهم بشر در زمینه علوم است. شیمی دان ها با استفاده از لگاریتم پی به میزان اسیدی بودن یا بازی بودن محلول شیمیایی می برند و فیزیکدان ها از آن برای مطالعه اصوات استفاده می کنند. برای رسم نمودارها از دسموس استفاده کردم.
| تمرینات فصل |
*1- معادله لگاریتمی زیر را حل کنید. (راهنمایی: برای پاسخ نهایی حتما به محدوده دامنه لگاریتم توجه کنید!)
$\large log_{7}(x^{2}-2)=log_{7}(x)$
ترتیب فصل |
قبلی |
فعلی |
بعدی |
عنوان |
33 تابع نمایی |
34 لگاریتم : مقدمه |
35 لگاریتم : ویژگی ها |




