در این فصل با توابع یک به یک و وارون تابع آشنا خواهیم شد. یک به یک بودن تابع به این معنی است که هر عضو برد تابع، دقیقا به یک عضو دامنه تابع مربوط باشد. به یاد داشته باشیم که هر تابعی لزوما یک به یک نیست.

1-32 توابع یک به یک

تابع زیر را در نظر بگیرید:

$\large f=\{(1,3),(2,4),(0,3)\}$

در تابع بالا، $3$ به دو عضو دامنه $f$ مربوط می شود. طبق تعریف، تابع بالا یک به یک نیست. حال تابع $g$ را در نظر بگیرید:

$\large g=\{(-1,2),(1,4),(6,8)\}$

در تابع $g$، هر عضو برد تنها به یک عضو دامنه مربوط است. این همان تعریف یک به یکی تابع است. پس تابع $g$، تابعی یک به یک است.

* مثال 32-1)

یک به یک بودن تابع $f(x)=x$ و تابع $g(x)=x^{2}$ را بررسی نمایید.

پاسخ

برای پی بردن به یک به یکی تابع، رسم نمودار توابع بسیار کاربردی است. هرگاه که خطی موازی محور x، بیش از یک نقطه را بر روی تابع قطع کند؛ تابع یک به یک نیست. چون در ازای یک عضو برد، بیش از یک عضو دامنه مربوط داریم. اما اگر هر خط موازی محور x، نمودار تابع را در حداکثر در یک نقطه قطع کند؛ تابع یک به یک است:

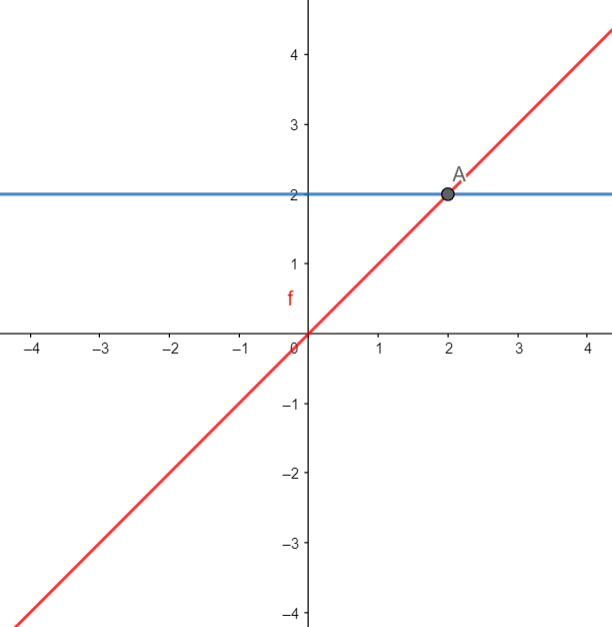
شکل 32-1، تابع $f(x)=x$ یک به یک است.

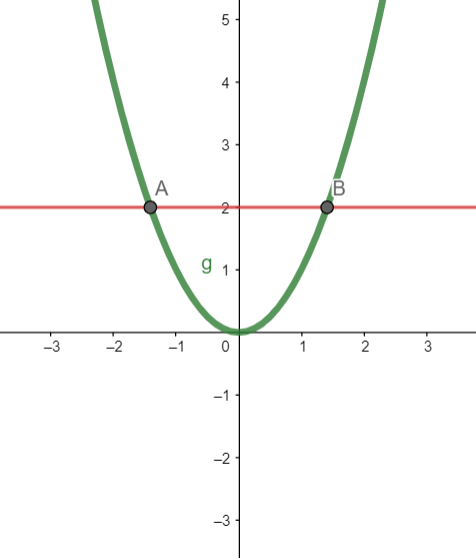
شکل 32-2، تابع $g(x)=x^{2}$ یک به یک نیست زیرا $y=2$ تابع را در دو نقطه قطع کرده است.

2-32 وارون یک رابطه

برای وارون سازی یک رابطه (نه لزوما تابع)، کافی است جای دامنه و برد را عوض کنیم. رابطه زیر را در نظر بگیرید:

$\large k=\{(7,6),(5,8),(7,11)\}$

وارون $k$ را به صورت زیر نمایش می دهیم:

$\large k^{-1}=\{(6,7),(8,5),(11,7)\}$

پس می توانیم وارون یک رابطه را به صورت زیر تعریف کنیم:

(1)

$\large k^{-1}=\{(y,x)|(x,y)\in k\}$

توجه کنید که $k^{-1}$ به معنی $\frac{1}{k}$ نیست.

حال اگر یک تابع را وارون کنیم؛ آیا لزوما وارون آن نیز تابع خواهد بود؟ خیر. تنها در صورتی وارون تابع $f$، تابع خواهد بود که $f$ یک به یک باشد. برای مثال در تابعی، اگر به یک عضو برد، دو عضو دامنه مربوط باشد؛ در وارون این تابع، به یک عضو دامنه، دو عضو برد مربوط خواهد بود که خلاف تعریف ما از تابع بودن است. پس تنها توابعی، وارون پذیرند (وارون آنها نیز تابع است) که یک به یک هستند.

3-32 محاسبه وارون تابع

گاهی وقت ها می توان وارون تابع را به سادگی محاسبه نمود. نگرش تابع به عنوان یک کارخانه سودمند است. کارخانه $f$ پلاستیک را تبدیل به بطری نوشابه می کند و کارخانه $f^{-1}$، بطری نوشابه را بازیافت کرده و دوباره تبدیل به پلاستیک می کند. پس جای ورودی و خروجی در کارخانه وارون تغییر می کند. برای محاسبه وارون تابع نیز همین عمل را پی می گیریم.

* مثال 32-2)

وارون تابع $y=3x-2$ را بدست آورید و نمودار آن را رسم کنید.

پاسخ

تنها کافی است به کارخانه بازیافت فکر کنیم. در اینجا جای متغیر مستقل و وابسته عوض می شود. پس ما باید $x$ را تنها کنیم تا رابطه ای بر حسب $y$ داشته باشیم.

$\large 3x=y+2 \rightarrow x=\frac{y+2}{3}$

چون معمولا دوست داریم تابع وارون را هم مثل تابع اولیه در دستگاه مختصات به شکل $y$ بر حسب $x$ بکشیم؛ کافی است $x$ را با $Y$ جایگذاری نماییم و $y$ را با $X$. در نظر بگیرید بخاطر این $X$ و $Y$ را با حروف بزرگ نمایش دادم که بدانید با $x$ و $y$ سوال دارای تفاوت اند.

$\large Y=\frac{X+2}{3}$

حال نمودار خط بالا را رسم می کنیم:

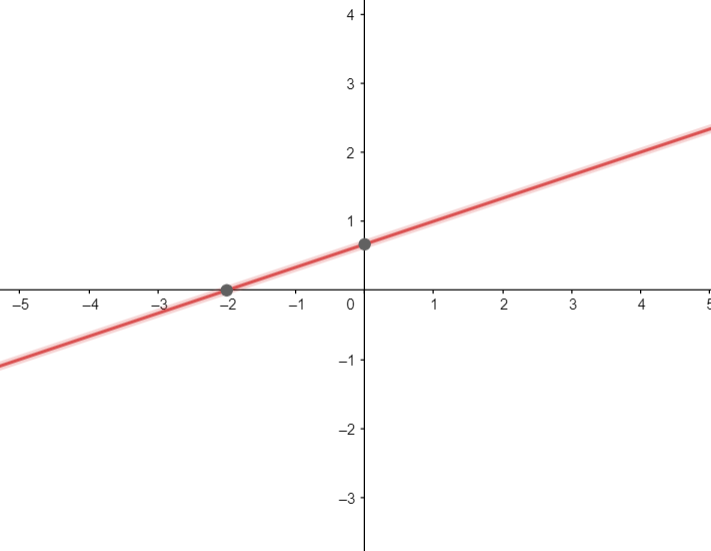
شکل 32-3، نمودار مثال 32-2

4-32 رسم وارون تابع

همانطور که رابطه (1) نشان می دهد، تنها برای بدست آوردن تابع وارون باید جای y هر نقطه را با x آن عوض کنیم. این کار همانند رسم قرینه تابع نسبت به نیمساز ربع اول و سوم است. پس اگر نقطه ای مابین تابع و تابع وارون مشترک باشد؛ لزوما روی نیمساز ربع اول و سوم، یا خط $y=x$ قرار دارد.

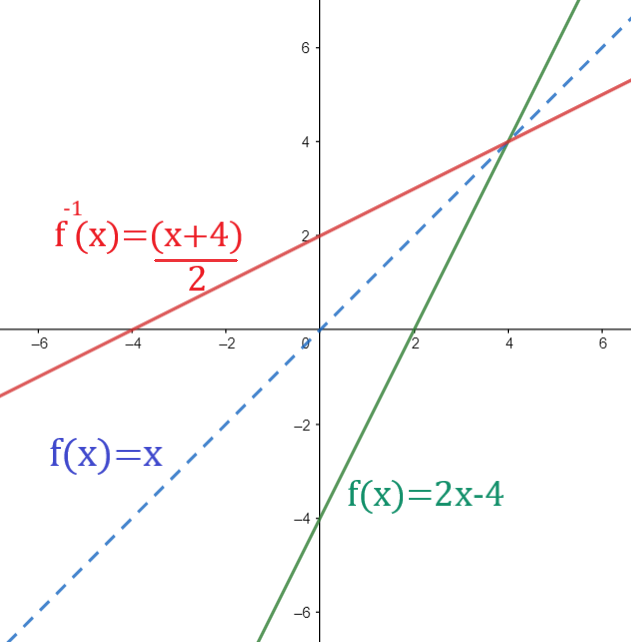
شکل 32-4، تابع $f(x)=2x-4$ و وارون تابع که قرینه آن نسبت به نیمساز ربع اول و سوم است.

5-32 جمع بندی فصل

در این فصل با تابع یک به یک که شرط وارون پذیری تابع بود و وارون تابع آشنا شدیم. رابطه وارون تابع همیشه مثل توابع خطی به سادگی قابل محاسبه نیست اما روش ترسیمی همیشه کاربردی است. برای رسم نمودار در این فصل از بسته نرم افزاری آنلاین جئوجبرا بهره بردم.

*1- می دانیم که $y=x^{2}$ روی دامنه $\mathbb{R}$ وارون پذیر نیست اما با محدود کردن تابع به دامنه هایی خاص می توان این تابع را نیز وارون کرد. وارون $y=x^{2}$ را در دامنه $[0,+\infty )$ محاسبه نمایید.

*2- نقاط مشترک تابع $y=x^{3}$ و وارون آن را محاسبه کنید. (راهنمایی: نیازی به محاسبه تابع وارون نیست)