بسیاری از پدیده ها و توابع در طبیعت، رفتار ساده خطی ندارند. برای مثال اگر سنگی را در نزدیکی زمین، با سرعت پایین پرتاب کنیم؛ مسیری که سنگ طی می کند یک خم است که آن را سهمی می نامیم. این فصل به مطالعه سهمی به عنوان یک تابع اختصاص دارد.

شکل 31-1، انیمیشین پرتاب سنگ، برگرفته از استیکمن فیزیکز

1-31 تعریف

معادله درجه دو را به یاد دارید؟ فرض کنید معادله درجه دومی به صورت زیر داشته باشیم که در آن $y,a,b,c$ معلوم ($a$ نامساوی صفر است) و $x$ مجهول است:

(1)

$\large y=ax^{2}+bx+c $

اینجا یک تفاوت وجود دارد؛ $y$ می تواند مقادیر مختلفی باشد. پس ما می توانیم به ازای هرکدام از این مقادیر معادله درجه دو را حل کنیم که هر معادله می تواند دو، یک یا صفر جواب داشته باشد. سپس در دستگاه مختصات، نقاط $(x,y)$ را مشخص می کنیم. سهمی شکل حاصل کنارهم قرارگرفتن این جواب هاست. این شبیه روشی است که کامپیوتر برای رسم سهمی از آن بهره می برد چون توان محاسباتی بالایی در زمان کوتاه دارد. برای ما رسم سهمی به شکلی تقریبی کافی است.

2-31 تقعر سهمی

سهمی به دو صورت است. رابطه 1 را در نظر بگیرید؛ اگر $a$ مثبت باشد، سهمی رو به بالا است و اگر $a$ منفی باشد سهمی رو به پایین است.:

$\large a>0$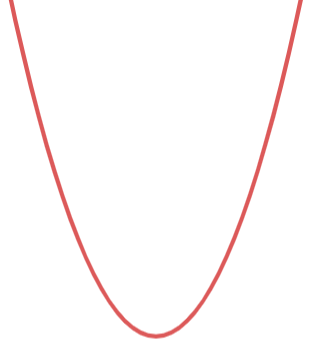
$\large a<0$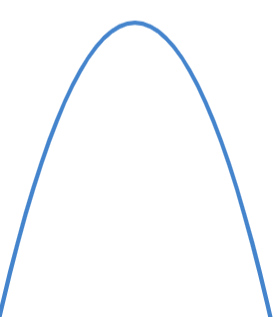

جدول 31-1، تقعر سهمی

3-31 راس سهمی

سهمی شکل متقارن است. به نقطه تقاطع خط تقارن سهمی با سهمی، راس سهمی $A$ گوییم. راس سهمی تنها نقطه ای است که جواب یک معادله درجه دو با یک ریشه است. به یاد داریم از رابطه 13-4، مجموع دو ریشه معادله درجه دوم به صورت $-\frac{b}{a}$ است. چون معادله درجه دومی که حاصل آن راس سهمی است؛ ریشه مکرر (دو ریشه با مقدار یکسان) دارد. پس طول راس سهمی مقدار زیر را دارد:

(2)

$\large x_{A}=-\frac{b}{2a}$

حال کافی است مقدار بالا را در رابطه 1 جایگذاری کنیم تا عرض راس سهمی نیز بدست آید:

(3)

$\large y_{A}=a(-\frac{b}{2a})^{2}+b(-\frac{b}{2a})+c=-\frac{b^{2}}{4a}+c$

بدین ترتیب مختصات راس سهمی بدین صورت است:

(4)

$\large A=(-\frac{b}{2a},-\frac{b^{2}}{4a}+c)$

این نکته هم فراموش نشود که اگر $a>0$، راس سهمی کمترین عرض یا $y$ را در نقاط سهمی دارد. اگر $a<0$، راس سهمی بیشترین عرض را در نقاط سهمی دارد.

* مثال 31-1)

سهمی $y=3x^{2}-2x+4$ را رسم کنید.

پاسخ

معمولا رسم تقریبی را با 3 نقطه انجام می دهیم. راس سهمی، اولین نقطه مورد نیاز است که آن را از رابطه 4 بدست می آوریم:

$\large A=(\frac{1}{3},\frac{11}{3})$

نقطه دومی که خوب است محاسبه کنیم عرض از مبدا سهمی است که همیشه همان $c$ است:

$\large B=(0,4)$

دیگر نقطه، قرینه نقطه B نسبت به خط تقارن سهمی است؛ فاصله هر نقطه در سهمی با خط تقارن، همان طول راس سهمی است. پس آن را دو برابر می کنیم و به طول B اضافه می کنیم. مطمئن هستیم که نقطه قرینه B را یافته ایم:

$\large C=(\frac{2}{3},4)$

حال این سه نقطه را به هم وصل می کنیم:

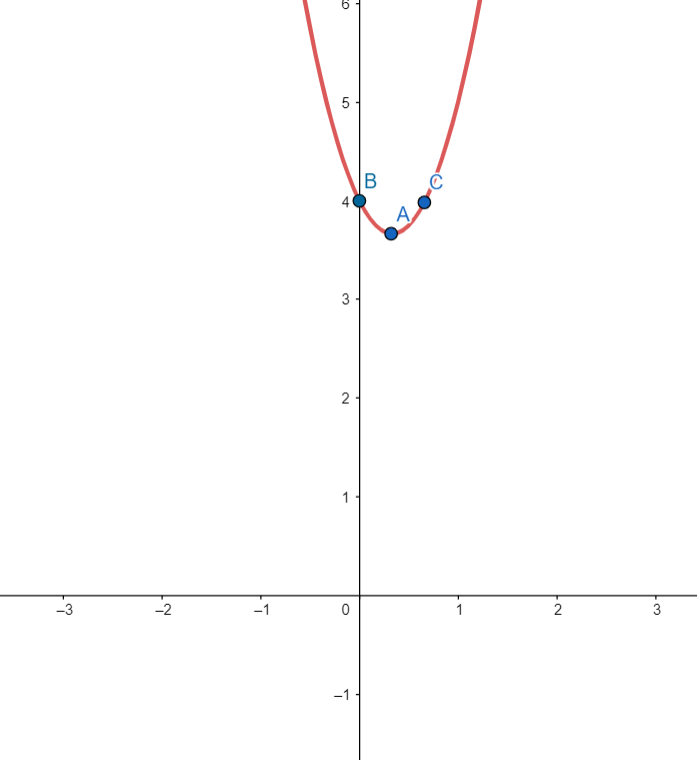
شکل 31-2، مثال 31-1

4-31 جمع بندی فصل

این فصل با سهمی و نحوه رسم آن در دستگاه مختصات آشنا شدیم. در پایان این فصل خوب است به این هم اشاره کنم که هر تابع چندجمله ای که بالاترین درجه آن دو است؛ نمودار آن به شکل سهمی خواهد بود.

*1- سهمی $y=-x^{2}+4x-6$ را رسم کنید.

*2- یک سهمی با محور تقارن $y=-1$ مثال بزنید.