از این فصل، ریاضیات رنگ و بویی جدی تر به خود می گیرد. دو مجموعه A و B را درنظر بگیرید؛ یک تابع از A به B، رابطه ای میان این دو مجموعه است که در آن به هر عضو از A، فقط یک عضو از B نسبت داده می شود. در این جا مجموعه A را دامنه تابع و مجموعه B را برد تابع می نامیم. به چند روش می توان تابع را نمایش داد.

1-30 نمایش نمودار ون و پیکان

در این نحوه نمایش، اعضای مجموعه دامنه را بوسیله پیکان به اعضای مجموعه برد متصل می کنیم. دقت کنید که باید به هر عضو دامنه، حتما یک عضو برد مربوط شود اما برعکس این درست نیست. یک عضو برد می تواند به صفر، یک یا چند عضو دامنه مربوط شود. شکل 30-1، حاوی نکاتی کاربردی در نمایش توابع به این صورت است.

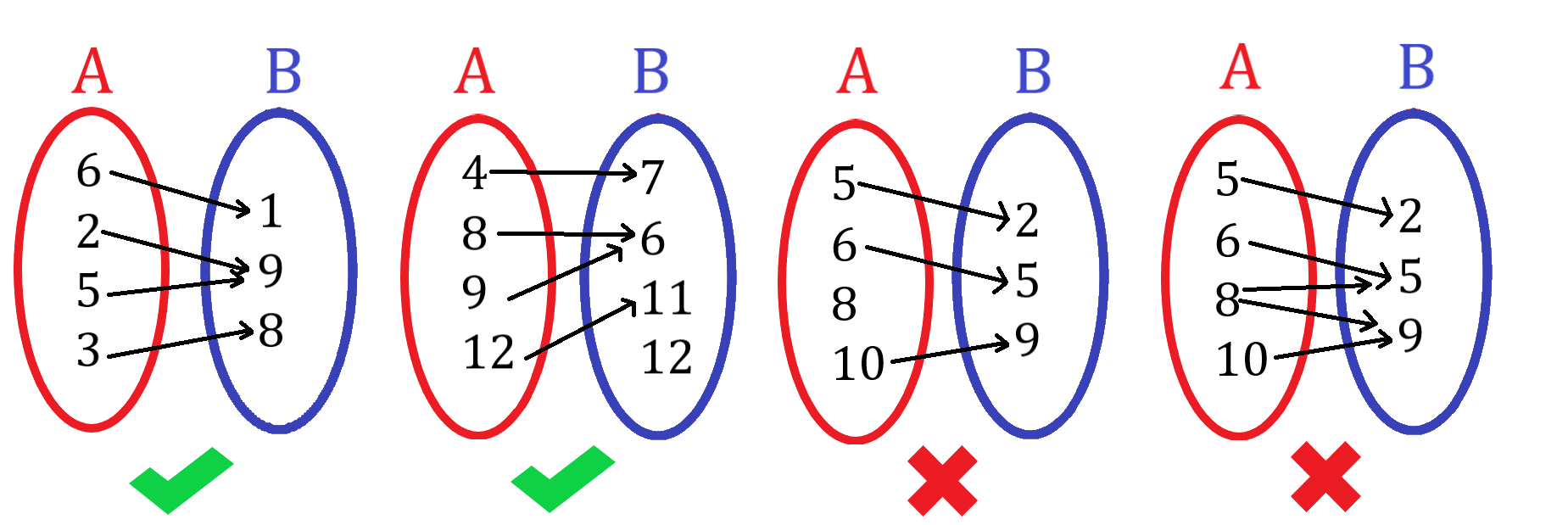
شکل 30-1، از سمت چپ، اولی و دومی تابع هستند و سومی و چهارمی تابع نیستند. در سومی دامنه نمی تواند عضوی داشته باشد که به هیچ عضوی از برد مربوط نباشد. در چهارمی یک عضو دامنه نمی تواند به بیش از یک عضو برد مربوط باشد.

2-30 نمایش زوج مرتبی و نموداری

یکی از نمایش های تابع، نمایش زوج مرتبی $(x,y)$ است؛ به این صورت که هر رابطه میان دامنه و برد را به مانند یک نقطه در دستگاه مختصات نمایش می دهیم. عدد سمت چپ زوج مرتب نشان دهنده عضو دامنه و عدد سمت راست، نشان دهنده عضو برد است. برای مثال در شکل 30-1، تابع سمت چپ را می توان به شکل زیر نمایش داد:

$\large f=\{(6,1),(2,9),(5,9),(3,8)\}$

همانطور که گفتم می توان با چهارعضو تابع بالا، مانند نقاط دستگاه مختصات برخورد کرد. اعضای دامنه مشخصه x و اعضای برد مشخصه y است. نمودار زیر نمایش تابع $f$ است:

شکل 30-2، نمودار تابع $f$

** مثال 30-1)

$x$ را طوری تعیین کنید که $g$ تابع باشد.

$\large g=\{(1,4x-3),(x,5),(2,-4),(1,x^{2})\}$

پاسخ

هر عضو دامنه فقط به یک عضو برد نسبت داده می شود؛ پس تنها باید یک زوج مرتب داشته باشیم که عضو آن از دامنه $1$ است. بدین ترتیب، $4x-3$ و $x^{2}$ با هم برابرند:

$\large x^{2}=4x-3 \rightarrow x^{2}-4x+3=0 \rightarrow $

$\large (x-1)(x-3)=0 \rightarrow x=1,x=3 $

آیا هر دو جواب قابل قبولند؟ خیر! در صورتی که $x=1$ باشد؛ در $g$ هم $(1,1)$ داریم هم $(1,5)$ پس $x$ نمی تواند $1$ باشد. در صورتی که $x=3$ باشد؛ تابع $g$ به صورت زیر در می آید:

$\large g=\{(1,9),(3,5),(2,-4)\}$

$g$ تنها به شرط $x=3$ تابع است.

3-30 نمایش جبری

تابع را می توان به صورت جبری و یک رابطه نمایش داد. در چنین نمایشی، معمولا باید مشخص کنیم که دامنه تابع چیست. دامنه و برد تابع می تواند هرمجموعه متناهی یا نامتناهی از جمله مجموعه اعداد طبیعی و اعداد حقیقی باشد. در این شکل نمایش، ابتدا نامی برای تابع مشخص می کنیم؛ سپس در پرانتزی جلوی نام تابع، نشان می دهیم که تابع، وابسته به چه متغیری است.

(1)

$\large f(x)=2x \; ,\; x \in \mathbb{R} $

در تابع $f(x)$، تابع به متغیر $x$ وابسته است. دامنه تابع نیز مجموعه اعداد حقیقی است. این تابع مانند یک کارخانه، هر عددی از مجموعه اعداد حقیقی را به عنوان ورودی دریافت می کند؛ بر روی آن عملیات ضربدر $2$ انجام می دهد و دو برابر عدد را به عنوان خروجی تحویل ما می دهد. با توجه به اینکه $f(x)$ به ازای هر $x$ که عددی حقیقی باشد خروجی می دهد؛ دیگر نمودار آن به مانند شکل 30-2، گسسته نیست. بلکه بیانگر یک خط است. این بار $f(x)$ را محور $y$ در نظر می گیریم:

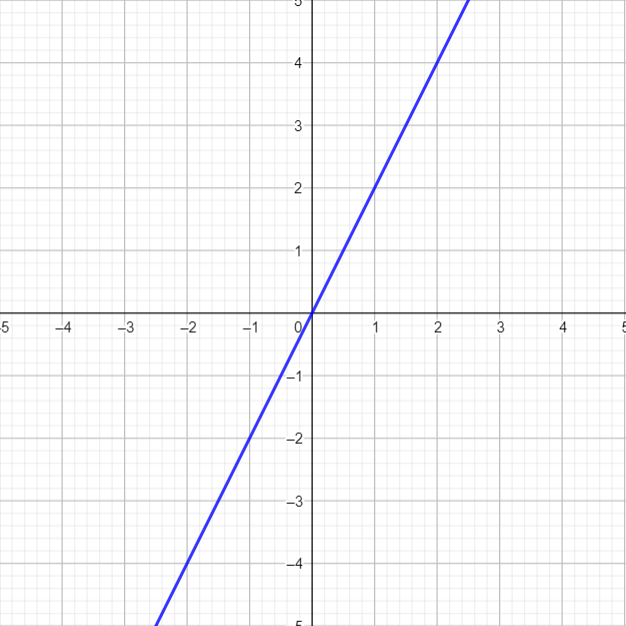
شکل 30-3، نمودار $f(x)=2x$

4-30 جمع بندی فصل

در این فصل با مفاهیم پایه تابع و شیوه های مختلف نمایش آن آشنا شدیم. همچنین مثالی از یک تابع خطی دیدیم. این تنها شکلی از تابع نیست که وجود دارد. توابع مثلثاتی و درجات بالاتر و پایین تر از یک نیز وجود دارند که باید به آن در فصول مجزا بپردازیم. برای نمایش توابع مختلف می توان از بسته های نرم افزاری آنلاین مانند دسموس و جئوجبرا بهره برد.

*1- از دامنه $A=\{1,2\}$ به برد $B=\{3,4\}$، چند تابع می توان نوشت؟

*2- سعی کنید با نقطه یابی نمودار $f(x)=x^{2}$ را رسم کنید. محور تقارن نمودار چه خطی است؟