در این فصل می خواهم به دایره مثلثاتی بپردازم، دایره ای که به محاسبه و درک نسبت های مثلثاتی در زوایای گوناگون کمک می کند.
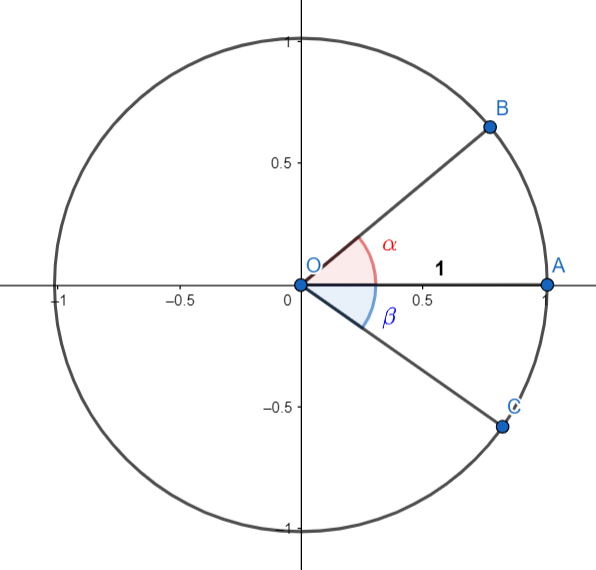
شکل 29-1، دایره مثلثاتی
1-29 تعریف
دایره ای مطابق شکل 29-1، در نظر بگیرید. همانطور که در تصویر می بینید؛ پاره خط $OA$ همان شعاع دایره است. طول این شعاع را یک در نظر می گیریم. همچنین مرکز این دایره، مبدا مختصات است. معمولا برای پیمایش روی این دایره، از نقطه $A$ شروع می کنیم. بگذارید همین ابتدا یک قرارداد امضا کنیم؛ ساعت ها اشیائی منفی اند. این به چه معنی است؟ اگر در جهت عقربه های ساعت حرکت کنیم (مثلا انگار که از ساعت 3 به ساعت 4 می رویم) و از نقطه $A$ به نقطه $C$ برسیم. زاویه روبه روی این مسیر پیموده شده، که در اینجا $\beta$ نامیدیم؛ منفی است. اگر خلاف جهت عقربه های ساعت حرکت کردیم و از نقطه $A$ به نقطه $B$ رسیدیم. زاویه مدنظر ما که در اینجا $\alpha$ نامیدیم. مثبت است. برای مثال اگر $+90$ درجه حرکت کنیم یا $-270$؛ به یک نقطه می رسیم:
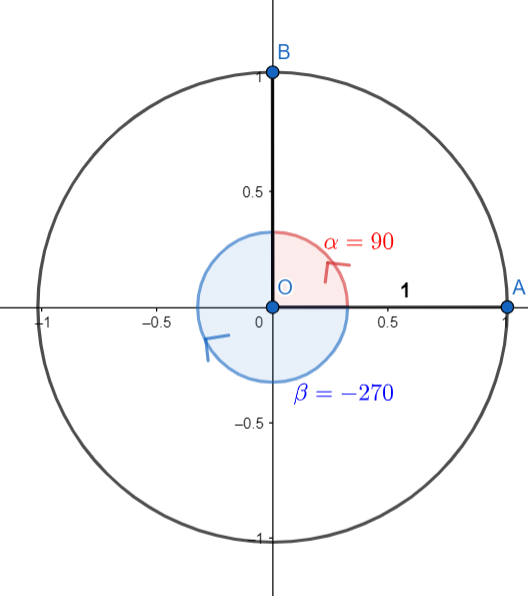
شکل 29-2، نمایش دو زاویه $+90$ و $-270$ بر دایره
2-29 نسبت های مثلثاتی
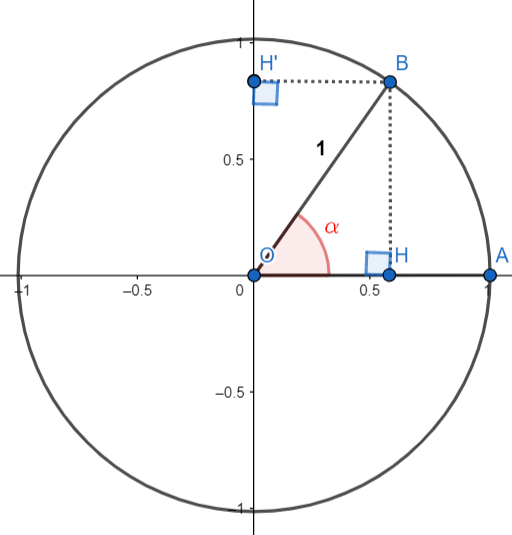
شکل 29-3
هدف از ساخت دایره مثلثاتی، محاسبه نسبت های مثلثاتی است. شکل 29-3 را در نظر بگیرید؛ مثلث $BOH$ یک مثلث قائم الزاویه با طول وتر 1 است که همان شعاع دایره می باشد($OB=1$). نسبت مثلثاتی سینوس برای زاویه $\alpha$ به صورت زیر است:
(1)
$\large \sin(\alpha)=\frac{HB}{OB}=HB $
پس تصویر نقطه $B$ بر روی محور y در دایره مثلثاتی، سینوس زاویه $\alpha$ است. نسبت مثلثاتی کسینوس نیز برای زاویه $\alpha$ به صورت زیر است:
(2)
$\large \cos(\alpha)=\frac{OH}{OB}=OH $
بدین ترتیب تصویر نقطه $B$ بر روی محور x در دایره مثلثاتی، سینوس زاویه $\alpha$ است. تانژانت $\alpha$ شیب خط $OB$ است که از رابطه زیر قابل محاسبه است:
(3)
$\large \tan(\alpha)=\frac{HB}{OH}$
* مثال 29-1)
نسبت های مثلثاتی زاویه $\frac{\pi}{2}-\alpha$ را برحسب نسبت های مثلثاتی زاویه $\alpha$ محاسبه نمایید.
پاسخ
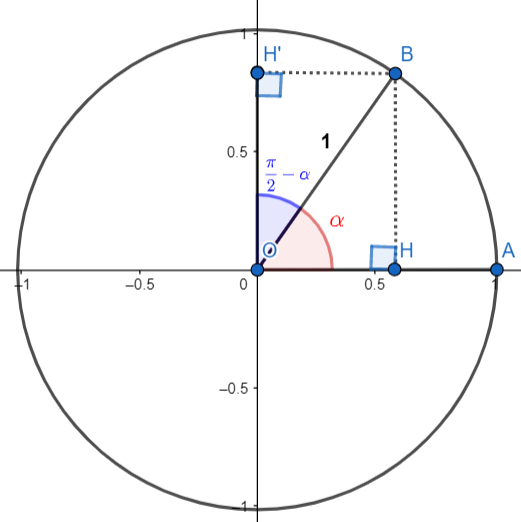
شکل 29-4، مثال 29-1
با استفاده از مثلث قائم الزاویه $BOH’$، نسبت های مثلثاتی $\frac{\pi}{2}-\alpha$ را محاسبه می کنیم و البته برابری تصویر نقطه B روی دو محور و پاره خط های موازی را درنظر می گیریم:
$\sin(\frac{\pi}{2}-\alpha)=H’B=OH\rightarrow \sin(\frac{\pi}{2}-\alpha)=\cos(\alpha)$
$\cos(\frac{\pi}{2}-\alpha)=OH’=HB\rightarrow \cos(\frac{\pi}{2}-\alpha)=\sin(\alpha)$
$\tan(\frac{\pi}{2}-\alpha)=\frac{1}{\tan(\alpha)}=\cot(\alpha)$
* مثال 29-2)
نسبت های مثلثاتی زاویه $-\alpha$ را محاسبه کنید.
پاسخ
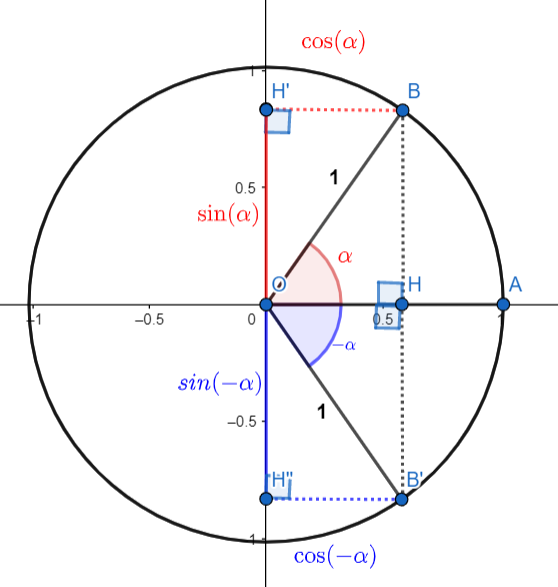
شکل 29-5، مثال 29-2
همانطور که در شکل 29-5 می بینید؛ با قرینه شدن زاویه، سینوس هم قرینه می شود اما کسینوس تغییر علامت نمی دهد:
$\sin(-\alpha)=-\sin(\alpha)$
$\cos(-\alpha)=\cos(\alpha)$
3-29 ربع های دایره مثلثاتی
می توان چهاربخش در دایره مثلثاتی مشخص کرد که در هرکدام از این بخش ها، علامت نسبت های مثلثاتی با هم یکسان باشد. این ربع ها را خلاف جهت عقربه های ساعت نامگذاری می کنیم. در شکل 29-3، نقطه $B$ و زاویه $\alpha$ را در نظر بگیرید؛ یک پیمایش کامل بر روی دایره مثلثاتی در جهت ساعتگرد یا پادساعتگرد، $2\pi$ به اندازه زاویه اضافه یا کم می کند؛ اما جایگاه نقطه B را تغییر نمی دهد. پس اضافه شدن مضرب صحیحی از $2\pi$ به هر زاویه، نسبت های مثلثاتی را تغییر نمی دهد. این را می توان از رابطه 17-1 و 17-2 نیز به سادگی اثبات کرد؛ برای مثال من این کار را برای سینوس $\alpha + 2k\pi$ انجام می دهم:
$\large \sin(\alpha + 2k\pi)=\sin(\alpha)\cos(2k\pi)+\sin(2k\pi)\cos(\alpha)=\sin(\alpha)$
در جدول زیر، اطلاعات محدوده چهار ربع دایره و تصویر آن ها را آورده ام ($k \in \mathbb{Z}$):
| ربع | محدوده ربع به رادیان | محدوده ربع به درجه | تصویر |
| اول | $0+2k\pi<\alpha<\frac{\pi}{2}+2k\pi$ | $0+360k<\alpha<90+360k$ | 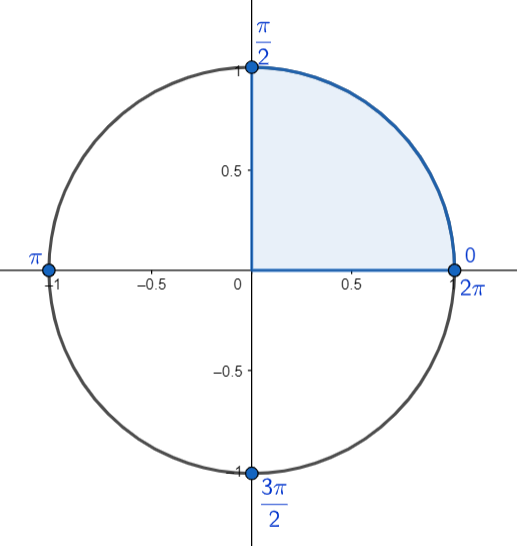 |
| دوم | $\frac{\pi}{2}+2k\pi<\alpha<\pi+2k\pi$ | $90+360k<\alpha<180+360k$ | 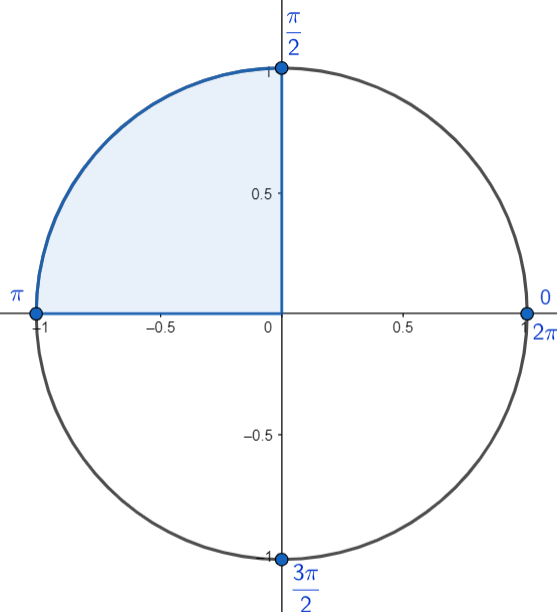 |
| سوم | $\pi+2k\pi<\alpha<\frac{3\pi}{2}+2k\pi$ | $180+360k<\alpha<270+360k$ | 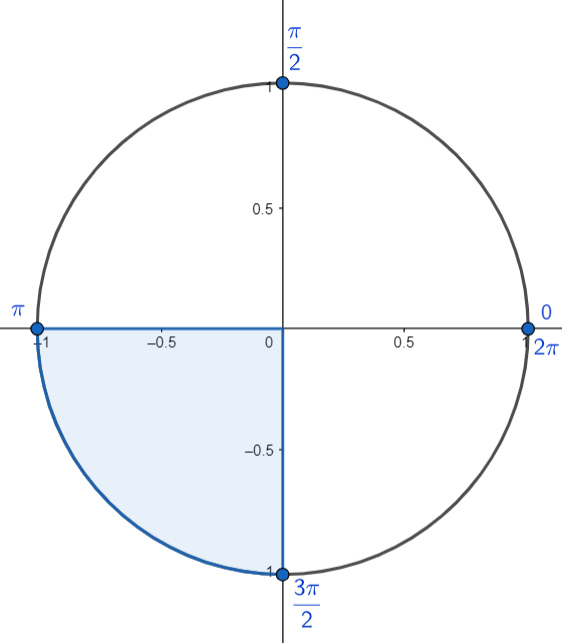 |
| چهارم | $\frac{3\pi}{2}+2k\pi<\alpha<2\pi+2k\pi$ | $270+360k<\alpha<360+360k$ | 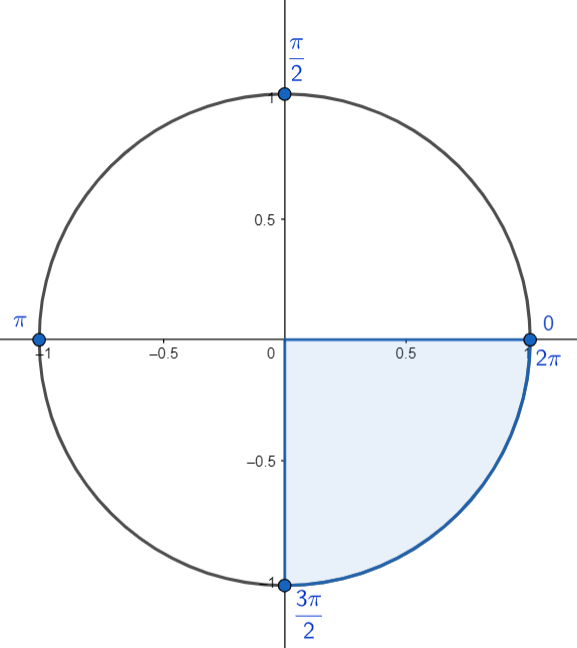 |
جدول 29-1، محدوده هر ربع دایره مثلثاتی
در جدول زیر، اطلاعات مربوط به علامت نسبت های مثلثاتی در هر یک از چهار ربع مثلثاتی و مقدار این نسبت ها در مرز ربع ها را آورده ام؛ علامت نسبت های مثلثاتی در دایره مثلثاتی، معمولا با واژه “هستک” بخاطر سپرده می شود که به معنی مثبت بودن همه در ربع اول، مثبت بودن سینوس در ربع دوم، مثبت بودن تانژانت در ربع سوم و مثبت بودن کسینوس در ربع چهارم می باشد:
| ربع یا مرز | علامت یا مقدار سینوس | علامت یا مقدار کسینوس | علامت یا مقدار تانژانت |
| $0$ | $0$ | $1$ | $0$ |
| ربع اول | $+$ | $+$ | $+$ |
| $\frac{\pi}{2}$ | $1$ | $0$ | تعریف نشده |
| ربع دوم | $+$ | $-$ | $-$ |
| $pi$ | $0$ | $-1$ | $0$ |
| ربع سوم | $-$ | $-$ | $+$ |
| $\frac{3\pi}{2}$ | $-1$ | $0$ | تعریف نشده |
| ربع چهارم | $-$ | $+$ | $-$ |
| $2\pi$ | $0$ | $1$ | $0$ |
جدول 29-2، علامت نسبت های مثلثاتی در ربع ها و مقدار آن ها در مرز
4-29 جمع بندی فصل
در این فصل نسبتا پر و پیمان، با دایره مثلثاتی آشنا شدیم. تمرینات پایان فصل را از دست ندهید؛ این تمرینات درک بهتری از نسبت های مثلثاتی به شما خواهد داد.
| تمرینات فصل |
*1- با استفاده از جدول 29-2 و رابطه 17-1 و 17-2، ثابت کنید:
$\large \sin(\frac{\pi}{2}+b)=\cos(b)$
$\large \cos(\frac{\pi}{2}+b)=-\sin(b)$
$\large \sin(\pi-b)=\sin(b)$
ترتیب فصل |
قبلی |
فعلی |
بعدی |
عنوان |
28 بازه |
29 دایره مثلثاتی |
30 تابع : نمایش |




