در فصل 15، با اتحادهای مثلثاتی که نتیجه قضیه فیثاغورث بودند؛ آشنا شدیم. این بار می خواهم با نوعی دیگر از اتحادهای مثلثاتی آشنا شویم. اتحادهایی که بیانگر جمع دو زاویه در آرگومان نسبت های مثلثاتی است. مثلا با دانستن نسبت های مثلثاتی زوایای $a$ و $b$ می توان نسبت های مثلثاتی زاویه $a+b$ را یافت.

1-17 سینوس و کسینوس جمع دو زاویه

مستطیل شکل 17-1 را در نظر بگیرید، هدف محاسبه $\sin(a+b)$ است؛ تنها فرض این شکل، همان خطی است که اندازه ای برابر با یک دارد.

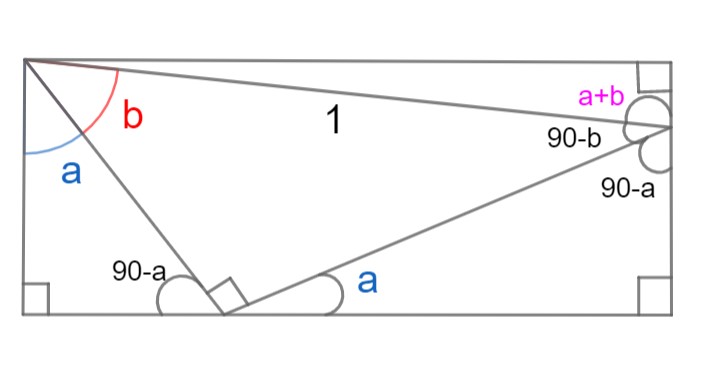
شکل 17-1، دو زاویه a و b با رنگ آبی و قرمز مشخص شدند

حال می توان در مثلث قائم الزاویه ای که زاویه b قرار دارد، به سادگی طول دو ضلع دیگر را مشخص کرد، $\sin(b)$ نسبت ضلع روبه روی زاویه b به وتر است که طولی برابر با یک دارد. پس ضلع روبرو به زاویه b همان $\sin(b)$ است و ضلع مجاور $\cos(b)$:

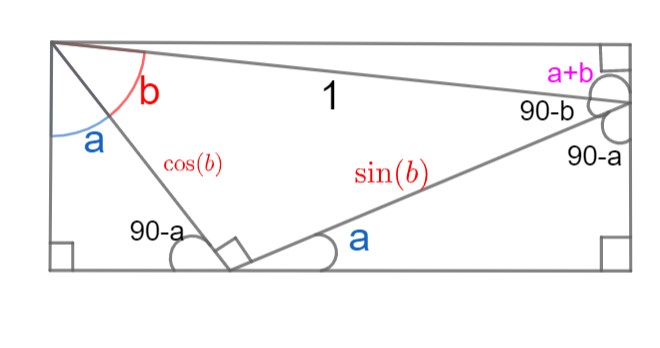
شکل 17-2، اندازه دو ضلع مذکور مشخص شد

حال مثلث قائم الزاویه سمت چپ را در نظر بگیرید که شامل زاویه a است. می دانیم که وتر این مثلث $\cos(b)$ است. ضلع روبه روی زاویه a، به سادگی برابر با $\sin(a)\cos(b)$ است. همچنین ضلع مجاور را نیز از $\cos(a)$ به راحتی محاسبه می کنیم. این ضلع برابر است با $\cos(a)\cos(b)$. مشابه همین روند را برای قائم الزاویه پایین سمت راست تصویر انجام می دهم؛ حاصل در شکل 17-3 به تصویر کشیده شده:

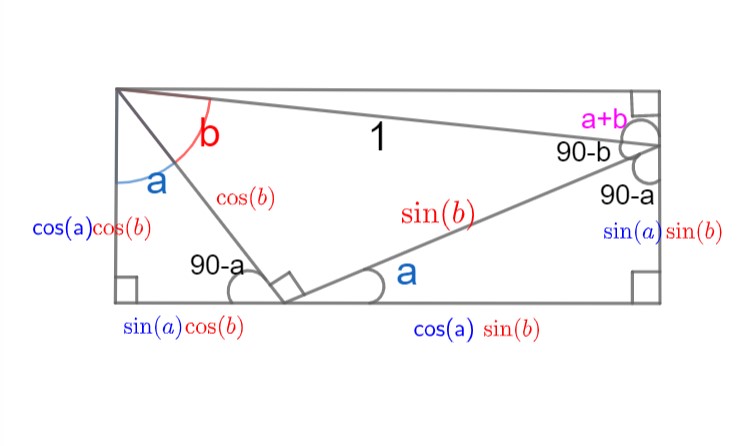
شکل 17-3، اضلاع دو مثلث مذکور مشخص شد

حال اگر نیک بنگرید، مسئله را حل شده می یابید! در مستطیل ضلع بالا با ضلع پایین برابر است؛ پس به سراغ مثلث بالا که شامل a+b است می رویم؛ تنها کافی است $\sin(a+b)$ را در این مثلث بیابیم. ضلع بالا را تقسیم بر وترمان می کنیم که طولی برابر با یک دارد؛ نتیجه همان ضلع پایینی مستطیل است:

(1)

$\large \sin(a+b)=\sin(a)\cos(b)+\sin(b)\cos(a)$

اگر ضلع به طول $\cos(a)cos(b)$ مثلث راست را از ضلع به طول $\sin(a)sin(b)$ کم کنید؛ چون وتر مثلث بالایی برابر با یک است؛ همین طول را می توان $\cos(a+b)$ نامید:

(2)

$\large \cos(a+b)=\cos(a)\cos(b)-\sin(b)\sin(a)$

2-17 سینوس و کسینوس دو برابر زاویه

از رابطه (1) و (2) می توان شرایطی را بررسی کرد که $a=b$ باشد؛ در این صورت می توان نسبت های مثلثاتی $2a$ را از نسبت های مثلثاتی $a$ محاسبه نمود؛ رابطه یک به صورت زیر در می آید:

(3)

$\large \sin(2a)=2\sin(a)\cos(a)$

و همچنین رابطه (2) به شکل زیر تبدیل می شود:

(4)

$ \large \cos(2a)=\cos^{2}(a)-\sin^{2}(a) $

* مثال 17-1)

از نسبت های مثلثاتی $\frac{\pi}{2}$، نسبت های مثلثاتی سینوس و کسینوس $\pi$ را محاسبه کنید.

پاسخ

از رابطه (3) داریم:

$\large \sin(2\frac{\pi}{2})=\sin(\pi)=2\sin(\frac{\pi}{2})\cos(\frac{\pi}{2})=0$

همچنین از رابطه (4) کسینوس را محاسبه می کنم:

$\large \cos(\pi)=\cos^{2}(\frac{\pi}{2})-\sin^{2}(\frac{\pi}{2})=0-1=-1$

3-17 جمع بندی فصل

در این فصل با فرمول بندی اتحادهای مثلثاتی برای جمع دو زاویه آشنا شدیم؛ برای تعداد زوایای بیشتر هم به سادگی می توان به همین روابط مراجعه کرد؛ برای تمرین در این زمینه، محاسبه تانژانت جمع دو زاویه و دو برابر زاویه را در تمرین 17-1 و 17-2 به شما سپردم. برای تصویرسازی از وبسایت جئوجبرا بهره بردم.

*1- رابطه تانژانت جمع دو زاویه به صورت زیر است؛ آن را اثبات کنید:

(5)

$\Large \tan(a+b)=\frac{\tan(a)+\tan(b)}{1-\tan(a)\tan(b)}$

(راهنمایی: می دانید که $\tan(x)=\frac{\sin(x)}{\cos(x)}$، از این جمله و رابطه (1) و (2) بهره ببرید و صورت و مخرج را بر عبارتی تقسیم کنید تا جمله اول مخرج یک بشود)

*2- رابطه تانژانت دو برابر زاویه به صورت زیر است؛ آن را اثبات کنید:

(6)

$\Large \tan(2a)=\frac{2\tan(a)}{1-\tan^{2}(a)}$