در این فصل، قصد داریم تا با یکایی دیگر برای معرفی زاویه آشنا شویم. همانطور که می دانید، درجه مشهورترین یکایی است که برای مقداردهی به زوایا می شناسیم. درجه، به طور قراردادی، $\frac{1}{360}$ زاویه ای است که یک دایره را به طور کامل دور می زند. حال در اینجا قصد دارم یکایی دیگر، شبیه درجه معرفی کنم که در محاسبات علمی و نظری کاربرد بیشتری دارد. این یکا رادیان است.

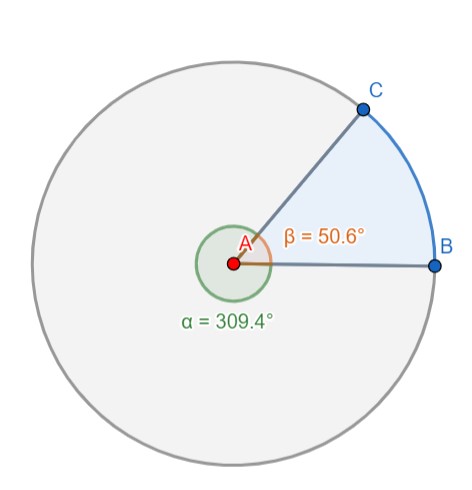
شکل 16-1، یک دایره به دو کمان تقسیم شده، اگر از B شروع کرده و به صورت پادساعتگرد، روی محیط دایره حرکت کنیم تا به نقطه B بازگردیم؛ از منظر زاویه ای 360 درجه پیموده ایم.

1-16 تعریف

در مورد رادیان تعاریف گوناگونی آمده اما من صرفا به عنوان یک یکا برای بیان زاویه به آن نگاه می کنم. دایره و محیط و طول کمان آن، می تواند شهود خوبی به شما بدهد؛ رابطه محیط دایره ای به شعاع r، به صورت زیر است:

(1)

$\Large P=2\pi r$

خیلی جالب می شود اگر بدانید که طول کمانی روی همین دایره، تنها وابسته به شعاع و زاویه مابین کمان (البته به یکای رادیان) است؛ پس مزیت تعریف رادیان همین درک ساده از طول کمان دایره خواهد بود.

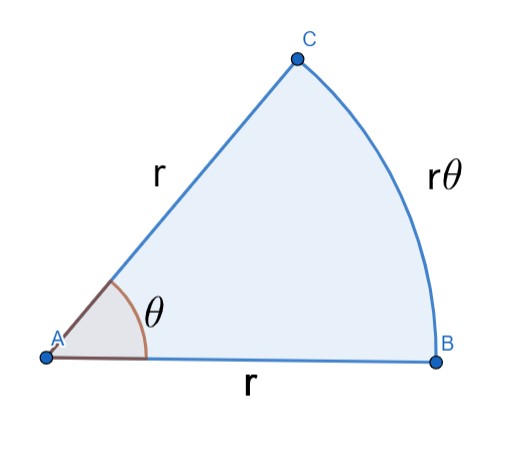شکل 13-2، کمان روبروی زاویه $\theta$

طول کمان روبروی زاویه $\theta$ بر روی دایره ای به شعاع $r$، مطابق شکل 13-2، به صورت زیر است:

(2)

$\Large L=r\theta$

حال دیگر مقدمه چینی کافی است؛ مطابق رابطه (2)، 1 رادیان زاویه ای است که طول کمان روبه روی آن برابر با شعاع دایره باشد. اگر در رابطه بالا $\theta$ را برابر با یک بگذارید، جمله قبلی را نتیجه می گیرید. حالا قابل درک است که $\theta=2\pi$ زاویه ای است که کمان روبروی آن، همان محیط دایره می باشد.

2-16 تبدیل درجه به رادیان

کلید تبدیل درجه به رادیان، همان محیط دایره و اندازه زاویه 360 درجه یا $2\pi$ رادیان است. برای من نوشتن یک کسر تبدیل ساده ترین کار است، اما می توان این تبدیل را به صورت رابطه زیر درآورد؛ ضمن اینکه می دانیم نیم صفحه در دو یکا برابر با 180 درجه و $\pi$ است:

(3)

$\Large \frac{\theta_{rad}}{\pi}=\frac{\theta_{deg}}{180}$

* مثال 16-1)

یک رادیان چند درجه است؟

پاسخ

از رابطه (3) استفاده می کنیم:

$ \frac{1}{\pi}=\frac{\theta_{deg}}{180}$

عدد پی را $\pi=3.14$ در نظر گرفتم و زاویه به درجه بدست می آید:

$\theta_{deg}=\frac{180}{3.14}\approx 57^{\circ}$

3-16 جمع بندی فصل

در این فصل با مفهوم رادیان و تبدیل درجه و رادیان به یکدیگر آشنا شدیم. البته یکاهای دیگری همچون گرادیان، دور و… نیز برای بیان زاویه وجود دارد که می توان آن ها را نیز در فرصتی دیگر بیان نمود. با تبدیل زوایای مشهور به رادیان آشنا شوید چون در مثلثات کاربردی است؛ به همین جهت تمرین 16-1 را برایتان قراردادم.

*1- زوایای 30،45،60،90،270 درجه را به رادیان تبدیل کنید.