در فصل 12، نسبت های مثلثاتی را شناختیم. در مثلثات هم اتحادهایی داریم که در محاسبات مختلف، یاور ما خواهند بود و میان نسبت های مثلثاتی، پل هایی کاربردی ایجاد می کنند. اتحاد های مثلثاتی گاهی به سادگی و گاهی به دشواری اثبات می شوند اما نکته مهم به خاطر سپردن برخی از آنها است. همچنین در مثلثات، راه میانبری هنوز اختراع نشده و تکرار و تمرین زیاد برای یادگیری بسیار راهگشاست. در این فصل، بیشتر به اتحادهایی می پردازیم که از قضیه فیثاغورث نشات می گیرند.

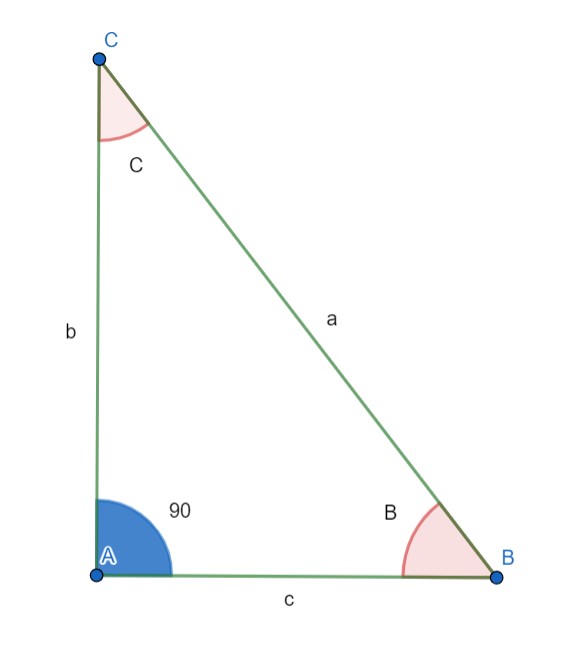
شکل 15-1، مثلث قائم الزاویه

1-15 اتحاد مثلثاتی سینوس و کسینوس

در این بخش می خواهم تمرین 11-1 را اثبات کنم، باز هم شکل تکراری 15-1، را در نظر بگیرید و خوب به محاسبات زیر دقت کنید. قضیه فیثاغورث و رابطه مثلثاتی سینوس و کسینوس فرضیات ما برای این اثبات هستند:

$\Large \displaylines{\sin(B)=\frac{b}{a} \\ \cos(B)=\frac{c}{a} \\ b^2+c^2=a^2}$

حال دوطرف تساوی قضیه فیثاغورث را بر $a^2$، تقسیم می کنیم:

$\Large \frac{ b^2}{a^2}+\frac{c^2}{a^2}=1$

مشخص است که دو جمله سمت چپ، سینوس و کسینوس به توان دو هستند پس:

(1)

$\Large \sin^{2}(B)+\cos^{2}(B)=1$

اولین اتحاد مثلثاتی ما، نتیجه قضیه فیثاغورث است و به ازای هر زاویه ای برقرار می باشد.

* مثال 15-1)

در صورتی که $\sin(\theta)=\frac{\sqrt{2}}{2}$ باشد، $\cos(\theta)$ را محاسبه کنید.

پاسخ

از رابطه (1) استفاده کنیم:

$\Large \displaylines{\frac{1}{2}+\cos^{2}(\theta)=1 \\ \cos(\theta)=\pm \frac{\sqrt{2}}{2}}$

کسینوس می تواند منفی هم باشد؟ بله! مفهوم نسبت های مثلثاتی به زوایای بیش از 90 درجه یا کمتر از 0 درجه نیز قابل تعمیم است و امکان دارد نسبت های مثلثاتی منفی باشند.

2-15 اتحاد مثلثاتی سینوس و کتانژانت

دیگر ارتباط مشهور میان نسبت های مثلثاتی، رابطه سینوس و کتانژانت است؛ بیاید با هم این اتحاد مثلثاتی را محاسبه کنیم، بازهم شکل 15-1 را در نظر بگیرید:

$\Large \cot^2(B)=\frac{c^2}{b^2}$

به دو طرف عبارت 1 اضافه می کنیم و در سمت راست تساوی، مخرج مشترک می گیریم:

$\Large 1+\cot^2(B)=\frac{b^2+c^2}{b^2}$

قضیه فیثاغورث، صورت کسر سمت راست تساوی را بدست می دهد:

$\Large 1+\cot^2(B)=\frac{a^2}{b^2}$

عبارت سمت راست تساوی، معکوس سینوس به توان دو نیست؟چرا، حال دیگر اثباتمان کامل شده:

(2)

$\Large 1+\cot^2(B)=\frac{1}{\sin^2(B)}$

یک اتحاد مثلثاتی مشهور دیگر، رابطه فیثاغورثی کسینوس و تانژانت است که اثبات آن را به شما در تمرین 15-1 می سپارم. این اتحاد نیز به صورت زیر است:

(3)

$\Large 1+\tan^2(B)=\frac{1}{\cos^2(B)}$

اگر جایی به جای سینوس و کسینوس، کسکانت و سکانت دیدید نگران نباشید؛ سینوس معکوس کسکانت و کسینوس معکوس سکانت است.

3-15 جمع بندی فصل

در این فصل، درهم آمیختن قضیه فیثاغورث و نسبت های مثلثاتی، سه رابطه زیبا را به ما هدیه داد. اثبات این سه قضیه ساده بود اما همیشه با این روابط در علوم مهندسی و فیزیکی سروکار خواهید داشت. باز هم تاکید می کنم که اینجا حافظه نقش مهمی را بازی می کند!

*1- رابطه (3) را اثبات کنید.