در تمرین 11-1، گریزی به مفهوم نسبت های مثلثاتی زدیم. در این مقاله قصد معرفی تمامی نسبت های مثلثاتی را دارم. نسبت های مثلثاتی، حاصل تقسیم طول یکی از اضلاع مثلث قائم الزاویه به دیگر ضلع است؛ از آن جایی که 3 ضلع داریم، این انتظار را داریم که 6 نسبت مثلثاتی داشته باشیم. مشهور است که برای رصدهای نجومی، اولین بار، هیپارخوس(ابرخس) یونانی جدول های مثلثاتی را برای زوایای گوناگون تهیه نموده.

شکل 12-1، هیپارخوس نیقیه ای (190 پیش از میلاد – 120 پیش از میلاد)

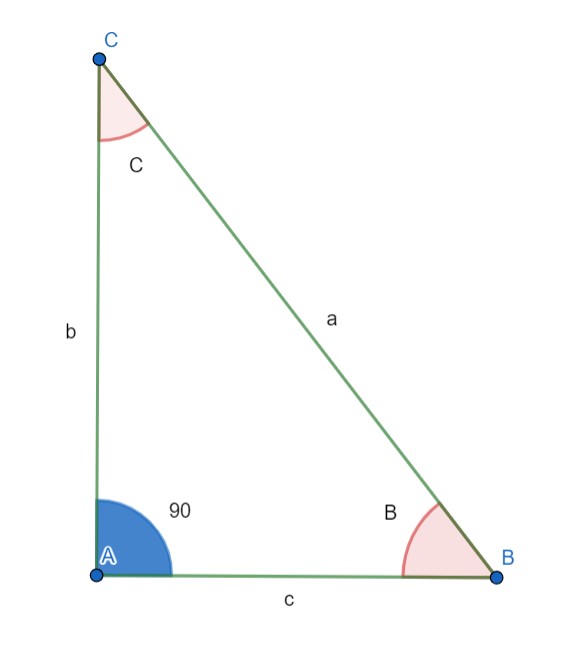
شکل 12-2، مثلث قائم الزاویه

1-12 سینوس

معروف ترین نسبت مثلثاتی سینوس است. شکل 12-2 را درنظر بگیرید؛ سینوس هر زاویه در مثلث قائم الزاویه، نسبت طول ضلع روبه روی آن زاویه به طول وتر مثلث است؛ برای زاویه B داریم:

(1)

$\Large \sin(B)=\frac{b}{a}$

* مثال 12-1)

به شکل 12-2 نگاه کنید؛ اگر زاویه B نزدیک به 90 درجه باشد؛ سینوس این زاویه چقدر خواهد بود؟

پاسخ

با شهود این که زاویه B به سمت 90 درجه می رود؛ پس ضلع c به سمت صفر حرکت خواهد کرد و انگار دو ضلع a و b قصد دارند برهم منطبق و هم اندازه شوند؛ با توجه به رابطه (1) داریم:

$\Large \sin(B)=\frac{b}{a} \approx 1$

پس یک سینوس یک زاویه خوب و مهم را (با استدلالی نه چندان محکم اما مشهود) محاسبه کردیم:

(2)

$\Large \sin(90^{\circ})=1$

2-12 کسینوس

نسبت مثلثاتی کسینوس، حاصل تقسیم طول ضلع مجاور(کناری) زاویه به طول وتر است؛ برای زاویه B داریم:

(3)

$\Large \cos(B)=\frac{c}{a}$

از قضیه فیثاغورث، تمرین 11-1 و رابطه 11-4 می دانیم:

(4-11)

$\Large \sin(B)^{2}+\cos(B)^{2}=1$

پس با توجه به رابطه (2)، می توان $\cos(90^{\circ})$ را محاسبه نمود:

(4)

$\Large \cos(90^{\circ})=0$

شبیه به استدلالی که در مثال 1 کردیم؛ می توان برای ضلع روبه روی زاویه C انجام داد و نتیجه زیر را گرفت:

(5)

$ \Large  \sin(0^{\circ})=0 $

$ \Large \cos(0^{\circ})=1 $

3-12 تانژانت

دیگر نسبت مهم مثلثاتی، تانژانت است. تانژانت نسبت طول ضلع روبه رو به طول ضلع مجاور است. اگر فصل 8 معادله خط را به یاد داشته باشید؛ می توان تانژانت زاویه ای که خط با محور x ها می ساخت را شیب خط دانست. برای زاویه B این نسبت به صورت زیر است:

(6)

$\Large \tan(B)=\frac{b}{c}$

از رابطه (1)،(3) و (6) به سادگی می توان رابطه زیر را استخراج نمود:

(7)

$\Large \tan(B)=\frac{\sin(B)}{\cos(B)}$

4-12 دیگر نسبت های مثلثاتی

سه نسبت مثلثاتی اصلی همان هایی بودند که معرفی کردم؛ سه نسبت دیگر فقط معکوس آنهاست. آنها را به صورت زیر معرفی می کنم:

کتانژانت

(8)

$\Large \cot(B)=\frac{1}{\tan(B)}$

سکانت

(9)

$\Large \sec(B)=\frac{1}{\cos(B)}$

کسکانت

(10)

$\Large \csc(B)=\frac{1}{\sin(B)}$

5-12 جمع بندی فصل

نسبت های مثلثاتی را تعریف کردیم و با آنها آشنا شدیم؛ فکر می کنم از روابط بالا واضح است که با دانستن یکی از نسبت های مثلثاتی، تمامی نسبت های دیگر قابل محاسبه اند. مثلثات را خوب بشناسید که کاربرد آن بسیار است.

*1- تمامی نسبت های مثلثاتی $0$ و $90$ درجه را محاسبه نمایید.

*2- ثابت کنید $\tan(B)\cot(B)=1$