در فصل 10، تمرین 2 گریزی به قضیه فیثاغورث زدیم. بنظرم این قضیه آن قدر مهم و محترم است که باید در یک مقاله جدا نیز به آن پرداخت! قضیه فیثاغورث طول دو ضلع قائمه مثلث قائم الزاویه را به طول وتر آن مربوط می کند. ممکن است در اینترنت فیثاغورس نیز ببینید اما بنظرم فیثاغورث زیباتر است!

شکل 11-1، مجسمه فیثاغورث، فیلسوف و ریاضی دان یونانی(570 ق.م – 495 ق.م)

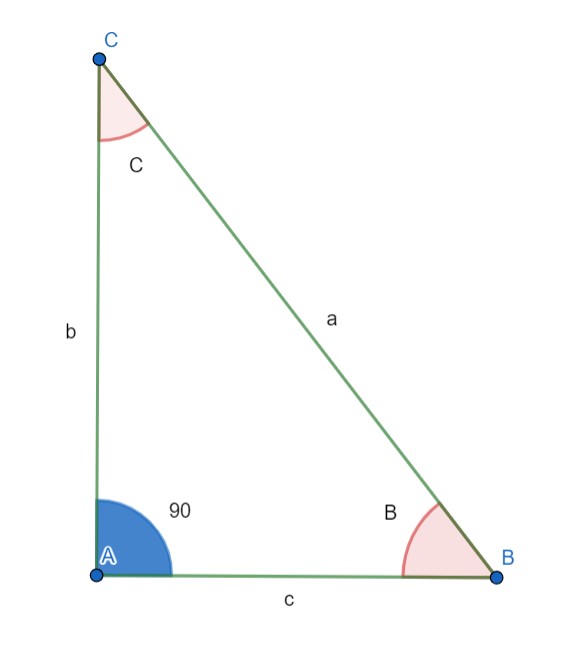
شکل 11-2، مثلث قائم الزاویه

1-11 تعریف

شکل 11-2 را در نظر بگیرید؛ می دانیم که مساحت هر مربع، طول ضلع مربع به توان دو است؛ قضیه این را به ما می گوید که اگر یک مربع با ضلعی به طول $b$ و مربع دیگری با ضلعی به طول $c$ داشته باشیم؛ مجموع مساحت این دو مربع؛ برابر با مجموع مساحت یک مربع با ضلعی به طول $a$ است:

(1)

$\Large a^2=b^2+c^2$

بدین ترتیب داشتن دو ضلع مثلث قائم الزاویه، ضلع دیگر به سادگی محاسبه می شود.

2-11 نسبت طلایی

اگر طول دو ضلع قائمه مثلث قائم الزاویه، مضرب یکسانی از 3 و 4 باشند (مثلا 9 و 12)، طول وتر نیز همان مضرب از 5 خواهد بود (15).

اثبات

در نظر بگیرید که طول دو ضلع قائمه و وتر به صورت $3x,4x,5x$ باشد؛ مطابق رابطه (1) داریم:

$\Large (3x)^2+(4x)^2=(5x)^2 $

حال پرانتزها را به توان دو رسانده تا عبارت زیر بدست آید:

$\Large 9x^2+16x^2=25x^2 $

از $x^2$ فاکتور می گیریم:

$\Large (9+16)x^2=(25)x^2 $

به عبارتی رسیدیم که به ازای هرمقدار x صحیح است؛ پس نسبت طلایی همیشه کار می کند.

3-11 جمع بندی فصل

در این فصل با قضیه ساده اما بسیار پرتکرار و پرکاربرد فیثاغورث آشنا شدیم. همچنین نسبت طلایی نیز برای تولید سریع یک مثلث قائم الزاویه گزینه ای کارآمد است که مطرح شد. تمرین 1 این فصل، شما را برای درک مفهومی مهم آماده خواهد کرد.

*1- زاویه B را در شکل 11-2 در نظر بگیرید؛ فرض کنید نسبت طول ضلع روبه روی این زاویه به طول وتر را به شکل زیر تعریف کنیم:

(2)

$\Large \sin(B)= \frac{b}{a}$

همچنین نسبت طول ضلع مجاور (کنار) این زاویه به طول وتر را به شکل زیر تعریف کنیم:

(3)

$\Large \cos(B)= \frac{c}{a}$

حال ثابت کنید که رابطه زیر برقرار است:

(4)

$\Large \sin(B)^{2}+\cos(B)^{2}=1$

که در رابطه (2)، (3) و (4)، sin و cos را نسبت های مثلثاتی می نامند. همچنین sin را سینوس و cos را کسینوس می خوانیم.