در فصل 9 با مفاهیم پایه ای مربوط به مثلث نظیر زاویه و انواع مشهور آن آشنا شدیم. حال قصد داریم که محیط و مساحت مثلث را بشناسیم و آن را محاسبه نماییم. برای اینکار ابتدا لازم است با مفهومی به نام ارتفاع آشنا شویم.

1-10 ارتفاع

بنابه تعریف، هر ارتفاع مثلث، پاره خطی است که از یکی از راس های مثلث شروع شده و بر ضلع روبه روی خود یا امتداد ضلع عمود می شود. کوتاه ترین مسافتی که می توان از راس، به خط منطبق بر ضلع روبه رو پیمود؛ طول یا اندازه این پاره خط است. پس به این طول، فاصله نیز می گویند. بدین ترتیب هرمثلث سه ارتفاع دارد.

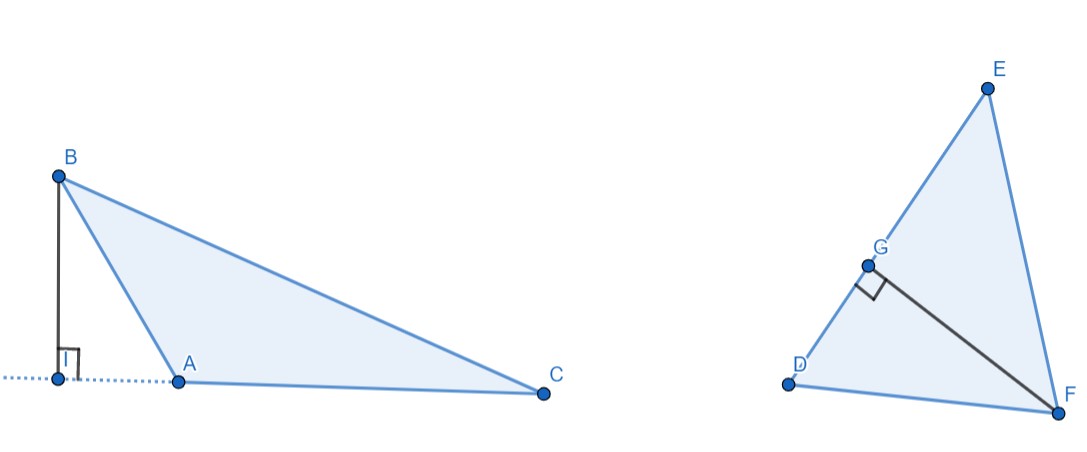
شکل 10-1، $FG$ و $BI$ هرکدام ارتفاع اند. توجه کنید که لزوما ارتفاع داخل مثلث نیست.

همانطور که در شکل 10-1 می بینید، ارتفاع مثلث، مثلث های قائم الزاویه می سازد.

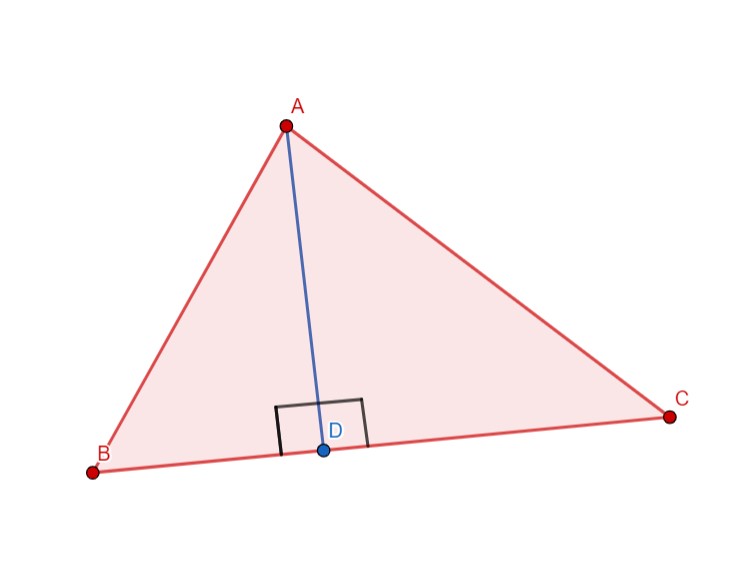
شکل 10-2، مثلث $ABC$ و یکی از ارتفاع های آن $AD$ که طول آن برابر با $h$ است.

2-10 محیط مثلث

محیط مثلث به سادگی مجموع سه ضلع مثلث است. در این فصل می خواهم آن را $2P$ بنامم؛ علتش را به زودی خواهید فهمید، ضمن اینکه در شکل 10-2، برای راحتی طول هرضلع را به حرف کوچک راس روبه روی آن می نامم، مثلا ضلع $BC$ را $a$ نام می گذارم:

(1)

$\Large 2P=a+b+c$

3-10 مساحت مثلث با داشتن ضلع و ارتفاع وارد بر ضلع

باز هم شکل 10-2 را درنظر بگیرید. به ضلع $BC$، ارتفاع $AD$ وارد می شود. از ضرب طول این دو و تقسیم بر 2، مساحث مثلث را به دست می دهد. البته خب این را هم درنظر بگیریم که این برای تمام ارتفاع ها و ضلع هایی که بر آن وارد می شوند صحیح است. پس با هر سه ارتفاع می توان این کار را انجام داد؛ طول ارتفاع وارد بر $AC$ را $h’$ و طول ارتفاع وارد بر $AB$ را $h^{”}$ در نظر بگیرید :

(2)

$\Large S=\frac{1}{2}ah=\frac{1}{2}bh’=\frac{1}{2}ch^{”}$

4-10 مساحت مثلث با داشتن طول سه ضلع (فرمول هرون)

بدون ارتفاع نیز می توان مساحت مثلث بدون نیاز به ارتفاع و صرفا با داشتن طول سه ضلع محاسبه نمود. محاسبه رابطه زیر برای اولین بار را به هرون اسکندرانی نسبت می دهند؛ توجه کنید که محیط را $2P$ در نظر گرفتیم پس $P$ نصف محیط است:

(3)

$\Large S=\sqrt{P(P-a)(P-b)(P-c)} $

* مثال 10-1)

بررسی کنید آیا مثلثی با اضلاع $2,5,7$ وجود دارد؟

پاسخ

از فرمول هرون (رابطه (3)) برای محاسبه مساحت چنین مثلثی بهره می بریم:

$\Large S=\sqrt{7(7-2)(7-5)(7-7)}=0

از نتیجه بالا، واضح است که چنین مثلثی وجود ندارد. این سوال ساده، ما را به نابرابری مثلثی رهنمون می سازد. برای اینکه مثلث تشکیل شود؛ طول هرضلع باید از مجموع طول دوضلع دیگر کوچکتر باشد. این را می توان از این پی برد که نصف محیط (برای مثبت بودن مساحت در فرمول هرون) باید از همه اضلاع بزرگتر باشد.

5-10 جمع بندی فصل

در این فصل با مفهوم ارتفاع، محیط و مساحت مثلث آشنا شدیم و همینطور دیدیم که رابطه زیبایی به نام فرمول هرون وجود دارد که با داشتن اضلاع مساحت مثلث را محاسبه می کند. مثلث در عین سادگی شکل بسیار مهمی است. برای حل مسائل هندسی گاهی وقت ها اشکال را به مثلث هایی تقسیم می کنیم و آن را حل می کنیم. به تمرین 2 این فصل نیز حتما بپردازید.

*1- شکل 10-2 را در نظر بگیرید؛ با استفاده از رابطه (2) و (3) اندازه هرسه ارتفاع مثلث را محاسبه نمایید. (برحسب اضلاع و نصف محیط)

*2- در مثلث دلخواهی، فرض کنید:

(4)

$\Large a^{2}+b^{2}=c^{2}$

با استفاده از روابط (3) و (4) نشان دهید در این مثلث خاص، مساحت از رابطه زیر قابل محاسبه است:

(5)

$\Large S=\frac{1}{2}ab$

رابطه (4)، قضیه فیثاغورث نام دارد؛ در فصل 9 گفتم که دو ضلع مثلث قائم الزاویه برهم عمودند؛ $a$ و $b$ همان دو ضلع اند و $c$ وتر مثلث است. مثلث قائم الزاویه حالتی خاص و جالب از مثلث است که دو ارتفاع از سه ارتفاع آن، خود اضلاع قائمه مثلث می باشد!