در فصل 4، خطوط و اشکال ، کمی در مورد مفاهیم بنیادی هندسه- به خصوص چندضلعی – گفتگو کردیم. حال می خواهیم به پایه ای ترین نوع چندضلعی( و شاید مهم ترین آن) بپردازیم. مثلث یک سه ضلعی است. فکر می کنم نیازی به توضیح نباشد که چرا یک ضلعی و دو ضلعی بسته وجود ندارد! در این مورد از شهودتان کمک بگیرید. مثلث ها ویژگی هایی دارند که براساس آن طبقه بندی می شوند؛ در این فصل می خواهیم با انواع مشهور مثلث آشنا شویم.

1-9 زاویه

زاویه یکی از آن ویژگی های مورد اشاره است. به طور عام، زاویه میزان بازشدگی یک خط از خط دیگر را نشان می دهد. مثلا اگر زاویه میان دو خط صفر باشد یعنی این دو خط برهم منطبق اند یا مفهوم مهم عمود بودن، زمانی اتفاق می افتد که خط به هر طرف باز شود؛ بازشدگی لازم برای انطباق با خط دیگر یکسان باشد. یکای زاویه درجه است. خط A که با خط B زاویه صفر دارد، اگر 180 درجه بازشود دوباره بر خط B منطبق شود. پس زاویه خط A با خط B در حالت عمود، 90 درجه است. درجه را با نماد ° نیز نمایش می دهند. زاویه های کوچکتر از 90 درجه را زاویه تند یا زاویه حاده می گویند. زاویه های 90 درجه، زاویه راست یا زاویه قائمه نامیده می شود و زوایای بزرگتر از 90 و کوچکتر از 180 را زاویه باز یا زاویه منفرجه می گویند و در آخر زاویه 180 درجه، زاویه نیم صفحه نام دارد.

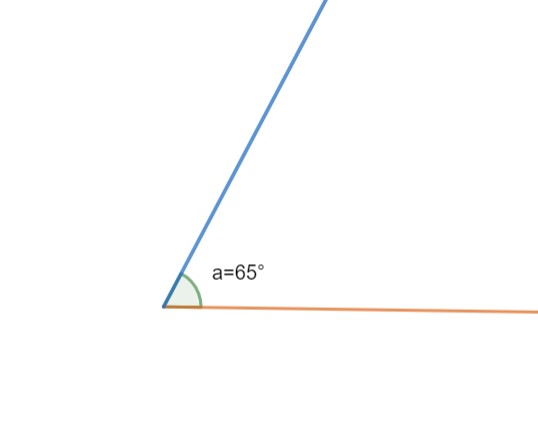
شکل 9-1، زاویه میان دو پاره خط 65 درجه است.

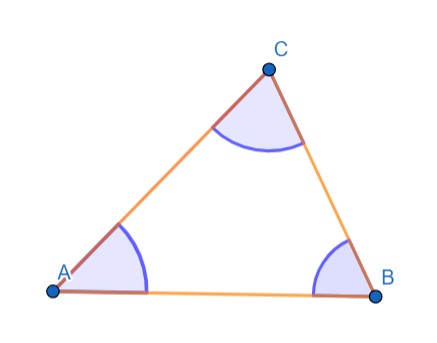
شکل 9-2، مثلث $ABC$ و سه زاویه آن

2-9 مجموع زوایای داخلی مثلث

مثلث شکل 9-2 را در نظر بگیرید؛ سه زاویه داخلی$A , B , C$ مثلث اگر در کنار هم قرار گیرند، تشکیل یک زاویه نیم صفحه می دهند پس مجموع زوایای داخلی مثلث به صورت زیر است:

(1)

$\Large A+B+C=180^{\circ}$

* مثال 9-1)

$x$ را در شکل 9-3 بیابید.

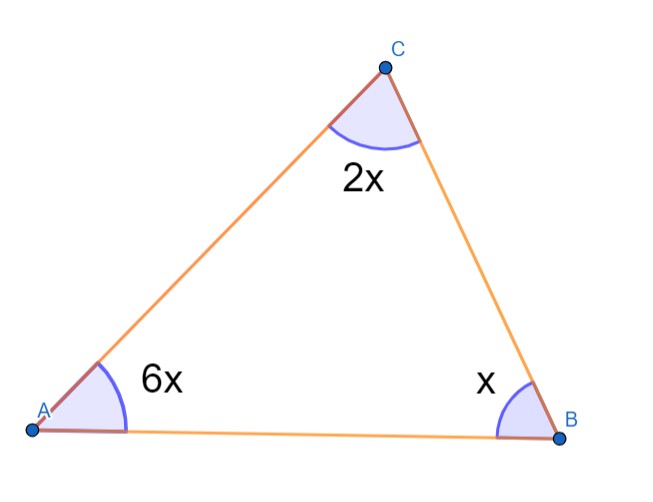
شکل 9-3، مثال 9-1

پاسخ

با استفاده از رابطه (1)، می دانیم که تنها باید یک معادله درجه اول حل کنیم:

$\Large 6x+x+2x=180 \rightarrow 9x=180 \rightarrow x=20^{\circ}$

پس از معرفی زاویه، دیگر تمامی ابزارهای لازم برای معرفی مختصر چند مثلث خاص را داریم:

3-9 مثلث متساوی الاضلاع

ساده ترین نوع مثلث، مثلثی است که هر سه ضلع آن برابر باشد. نکته جالب در مثلث تبعیت زوایا از اضلاع است یعنی در مثلث متساوی الاضلاع هر سه ضلع و هر سه زاویه باهم برابرند؛ پس فوری می توانید حدس بزنید که هر زاویه مثلث متساوی الاضلاع چند درجه است؛ آفرین، $60$ درجه.

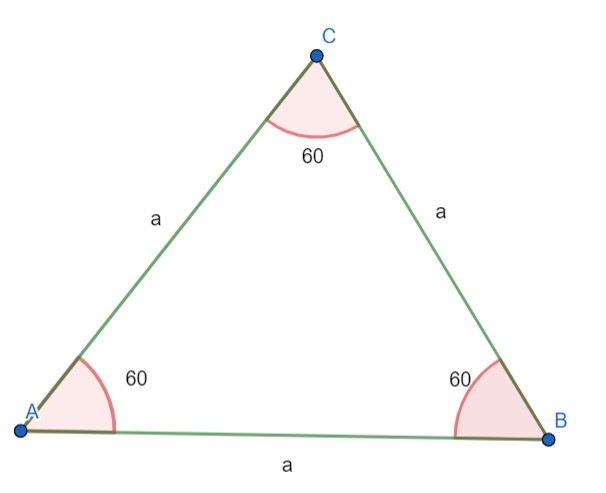
شکل 9-4، مثلث متساوی الاضلاع، با سه ضلع به اندازه a و سه زاویه 60 درجه

4-9 مثلث متساوی الساقین

دیگر نوع مثلث، مثلثی است که دو ضلع آن باهم برابر باشند که به هرکدام ساق مثلث می گوییم. بازهم به قاعده زیبای تبعیت زوایا از اضلاع، زاویه مابین هر ساق با ضلع سوم (ضلعی که اندازه آن با ساق ها برابر نیست) یکسان است. بدین ترتیب مثلث متساوی الاضلاع، مثلث متساوی الساقینی است که ضلع سوم نیز با ساق ها برابر است.

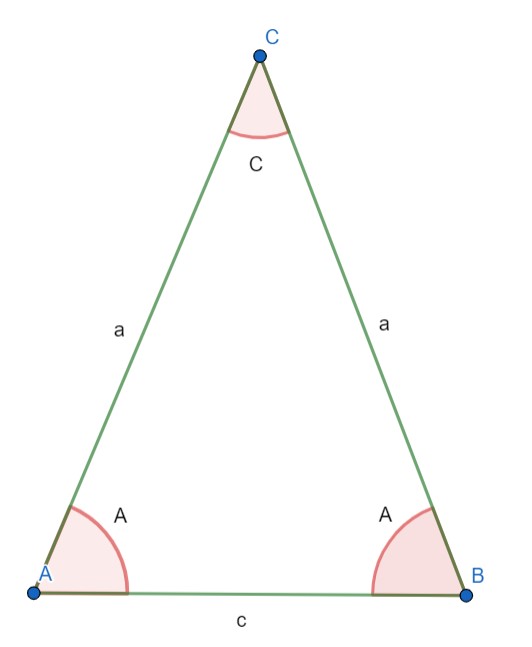
شکل 9-5، مثلث متساوی الساقین با ساق هایی به اندازه a و ضلع سوم به اندازه c؛ زاویه های پای ساق برابر با A و زاویه بین دو ساق برابر با C

5-9 مثلث قائم الزاویه

مثلثی که یکی از زاویه های آن قائمه یا 90 درجه باشد را مثلث قائم الزاویه می نامیم. در این مثلث، ضلع روبه رو به زاویه 90 درجه را وتر گوییم و دو ضلع دیگر را اضلاع قائمه می نامیم. اندازه وتر همیشه از اندازه هرکدام از اضلاع قائمه بزرگتر است ( همیشه ضلع روبه رو به بزرگترین زاویه، بزرگترین ضلع مثلث است. با توجه به رابطه (1)، در مثلث قائم الزاویه دو زاویه دیگر حتما از 90 درجه کوچک ترند) درحالت خاص مثلث قائم الزاویه می تواند متساوی الساقین نیز باشد اما متساوی الاضلاع خیر(به این توجه کنید که تمامی زاویه های مثلث متساوی الاضلاع 60 درجه است)

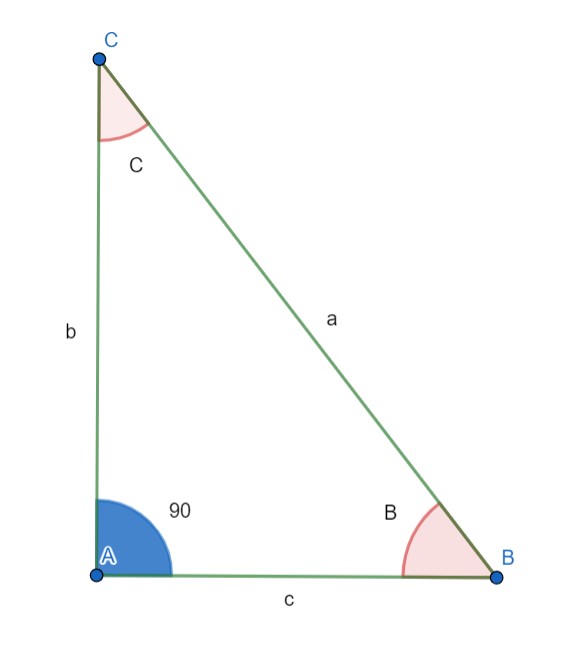
شکل 9-6، مثلث قائم الزاویه، زاویه قائمه با رنگ آبی مشخص است.

6-9 مثلث مختلف الاضلاع

مثلثی که هیچ دو ضلعی در آن باهم برابر نباشند را مختلف الاضلاع گوییم. در این نوع مثلث هیچ دو زاویه ای نیز با هم برابر نخواهند بود. مثلث قائم الزاویه در حالت کلی (به جز یک حالت خاص که در تمرین 1 به آن می پردازیم) یک مثلث مختلف الاضلاع است.

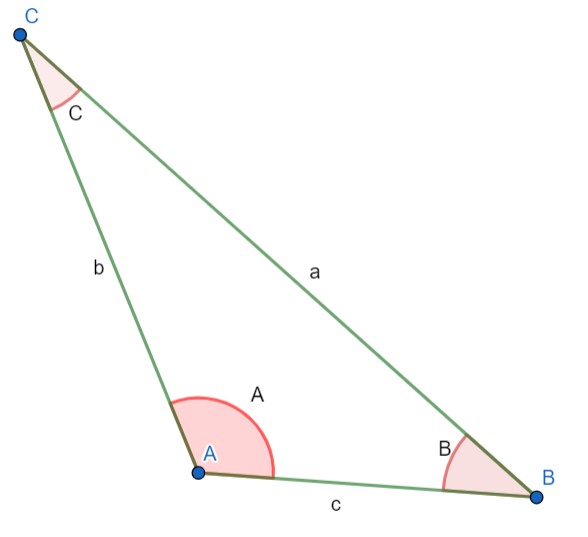
شکل 9-7، مثلث مختلف الاضلاع

7-9 جمع بندی فصل

این فصل تنها یک آشنایی مفید و مختصر با مثلث های خاص و مفهوم زاویه بود. به این ها بعدها بیشتر خواهیم پرداخت. این نکته را نیز در نظر بگیرید که در مسائلی که پای مفاهیم هندسی همچون مثلث به وسط می آید؛ کشیدن شکل یک الزام برای پیشبرد حل مسئله است. در مورد تصویرسازی رایانه ای نیز، حالت Geometry، وبسایت GeoGebra را پیشنهاد می کنم که نسخه آندروید آن نیز در گوگل پلی نیز موجود است.

*1- در بخش 9-5 و 9-6 صحبت هایی از یک حالت خاص که به آن مثلث قائم الزاویه متساوی الساقین می گوییم؛ به میان آمد. با در نظر گرفتن ویژگی های دو مثلث متساوی الساقین و قائم الزاویه، این مثلث را رسم کرده و مقدار سه زاویه آن را به دست آورید.