در این فصل می خواهیم با نحوه نمایش یک خط در دستگاه مختصات آشنا شویم. زود برویم سر اصل مطلب، یک معادله خط، تحول یک معادله درجه یک به ازای مقادیر مختلف را بررسی می کند. فقط این بار معادله درجه یک ما دارای دو مجهول است که چون این مجهول ها تنها یک جواب مشخص ندارند بلکه دسته ای نامتناهی از جواب ها برای این دو وجود دارد. به آن متغیر نیز می گوییم. البته هرگاه یک مقدار مشخص را برای یکی از متغیرها انتخاب کنیم؛ تنها یک جواب بدست می آید که خاصیت معادله درجه اول است.

1-8 تعریف

شکل کلی یک معادله خط را در ادامه خواهم آورد. فقط ابتدا باید ببینیم که کی به کی است! با توجه به اینکه قرار است روی دستگاه مختصات یک نمودار یا شکل ایجاد شود؛ باید اثری از هردو متغیر دستگاه یعنی $x$ و $y$ در رابطه مورد نظر باشد؛ شکل کلی که قولش را دادم در پایین آمده است:

(1)

$ \Large y=ax+b $

در رابطه (1) $x$ و $y$ متغیر هستند و $a$ و $b$ دو عدد معلوم و ثابت. نکته ای که در مقدمه این فصل در مورد ارتباط معادله درجه یک با معادله خط گفتم را با $y=c$ می توانید امتحان کنید.(c نیز یک عدد معلوم و ثابت است)

2-8 رسم نمودار

به رابطه (1) یکبار دیگر خوب توجه کنید؛ درصورتی که $x=0$ باشد؛ $y=b$ خواهد بود. پس نقطه برخورد خط با محور y، $(0,b)$ خواهد بود. به همین علت به b عرض از مبدا می گویند. طول از مبدا هم داریم؟داریم! اگر $y=0$ باشد آنگاه $x=\frac{-b}{a}$ خواهد بود که همان طول از مبدا دلخواه ماست؛ با اتصال این دو نقطه به هم و امتداد دادن خط، می توان خط مدنظر را رسم شده دانست. دیگر نام مهمی که لازم است بدانید شیب خط است فرض کنید $x_{0}$ ، $y_{0}$ و $x_{1}$ ، $y_{1}$ دو مقدار خاص اند که در رابطه (1) صدق می کنند. پس داریم:

(2)

$\Large y_{1}=ax_{1}+b$

$\Large y_{0}=ax_{0}+b$

پس اشکالی ندارد معادله بالایی را از معادله پایینی کم کرد:

(3)

$\Large y_{1}-y_{0}=a(x_{1}-x_{0})$

بدین ترتیب شیب به صورت زیر بدست می آید:

(4)

$\Large a=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}$

رابطه (2) و (4) این را به ما گوشزد می کند که با داشتن شیب و یک نقطه نیز می توان خط را به راحتی رسم نمود. مفهوم هندسی شیب در اصل این است که اگر یک خانه به سمت راست موازی با محور x جابجا شویم؛ چه مقدار موازی با محور y بالا یا پایین می رویم.

* مثال 8-1)

معادله خط $y=x-1$ را رسم کنید.

پاسخ

در اینجا می خواهم از روش دوم بهره ببرم. ابتدا یک نقطه بدست می آورم: نقطه C به صورت روبرو است:$C=(1,0)$ حال از مفهوم هندسی شیب بهره می برم تا نمودار را رسم کنم؛ $a=1$ نشان دهنده یک خانه به راست و یک خانه به جلوست$C’=(2,1)$؛ پس به راحتی نمودار رسم می شود:

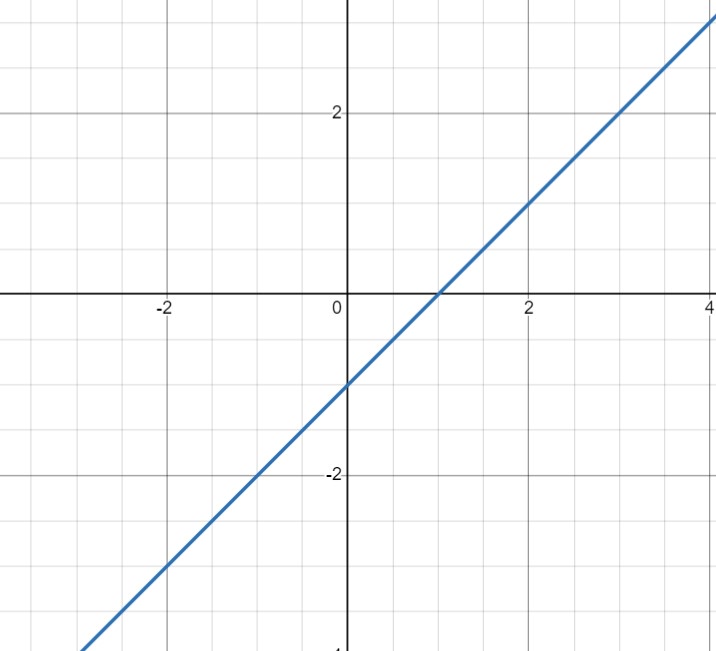
شکل 8-1، نمودار $y=x-1$

3-8 جمع بندی فصل

با فرم کلی معادله خط و نحوه رسم آن آشنا شدیم؛ اگر هرمعادله ای را دیدید که در آن توان y و x یک بود ولی کمی با فرم رابطه (1) تفاوت داشت؛ نگران نشوید. با عملیات های مناسب می توان هرمعادله خطی را به فرم (1) در آورد. مثلا اگر y دارای ضریبی بود؛ کل معادله را بر آن تقسیم کنید و سپس y را در یک طرف تساوی تنها کنید. تمرین 1 این فصل برای دستگرمی در همین موضوع است. برای رسم آنلاین و آشنایی با نمودارهای خطی می توان از بسته های نرم افزاری یا وبسایت های مختلفی بهره برد اما پیشنهاد من برای یک تجربه سریع، وبسایت دسموس است.

*1- معادله $\frac{y}{2}+\frac{x}{5}=3$ را ابتدا به فرم رابطه (1) درآورده و سپس رسم نمایید. توجه کنید که همه خط ها صعودی نیستند و شیب منفی هم ارز نمودار خطی نزولی است.

*2-یک خط با شیب بی نهایت یا شیب صفر به چه شکل خواهد بود؟ برای هردو مثالی بنویسید.