این فصل به بررسی جایگاه نقاط بر یک محور (یک بعدی) و یک صفحه(دو بعدی) می پردازم. مثل یک صفحه شطرنج 8×8 که می توان جایگاه هر خانه را بوسیله شماره خانه از چپ و شماره خانه از پایین مشخص کرد.

 

شکل 3-1، صفحه شطرنج

برای مثال در شکل بالا چهار فیل در مختصات (3,1)، (6,1)، (3,8) و (6,8) قرار دارند.

1-3 محور

محور خطی مدرج و بی نهایت است. از بی نهایت منفی ها می آید و به بی نهایت مثبت ها می رود. می توان به سادگی جمع و تفریق را به روی آن انجام داد که خب عملی ابتدایی است. برای مثال اگر در خانه 2 قرار داشته باشیم می توانیم 3 خانه جلو برویم تا به 5 برسیم یا 2 خانه عقب بیایم تا به 1 برسیم.

شکل 3-2، محور اعداد

 

2-3 مختصات

مختصات دوبعدی که در آن می توان جایگاه را بر یک صفحه مشخص نمود، از دو محور اعداد عمود بر هم ساخته می شود.

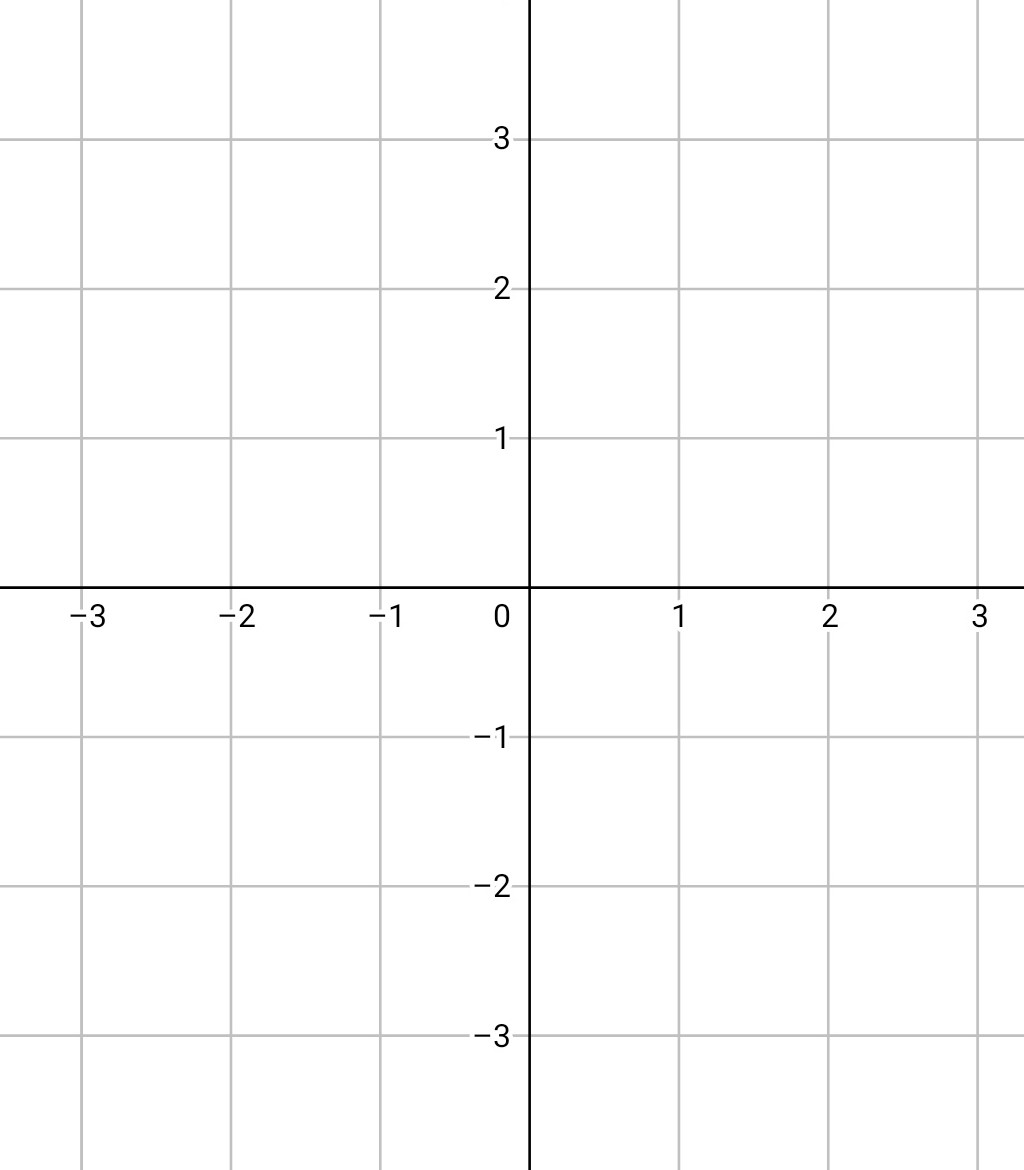
شکل 3-3، صفحه مختصات با دو محور

همانطور که در شکل 3-3 دیده می شود، محورهای مختصات صفحه را به چهار قسمت تقسیم می کنند. محور چپ به راست که در شکل 3-3 دیده می شود را محور طول ها یا محور x می نامیم. محور پایین به بالا را محور عرض ها یا محور y می نامیم. هر

 

نقطه در صفحه مختصات، دارای دو مشخصه یا دو تصویر بر هرکدام از محورهاست. می توان خطی را از نقطه فرضی به موازات محور y کشید، محل برخورد این خط با محور x، طول نقطه یا مشخصه x نقطه است. همچنین خطی به موازات محور x از نقطه فرضی، با محور y برخورد می کند که محل برخورد این خط با محور y، عرض نقطه یا مشخصه y نقطه است.

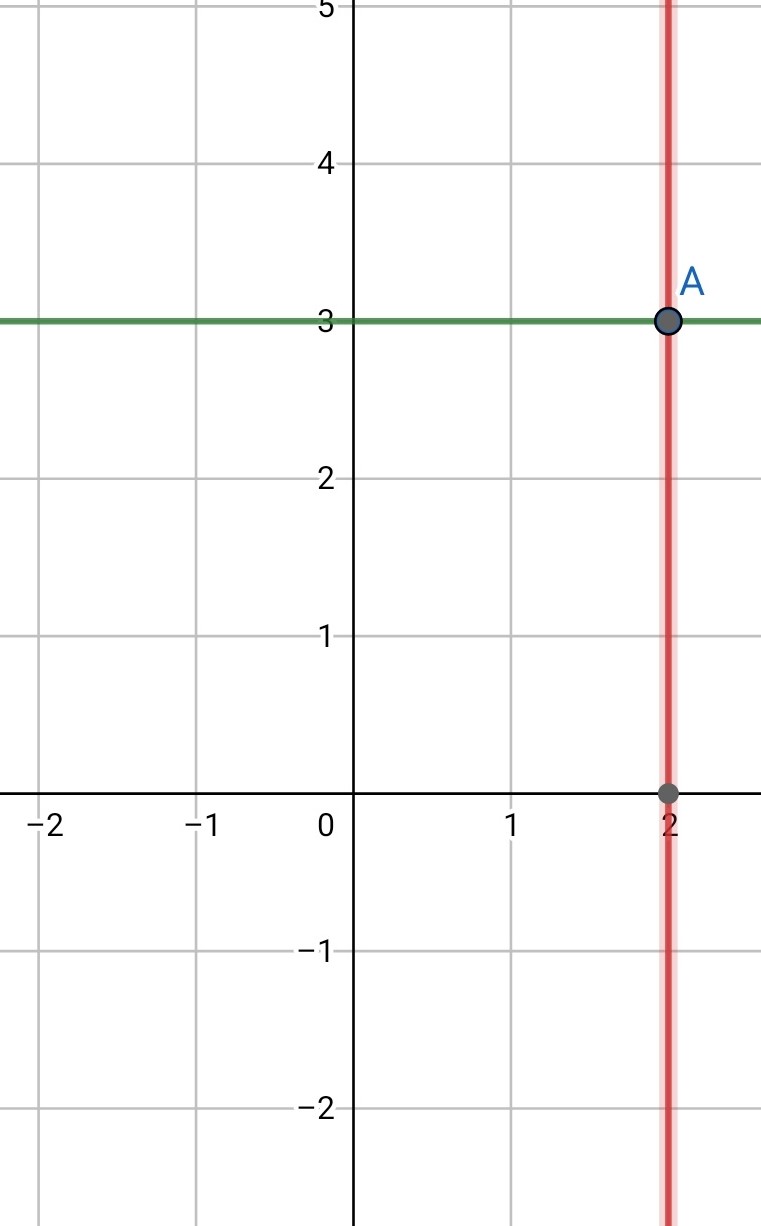
شکل 3-4، نقطه A که در آن x=2 است و y=3.

 

3-3 نقطه

در بخش قبل با مختصات نقطه آشنا شدیم. دو نمایش مرسوم برای توصیف یک نقطه در صفحه مختصات داریم که به صورت زیر است:

(1)

$\Large A=(x,y)$

$ \Large A=\begin{bmatrix}x \\ y \end{bmatrix} $

* مثال 3-1)

مختصات نقطه A در شکل 3-4 را مشخص شده، را نسبت به محور x ها قرینه کنید.

پاسخ

قرینه نسبت به محور x ها، مانند قرینه کردن مختصه y است.

(2)

$ \Large \begin{bmatrix}x
\\
y
\end{bmatrix} \rightarrow \begin{bmatrix}x
\\
-y
\end{bmatrix} $

پس جواب به صورت زیر است:

$ \Large  A’=\begin{bmatrix}2
\\
-3
\end{bmatrix} $

4-3 قرینه

حال که مثال بالا را آوردم خوب است که دو قرینه‌سازی مشهور دیگر را علاوه بر رابطه ای که در مثال دیدیم، تماشا کنیم:

 

قرینه نسبت به محور y ها:

(3)

$\Large \begin{bmatrix}x
\\
y
\end{bmatrix} \rightarrow \begin{bmatrix}-x
\\
y
\end{bmatrix} $

قرینه نسبت به مبدا مختصات:

(4)

$ \Large \begin{bmatrix}x
\\
y
\end{bmatrix} \rightarrow \begin{bmatrix}-x
\\
-y
\end{bmatrix} $

 

در کل می توان گفت هرگاه نسبت به چیزی درحال قرینه‌سازی هستیم، از نقطه مبدا، به اندازه فاصله خود به سمت نقطه تقارن می رویم سپس به اندازه همان فاصله و در همان جهت از نقطه تقارن دور می شویم تا به نقطه مقصد برسیم.

* مثال 3-2)

مطابق شکل 3-5، قرینه نقطه A نسبت به نقطه Β را بیابید.

 

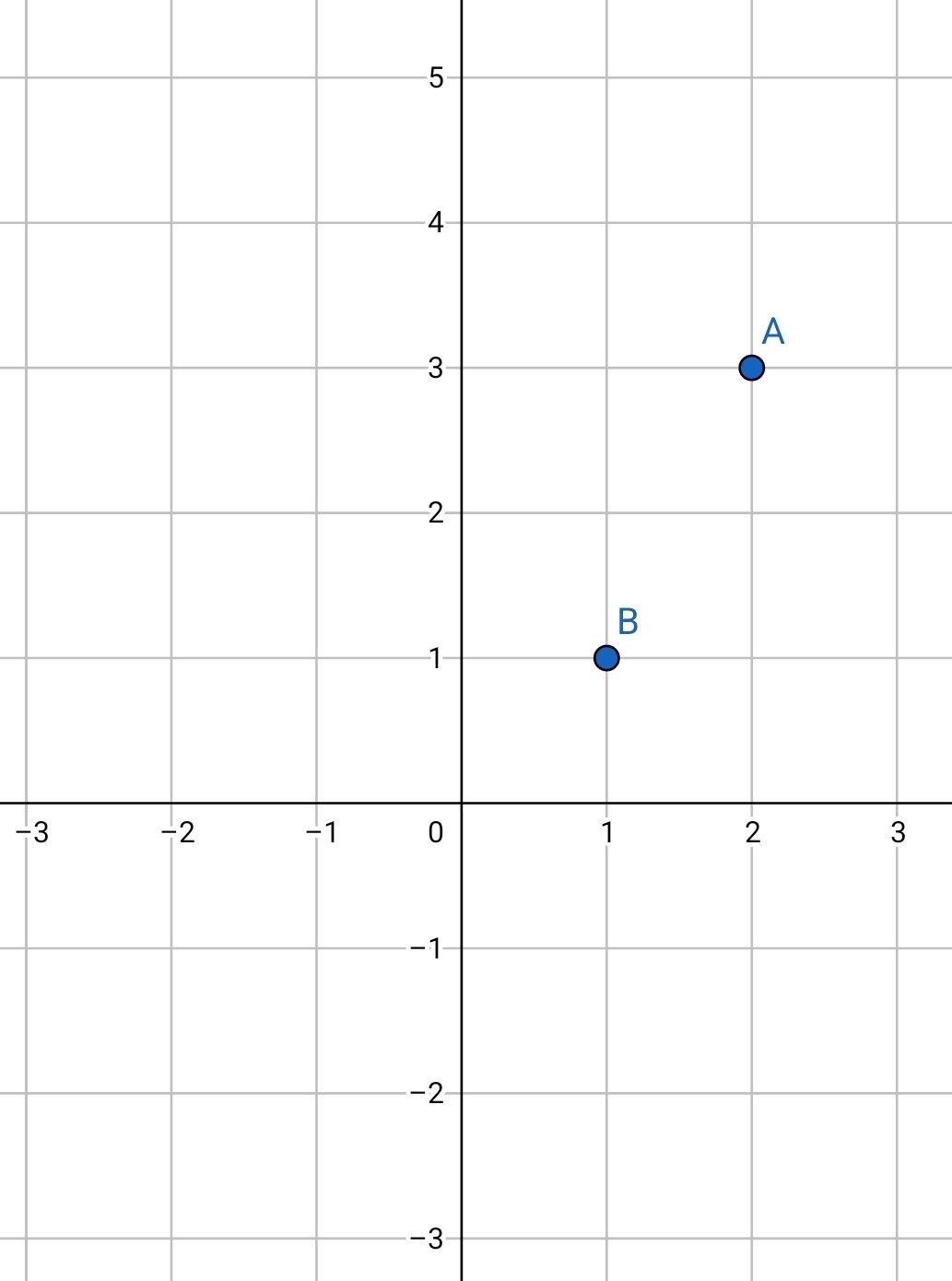
شکل 3-5، شکل مثال 3-2

پاسخ

ابتدا نقطه A را روی محور x قرینه می کنیم، از آنجا که تصویر دو نقطه 1 واحد فاصله دارند؛ 2 واحد به سمت چپ حرکت می کنیم تا مشخصه x نقطه قرینه بدست آید (x=0). سپس روی محور y، 4 واحد به پایین حرکت می کنیم.(y=-1) بدین ترتیب مختصات نقطه قرینه بدست آمد.

 

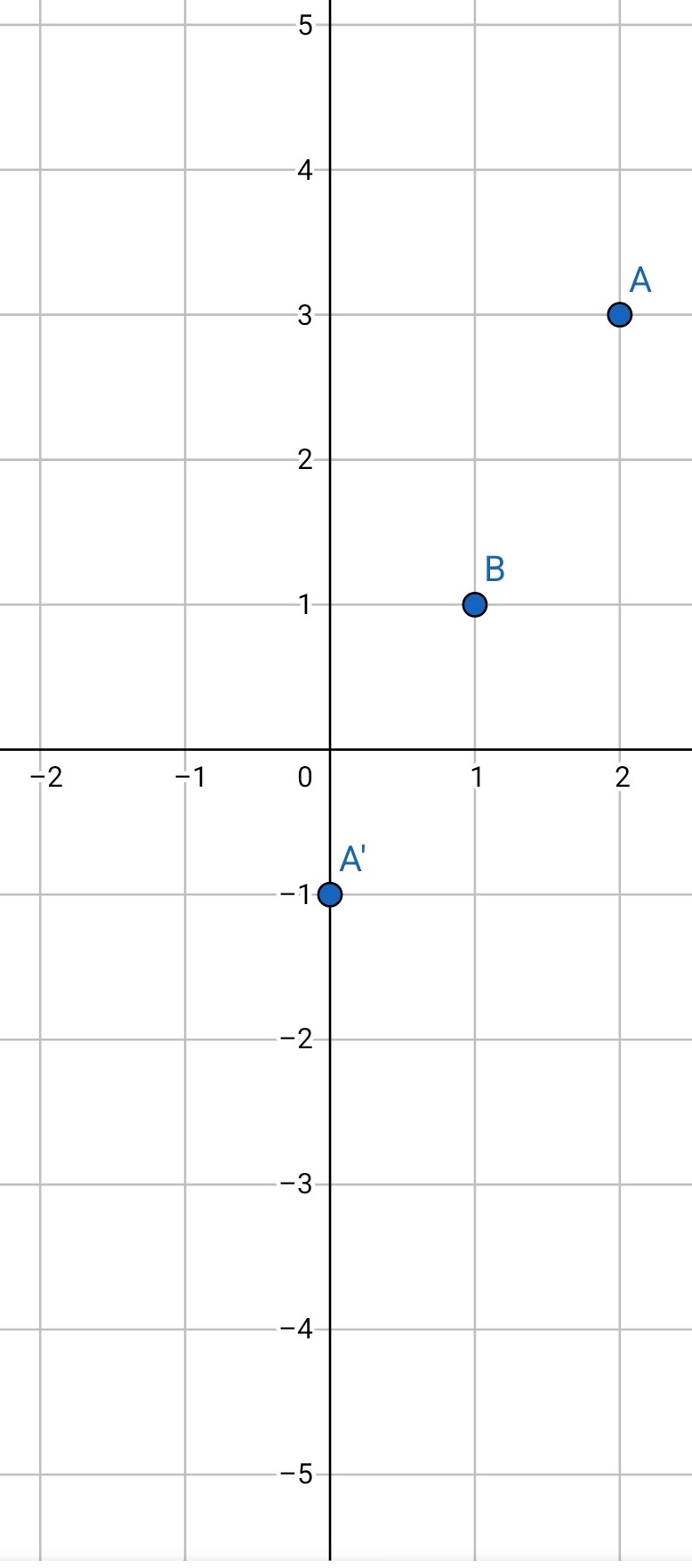
شکل 3-6، پاسخ مثال 3-2

 

5-3 جمع بندی فصل

در این فصل با مفهوم نقطه و مختصات آن و محور های مختصات به طور ابتدایی آشنا شدیم. عمدتا ابداع این دستگاه مختصات را به دانشمند و فیلسوف شهیر، رنه دکارت (René Descartes) نسبت می دهند. از این رو به این دستگاه مختصات، دستگاه مختصات دکارتی نیز گفته می شود.

 

رنه دکارت 1650-1596

 

ترتیب فصل	قبلی	فعلی	بعدی
عنوان	2 کسر و توان	3 مختصات	4 خطوط و اشکال