در این فصل می خواهیم نگاهی به دو معادله دو مجهول بیندازیم؛ البته معادلات ما فراتر از یک معادله خط نخواهد رفت. مشخص است که یک معادله و دو مجهول دارای بی شمار جواب است. پس نیاز داریم که به تعداد مجهول ها معادله داشته باشیم تا برای هر مجهول مقداری یکتا بدست بیاید.

1-14 روش حل

یک دو معادله دو مجهول در حالت کلی به صورت زیر است:

(1)

$\displaylines{\left\{\begin{matrix} ax+by=e \\ cx+dy=f \end{matrix}\right.}$

که در آن تنها $x$ و $y$ مجهول اند. روش حل این است که در معادله اول، یکی از مجهول ها را (مثلا $y$) را برحسب $x$ بدست آورده و سپس در معادله دوم جایگذاری می کنیم. حال تنها یک معادله و یک مجهول داریم؛ آن را بدست آورده و سپس مجهول حذف شده را حساب می کنیم.

این همان مرحله اول کارمان است؛ محاسبه یکی از مجهول ها برحسب دیگری، برای اینکار از معادله اول بهره بردم:

(2)

$\Large y=\frac{e}{b}-\frac{a}{b}x$

حال عبارت سمت راست تساوی بالا را به جای $y$ در معادله دوم می گذارم:

$cx+d\frac{e}{b}-d\frac{a}{b}x=f$

باید این معادله درجه اول را حل کرد تا به x برسیم:

$ً\frac{cb-da}{b}x=f-\frac{de}{b}$

با تنها کردن $x$ به عبارت زیر می رسیم:

(3)

$\Large x=\frac{fb-de}{cb-da}$

بخاطر سپردن این رابطه خیلی سودمند نیست چون محاسبه آن بسیار آسان بود ولی خوب بود که نحوه محاسبه را دیدید. به این ترتیب $x$ معلوم است و می توان از هرکدام از معادله های رابطه (1) یا (2) $y$ را حساب کرد.

(4)

$y=\frac{e}{b}-\frac{a}{b}(\frac{fb-de}{cb-da})$

* مثال 14-1)

دستگاه دو معادله ای روبه رو را حل کنید.

$\displaylines{\left\{\begin{matrix} 2x-y=3 \\ 4x+5y=-1 \end{matrix}\right.}$

پاسخ

روشی که مورد بحث قرار گرفت برای حل دستگاه معادلات کارساز است؛ اما اینجا می توانیم معادله را به شکلی ساده تر حل کنیم؛ کافی است معادله اول را در 5 ضرب کرده و سپس دو معادله را باهم جمع کنیم:

$\displaylines{\left\{\begin{matrix} 10x-5y=15 \\ 4x+5y=-1 \end{matrix}\right.}$

خواهیم دید که عوامل $y$ دار حذف می شوند:

$14x=14 \rightarrow x=1 \rightarrow y=-1 $

2-14 جمع بندی فصل

در این فصل با دو روش کلی حل دستگاه معادلات آشنا شدیم. این دستگاه را می توان به روش هندسی نیز حل کرد، می توان دو معادله خط داده شده را رسم نمود و نقطه برخورد این دو را حاصل در نظر گرفت اما در شرایطی که تنها با دو معادله خط سروکار داریم؛ شاید دو روش بالا (جایگذاری یکی از مجهول ها یا حذف یکی از آنها ) ساده تر از ترسیم باشد.

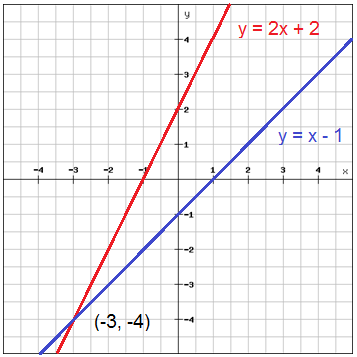
شکل 14-1، حل هندسی دستگاه معادلات

*1- آیا شرایطی وجود دارد که دستگاه معادلات، دارای جواب نباشد؟ (راهنمایی: به رابطه (3) نگاه کنید)

*2- دستگاه دومعادله دو مجهول زیر را حل کنید.

$\displaylines{\left\{\begin{matrix} 3x+6y=15 \\ x-4y=-1 \end{matrix}\right.}$