در این فصل به تابع نمایی می پردازیم. این تابع کاربرد فراوانی در علوم مختلف دارد. برای مثال تخمین سن فسیل ها، پیش بینی جمعیت یک جامعه انسانی یا حیوانی و همه گیری بیماری های واگیردار، با استفاده از توابع نمایی مدل می شوند. همانطور که از اسم تابع پیداست؛ تابع به توان(نما) مربوط است.

1-33 تعریف

در نظر بگیرید که $x$ متغیر مستقل است؛ تابع زیر را نمایی به پایه $a$ ($a$ عددی ثابت است) می خوانیم:

(1)

$\large f(x)=a^{x}$

البته به این شرط که $a$ مثبت باشد و یک نباشد:

(2)

$\large a>0,a\neq 1$

در صورتی که  $a=1$ باشد؛ $f(x)=1$ خواهد بود که یک تابع ثابت است نه نمایی. از نظر رفتار، توابع نمایی را به دو دسته تقسیم می کنیم؛ توابع نمایی با پایه بین صفر و یک $0<a<1$ و توابع نمایی با پایه بزرگتر از یک $1<a$.

2-33 توابع نمایی با پایه بین صفر و یک

دامنه تابع را مجموعه اعداد حقیقی در نظر بگیرید. در چنین شرایطی، هرچقدر $x$ بزرگتر شود، تابع کوچکتر شده و به صفر نزدیکتر می شود درحالیکه با کاهش مقدار $x$، مقدار تابع بزرگتر شده و کرانی ندارد. شکل 33-1 نمودار تابع $f(x)=(\frac{1}{2})^{x}$ را به ما نشان می دهد.

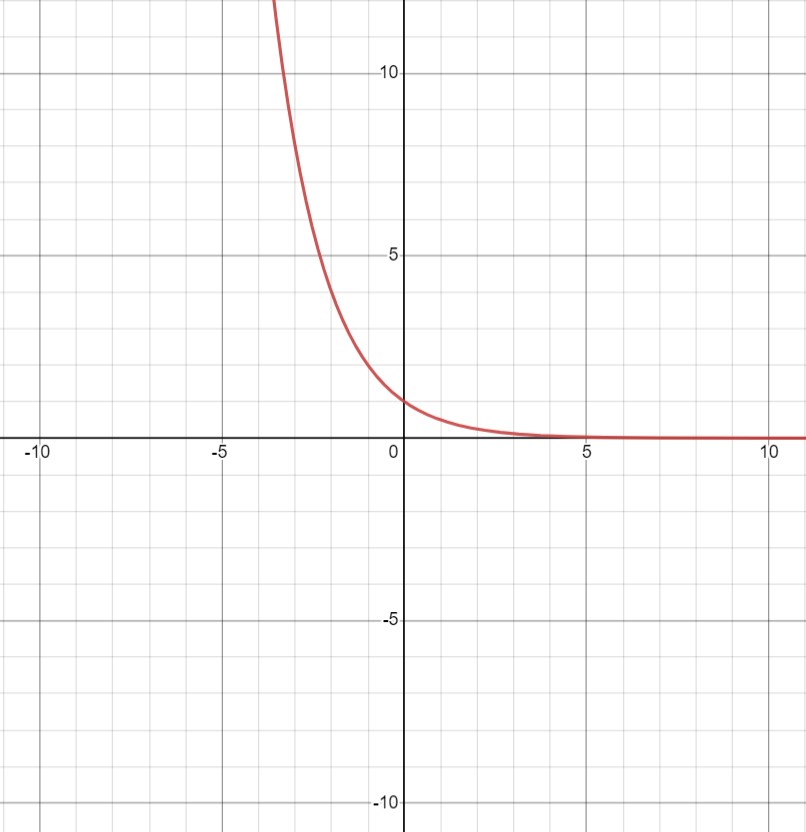
شکل 33-1، با افزایش مقدار $x$، تابع همیشه درحال نزدیک شدن به صفر است اما هیچ وقت به آن نمی رسد (برد تابع نمایی همواره اعداد حقیقی مثبت است.)

3-33 توابع نمایی با پایه بزرگتر از یک

رفتار این توابع کاملا برعکس توابع نمایی با پایه بین صفر و یک است. در اینجا با افزایش مقدار $x$، مقدار تابع همینطور بزرگتر می شود و کرانی ندارد؛ درحالیکه با کاهش مقدار $x$، تابع به صفر نزدیک و نزدیک تر می شود. شکل 33-2، بیانگر $f(x)=2^{x}$ است.

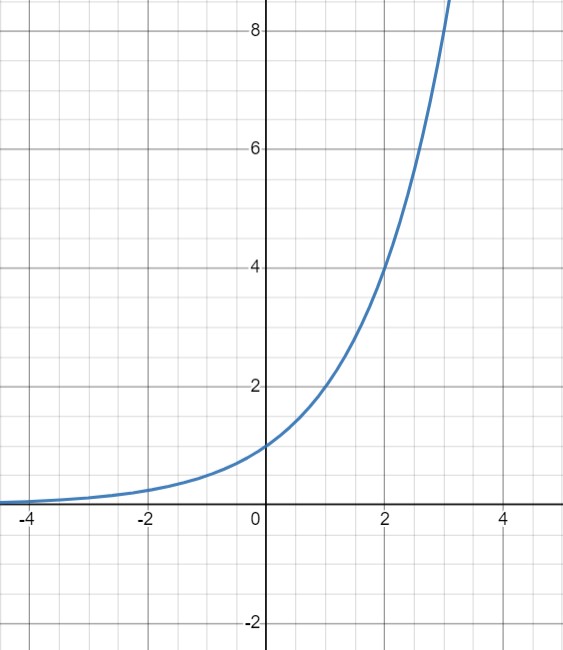
شکل 33-2، با افزایش مقدار $x$ تابع بزرگ و بزرگتر می شود. برد همواره اعداد مثبت حقیقی است.

4-33 تابع نمایی طبیعی

در ریاضیات، همانند عدد گنگ $\pi$، عدد گنگ مشهور و پرکاربرد دیگری به نام عدد اویلر داریم که با نماد $e$ نمایش داده می شود. مقدار تقریبی این عدد به صورت زیر است:

(3)

$\large e \approx 2.71828182846$

به تابعی نمایی که پایه آن عدد اویلر باشد؛ تابع نمایی طبیعی می گوییم. آن را با دو نماد $e^{x}$ یا $\exp(x)$ نمایش می دهیم. رفتار تابع نمایی طبیعی شبیه به بخش 33-3 است؛ زیرا عدد اویلر هم عددی بزرگتر از یک است اما دلیل تمایز این عدد و این تابع و همچنین حمل صفت طبیعی، حضور این تابع در پدیده های مختلف جهان علم است. انگار که در طبیعت این تابع وجود دارد!

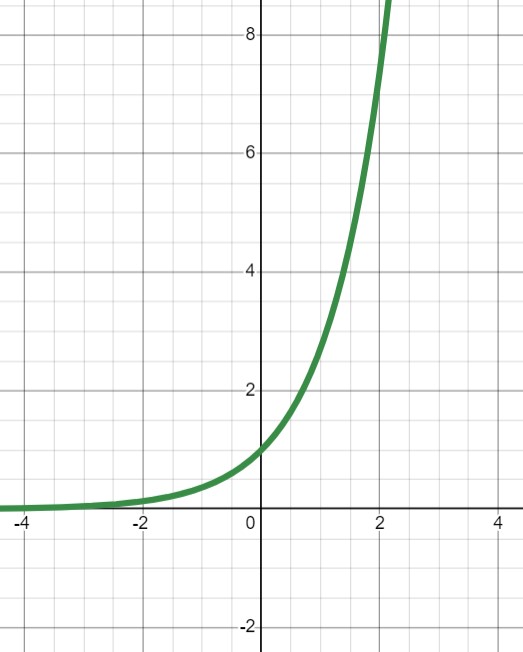
شکل 33-3، تابع نمایی طبیعی

5-33 جمع بندی فصل

این فصل را به تابع نمایی طبیعی پرداختیم. با کمی دقت می توان پی برد که توابع نمایی تاحدودی شبیه به دنباله های هندسی هستند و پایه همانند قدرنسبت عمل می کند؛ درست است اما تابع نمایی تنها اعداد طبیعی را به عنوان ورودی دربر نمی گیرد. میان تابع و دنباله این تفاوت وجود دارد. برای ساخت تصاویر نمودار ها از نرم افزار دسموس بهره بردم.

*1- جمعیت گونه ای گرگ در یک منطقه حفاظت شده، با تابع زیر داده می شود:

$\large f(x)=0.003\times e^{x-2012}$

که در آن $x$ نمایانگر سال میلادی است؛ در سال $2022$ تقریبا چند قلاده گرگ در این منطقه زندگی می کند؟