
مثلثات ؛ جمع و تفریق زوایا و نسبت های مثلثاتی
در این مقاله به رابطه های مثلثاتی جمع و تفریق زوایا در توابع مثلثاتی می پردازیم. از مشهور ترین و پرکاربردترین روابط مثلثاتی، رابطه توابع

در این مقاله به رابطه های مثلثاتی جمع و تفریق زوایا در توابع مثلثاتی می پردازیم. از مشهور ترین و پرکاربردترین روابط مثلثاتی، رابطه توابع

در مقالات قبل، با توابع مثلثاتی و دایره مثلثاتی آشنا شدیم. اتحادهای مثلثاتی به ما در بدست آوردن مقادیر مثلثاتی با استفاده از ترکیب توابع

در مقاله قبلی با توابع مثلثاتی آشنا شدیم؛ در این مقاله با مفهوم دایره مثلثاتی و کاربرد های آن آشنا می شویم. دایره مثلثاتی یا

مثلثات شاخه ای ریاضی است که روابط ما بین زوایا و اضلاع مثلث را بررسی می کند. بسیاری از علوم از جمله فیزیک به مثلثات
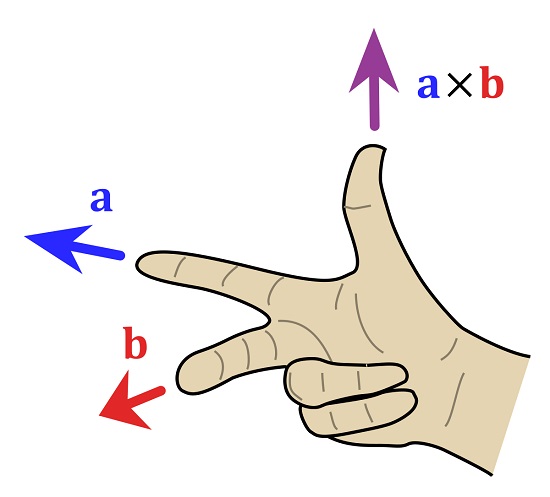
از آنجایی که کمیت های نرده ای و برداری زیادی با این موضوع سروکار دارندضرب برداری از مهم ترین دانستنی ها برای یادگیری علم فیزیک

مؤلفه های بردار، تصویر بردار روی هر محور هستند. برای ترسیم مؤلفه های بردار کافی است از دم بردار به موازات سر بردار روی محور

اهمیت بردار از این منظر است که در فیزیک و مهندسی با کمیت های زیادی سروکار داریم که علاوه بر اندازه دارای جهت نیز هستند.

اگر دو شکل را به توان با جابجایی یا چرخش یا بازتاب دادن بر هم منطبق نمود؛ آن دو را همنهشت می گوییم. بررسی همنهشتی

زاویه خارجی در یک چند ضلعی محدب، زاویه ای که بین ضلع و امتداد ضلعی دیگر ایجاد شود را زاویه خارجی می نامیم. زاویه خارجی