مثلثات ؛ دایره مثلثاتی

آموزش, آموزش ریاضی, آموزش هندسه

در مقاله قبلی با توابع مثلثاتی آشنا شدیم؛ در این مقاله با مفهوم دایره مثلثاتی و کاربرد های آن آشنا می شویم. دایره مثلثاتی یا واحد، دایره ای است با شعاع یک که محور x آن محور کسینوس ها و محور y آن محور سینوس هاست. همانطور که می دانیم مقداری بیش از 1 و کمتر از 1- برای سینوس و کسینوس امکان پذیر نیست که این در دایره مثلثاتی نیز لحاظ شده است:

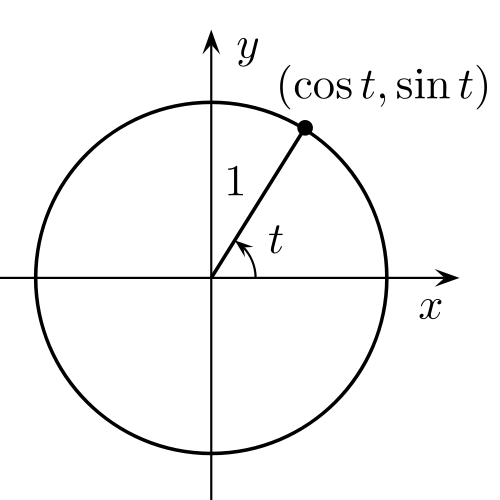
همانطور که در شکل بالا می بینیم تصویر شعاع مشخص کننده زاویه t بر روی محور x ها برابر با cos t و روی محور y ها sin t است که رابطه فیثاغورث بین شعاع و تصویر شعاع زاویه بر دو محور برقرار است:
(1)

$\sin^2 t+\cos^2 t=1$

همانطور که می بینیم در هر زاویه 90 درجه یا π/2 رادیان، زاویه یک ربع از دایره می پیماید. با توجه به 360 درجه بودن دایره، این دایره دارای چهار ربع است. دیگر کاربرد دایره مثلثاتی تعیین علامت سینوس، کسینوس و دیگر توابع مثلثاتی در یک زاویه خاص است.

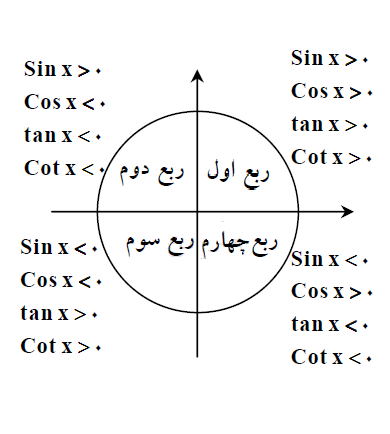ربع های دایره مثلثاتی و علامت توابع مثلثاتی در هر کدام از آنها؛ معمولا با کلمه هستک (ه: همه در ربع اول مثبت ، س: سینوس در ربع دوم مثبت ت: تانژانت در ربع سوم مثبت ک: کسینوس در ربع چهارم مثبت ) به خاطر سپرده می شود.

زاویه هر ربع به صورت زیر است؛ k می تواند هر مقدار صحیحی را شامل شود:

ربع اول $0+2k\pi < t < \frac{\pi }{2}+2k\pi \; \; \; \; k\in \mathbb{Z}$

ربع دوم

$\frac{\pi }{2}+2k\pi < t < \pi +2k\pi \; \; \; \; k\in \mathbb{Z}$

ربع سوم

$\pi +2k\pi < t < \frac{3\pi}{2} +2k\pi \; \; \; \; k\in \mathbb{Z}$

ربع چهارم

$\frac{3\pi}{2} +2k\pi < t < 2\pi+2k\pi \; \; \; \; k\in \mathbb{Z}$

*تمرین حل شده)

توابع مثلثاتی زاویه 47π/6 را تعیین علامت کنید.

برای تعیین علامت این توابع باید ابتدا مشخص زاویه در چه ربعی از دایره قرار می گیرد پس باید بزرگترین مضرب زوج ممکن π را از زاویه استخراج کنیم و مقدار باقی مانده را تعیین مکان کنیم.

$\frac{47\pi }{6}=\frac{11\pi}{6}+6\pi$

با توجه به اینکه 11π/6 ما بین 3π/2 و 2π قرار دارد؛ زاویه مدنظر ما در ربع چهارم واقع شده. با توجه به دایره مثلثاتی، سینوس منفی، کسینوس مثبت و حاصل تقسیم آنها تانژانت منفی خواهد بود.

تبدیلات سینوس زاویه

برای ما کار با زوایایی که ما بین 0 و π/2 هستند ساده تر است پس خوب است زاویه ای را ما بین این دو زاویه درنظر بگیریم و فرمول های کلی بر اساس سینوس آن زاویه در سه ربع دیگر پیدا کنیم.

(2)

$\sin t=\sin (\pi -t)=-\sin (\pi +t)=-\sin (2\pi -t)$

*تمرین حل شده)

(sin(π/6 برابر با 0.5 است؛ (sin(7π/6 را بیابید.

از بخش سوم تساوی 2 که مربوط به ربع سوم است استفاده می کنیم؛ سینوس زاویه مدنظر برابر 0.5- است.

تبدیلات کسینوس زاویه

به مانند سینوس، روابط تبدیلی مابین کسینوس نیز برقرار است. البته با اینکه t ابتدا برای مابین 0 و 2/π تعریف شد، اما می توان این تبدیلات سینوس و کسینوس را برای هر زاویه ای استفاده کرد.

(3)

$\cos t=-\cos (\pi -t)=-\cos (\pi +t)=\cos (2\pi -t)$

تبدیلات تانژانت زاویه

با تقسیم رابطه 2 و رابطه 3 بر هم تبدیلات زاویه تانژانت نیز بدست می آید:

(4)

$\tan t=-\tan (\pi -t)=\tan (\pi +t)=-\tan (2\pi -t)$

تصاویری از مقدار سینوس و کسینوس زوایای مهم

2 پاسخ

عرشیا گفت:

می 19, 2022 در 10:18 ق.ظ

ربع ها را اشتباه نوشتید

پاسخ
1. admin گفت:
  
  می 19, 2022 در 12:41 ب.ظ
  
  تصویر اصلاح شد. ممنون که همراه ما هستید.
  
  پاسخ

SCIENCIO

مثلثات ؛ دایره مثلثاتی

2 پاسخ

دیدگاهتان را بنویسید لغو پاسخ