61 خط در فضای سه بعدی
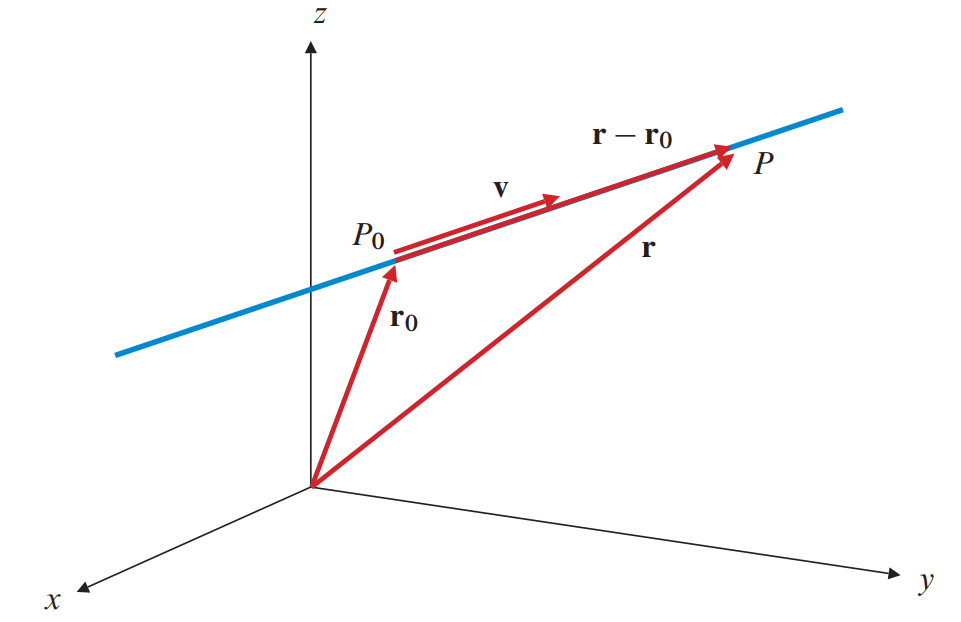
از کنار هم قرار گرفتن نقاط در فضای $\mathbb{R}^3$ ، خط تشکیل می شود. همانطور که در فصل قبل دیدیم؛ محل برخورد دو صفحه غیرموازی با یکدیگر، یک خط است. بردار موازی با این خط را می توان از ضرب خارجی بردارهای نرمال دو صفحه بدست آورد. در این فصل به خط و معادله آن […]
60 صفحه در فضای سه بعدی
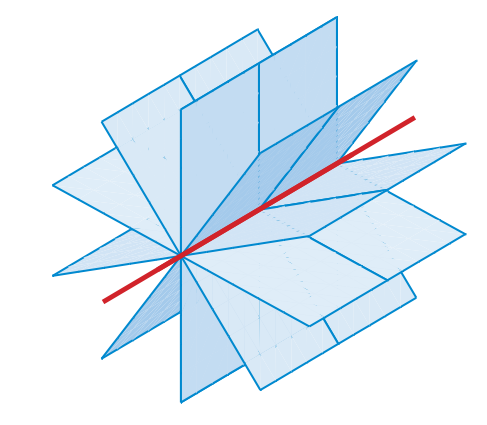
صفحه شکلی دوبعدی است که می خواهیم آن را در فضای سه بعدی بررسی کنیم و معادله صفحه را بدست آوریم. نقطه $P=(x,y,z)$ را در نظر بگیرید. یک معادله با سه متغیر $x$،$y$ و $z$ قیدی بر روی نقطه می گذارد که آزادانه نمی تواند در هرجای فضای سه بعدی قرار بگیرد. برای مثال معادله […]
59 بردار : ضرب خارجی
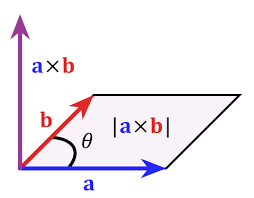
در فصل قبل با ضرب داخلی آشنا شدیم. ضرب خارجی عملی است که دو بردار سه مولفه ای را به عنوان ورودی می گیرد و یک بردار، عمود برهردو بردار ورودی را خروجی می دهد. ضرب خارجی در فیزیک الکترومغناطیس کاربرد بسزایی دارد. 1-59 تعریف دو بردار دلخواه$\vec{a}=\begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix}$ و $\vec{b}=\begin{bmatrix} […]
58 بردار : ضرب داخلی
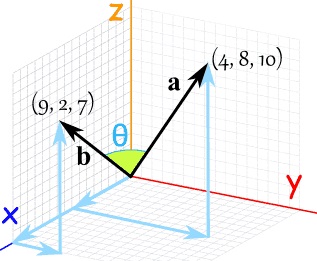
ضرب داخلی (ضرب نقطه ای یا ضرب اسکالر نیز گفته می شود)، عملی است که دو بردار را به عنوان ورودی می گیرد و یک عدد خروجی می دهد. برای آشنایی شکل کلی این ضرب، ابتدا خوب است کمی با بردارهایی با تعداد مولفه های بیشتر از دو آشنا شویم. 1-58 فضای سه بعدی برداری […]
57 بردار : مقدمه
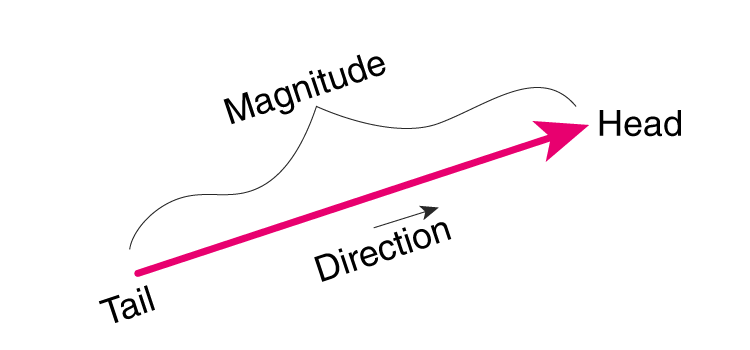
در علوم تجربی، گاها با کمیت هایی روبه‌رو می شویم که تنها دارای مقدار هستند. به این کمیت ها، کمیت اسکالر یا نرده ای می گوییم. کمیت های فیزیکی مانند جرم و دما اینگونه اند. اما کمیت هایی نیز وجود دارند که علاوه بر مقدار دارای جهت اند؛ مثلا در جابجایی یک جعبه بر روی […]
17 اتحادهای مثلثاتی: جمع دو زاویه
در فصل 15، با اتحادهای مثلثاتی که نتیجه قضیه فیثاغورث بودند؛ آشنا شدیم. این بار می خواهم با نوعی دیگر از اتحادهای مثلثاتی آشنا شویم. اتحادهایی که بیانگر جمع دو زاویه در آرگومان نسبت های مثلثاتی است. مثلا با دانستن نسبت های مثلثاتی زوایای $a$ و $b$ می توان نسبت های مثلثاتی زاویه $a+b$ را […]
16 رادیان
در این فصل، قصد داریم تا با یکایی دیگر برای معرفی زاویه آشنا شویم. همانطور که می دانید، درجه مشهورترین یکایی است که برای مقداردهی به زوایا می شناسیم. درجه، به طور قراردادی، $\frac{1}{360}$ زاویه ای است که یک دایره را به طور کامل دور می زند. حال در اینجا قصد دارم یکایی دیگر، شبیه […]
15 اتحادهای مثلثاتی: روابط فیثاغورثی
در فصل 12، نسبت های مثلثاتی را شناختیم. در مثلثات هم اتحادهایی داریم که در محاسبات مختلف، یاور ما خواهند بود و میان نسبت های مثلثاتی، پل هایی کاربردی ایجاد می کنند. اتحاد های مثلثاتی گاهی به سادگی و گاهی به دشواری اثبات می شوند اما نکته مهم به خاطر سپردن برخی از آنها است. […]
12 نسبت های مثلثاتی
در تمرین 11-1، گریزی به مفهوم نسبت های مثلثاتی زدیم. در این مقاله قصد معرفی تمامی نسبت های مثلثاتی را دارم. نسبت های مثلثاتی، حاصل تقسیم طول یکی از اضلاع مثلث قائم الزاویه به دیگر ضلع است؛ از آن جایی که 3 ضلع داریم، این انتظار را داریم که 6 نسبت مثلثاتی داشته باشیم. مشهور […]
11 قضیه فیثاغورث
در فصل 10، تمرین 2 گریزی به قضیه فیثاغورث زدیم. بنظرم این قضیه آن قدر مهم و محترم است که باید در یک مقاله جدا نیز به آن پرداخت! قضیه فیثاغورث طول دو ضلع قائمه مثلث قائم الزاویه را به طول وتر آن مربوط می کند. ممکن است در اینترنت فیثاغورس نیز ببینید اما بنظرم […]