از دیرباز، خطوط از بنیادی ترین عناصر در هندسه و اساس ترسیم های مربوط به آن است. به طوری که بسیاری از اشکال هندسی (همچون مثلث، مستطیل و…) که می شناسیم از اتصال خطوط محدود یا پاره خط ها به یکدیگر ایجاد می شوند. با این حال همانطور که دامنه کاربردی هندسه وسیع است؛ خطوط نیز گستره بزرگی از شاخه های دانش بشری را تحت الشعاع خود قرار می دهند. در نقشه کشی، معماری، هنر و… خط همواره نقشی کلیدی را ایفا می کند.

حال این مقدمه بلند، الزام می کند که اول ببینیم خط چیست. خط یک شیء هندسی، راست، بدون شکست و انحناست که از دو طرف تا بی نهایت امتداد دارد. چیزهای هندسی نیز داریم که همان کارکرد خط را در مقیاسی محدودتر ایفا می کنند. نیم خط، از یک نقطه شروع می شود و تا بی نهایت ادامه یابد. در نهایت پاره خط نیز یک نقطه را به نقطه دیگر متصل می کند. هردوی این ها تمام ویژگی های خط را به جز بی نهایت از دو طرف بدون را دارا می باشند.

شکل 4-1، از بالا به پایین، خط، نیم خط و پاره خط

همانطور که گفتیم چیزهای دارای انحنا مانند دایره خط نیستند.

شکل 4-2، اشکال دارای انحنا نه خط اند نه از خط ها ساخته شده اند.

1-4 نامگذاری خطوط

به طور معمول خط را با حروف کوچک لاتین نام گذاری می کنیم مانند $\overleftrightarrow{l}$. از هر دو نقطه خاص همواره تنها یک خط عبور می کند بنابراین می توان خط را با دو نقطه ای که از آن عبور می کند نیز نمایش داد $\overleftrightarrow{AB}$ (از یک نقطه همواره بی نهایت خط عبور می کند و یک نقطه برای نمایش یک خط مجزا کافی نیست). نیم خط نیز همانند خط است با این تفاوت که از نقطه ای که نیم خط شروع شده $C$، به سمت نقطه دیگر $D$ یک پیکان به این شکل رسم می شود $\overrightarrow{CD}$. پاره خط نیز به وسیله دو نقطه که به آن محدود شده نمایش می یابد مانند $\overline{EF}$.

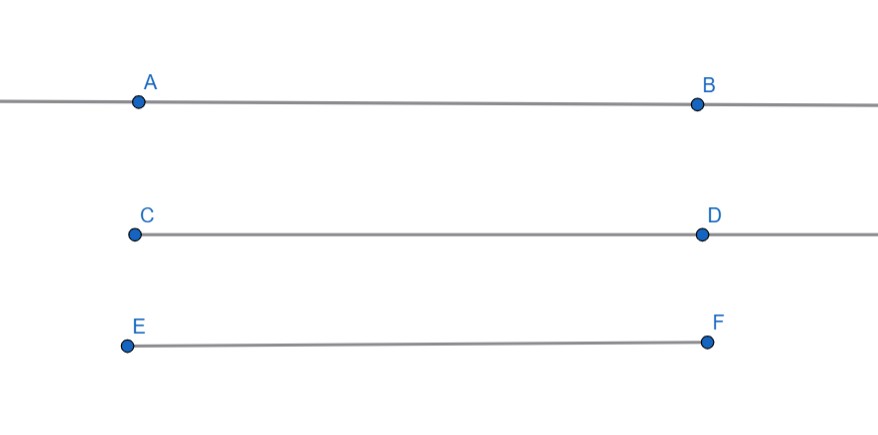
شکل 4-3، از بالا به پایین، خط $\overleftrightarrow{AB}$ ، نیم خط $\overrightarrow{CD}$ و پاره خط $\overline{EF}$.

2-4 چندضلعی

چندضلعی ها (یا صحیح تر، چندضلعی بسته) اشکالی اند که از اتصال چند پاره خط به هم، شکلی بسته را به وجود می آورند. به این صورت که برای ساخت یک چند ضلعی حداقل نیاز به سه پاره خط به هم متصل داریم که به هرکدام از این پاره خط ها ضلع می گوییم. شکل 4-4 چندضلعی های متنوعی ترسیم شده است.

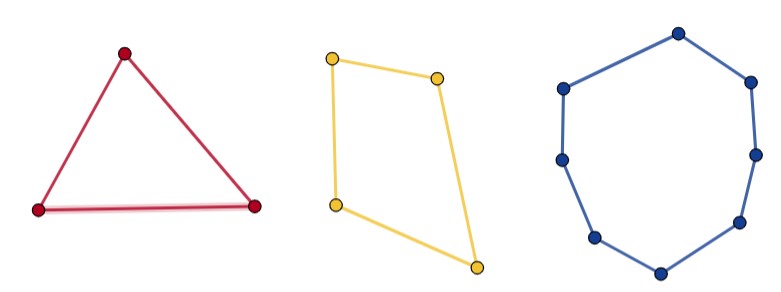
شکل 4-4، چندضلعی ها

3-4 برابری پاره خط ها

تساوی یا برابری پاره خط ها در یک شکل به وسیله علائم یکسان روی پاره خط های مساوی نمایش داده می شود. شکل 4-5، نمایش دهنده یک چهار ضلعی خاص یعنی متوازی الاضلاع است که در آن ضلع های روبه رو باهم برابرند و تساوی آن ها با یک خط و دو خط روی هرکدام نمایش یافته و از هم متمایز شده اند.

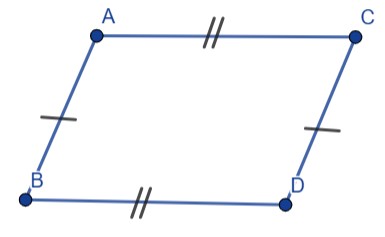
شکل 4-5، متوازی الاضلاعی که در آن به ترتیب $\overline{AB}=\overline{CD}$ و $\overline{AC}=\overline{BD}$ برقرار است.