دسته‌بندی: فیزیک

در فصل 72 با عملگرهای یکانی آشنا شدیم. در این فصل، به چگونگی تبدیل اسکالرها، کت ها، براها و عملگرها تحت تبدیلات یکانی می پردازیم.

در فصول قبل عملگرها، حالت ها و ویژگی های آن ها را بررسی نمودیم. بحث این فصل درباره چگونگی یافتن ویژه مقدار ها (Eigenvalues) و

در این فصل به وارون یک عملگر کوانتومی و عملگرهای یکانی می پردازیم. 1-72 وارون یک عملگر در صورتی که عملگر وارون پذیر باشد (همانند

در این فصل به بررسی توابع عملگرهای کوانتومی می پردازیم. 1-71 تعریف فرض کنید که $F(\hat{A})$ تابعی از عملگر $\hat{A}$ باشد. در صورتی که $\hat{A}$

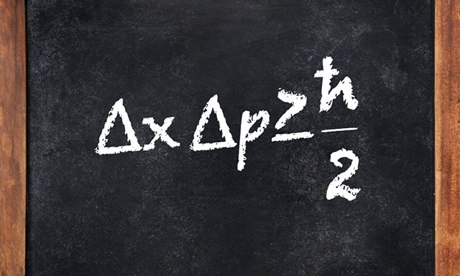
از کاربردهای جبر جابجاگر، محاسبه رابطه کلی برای حاصل ضرب عدم قطعیت های دو عملگر دلخواه است. رابطه ای که روابط عدم قطعیت هایزنبرگ را

در این فصل به جبر جابجاگر (Commutator Algebra) می پردازیم. 1-69 تعریف جابجاگر دو عملگر $\hat{A}$ و $\hat{B}$ با $[\hat{A},\hat{B}]$ نمایش داده می شود. جابجاگر به

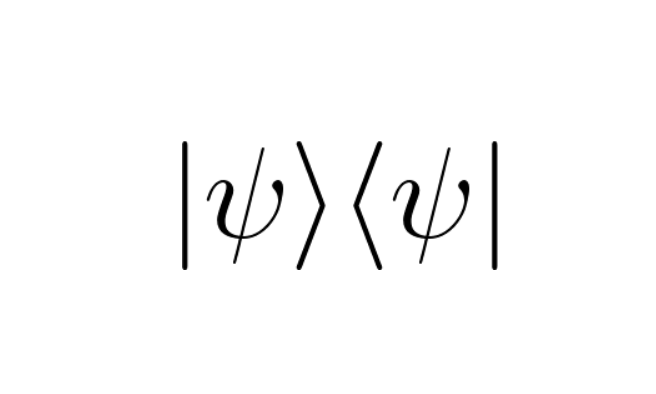
1-68 تعریف عملگر تصویر (projection operator)، عملگری هرمیتی است که با مجذور (مربع) خود برابر است. دو شرط زیر به طور کامل عملگر تصویر $\hat{P}$