دو چارچوب مرجع صلب $S$ و $S’$ را در نظر بگیرید که با سرعت نسبی $v$ حرکت یکنواخت دارند. همچنین برای چارچوب $S$ مختصات مکانی $x,y,z$ و برای چارچوب $S’$ مختصات مکانی $x’,y’,z’$ را داریم. دو مختصه زمانی $t$ و $t’$ نیز برای اندازه گیری زمان توسط دو چارچوب به کار می روند.

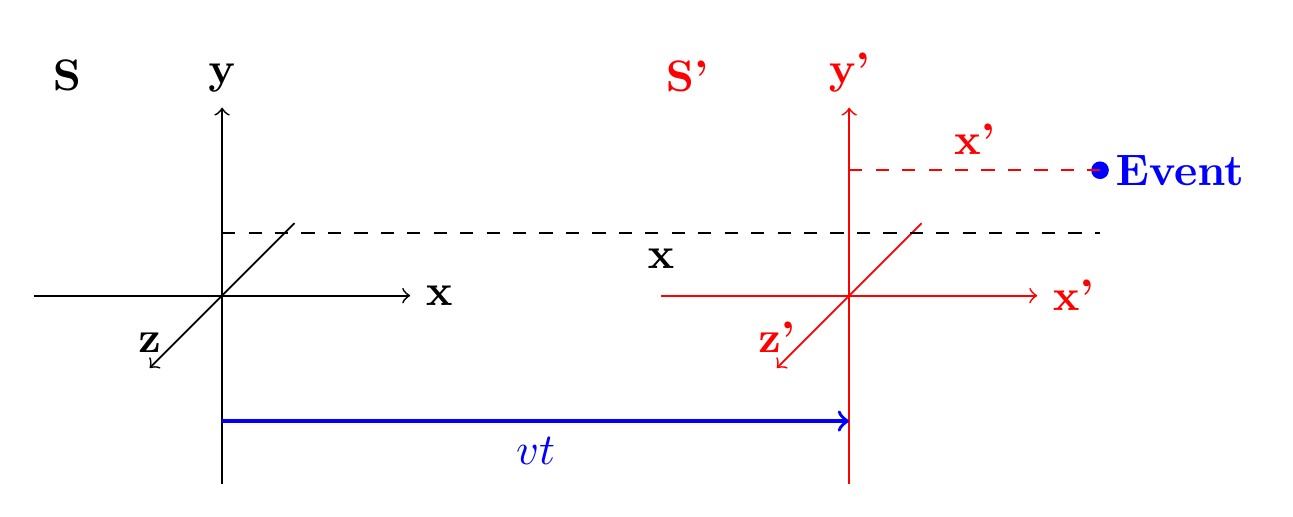
شکل 3-1، دو چارچوب مرجع $S$ و $S’$

1-3 پیکربندی استاندارد، رویداد و تبدیل گالیله

مطابق شکل 3-1، مبدأ چارچوب $S’$ با سرعت $v$ در امتداد محور $ x $ چارچوب $ S $ حرکت می‌کند (در جهت مثبت)، محور $ x’ $ با محور $ x $ منطبق است، در حالی که محورهای $ y $ و $ y’ $ موازی باقی می‌مانند، همان‌طور که محورهای $ z $ و $ z’ $ نیز موازی هستند. تمام ساعت‌ها هنگامی که دو مبدأ یکدیگر را ملاقات می‌کنند، روی صفر تنظیم می شوند. بنابراین، چارچوب های مختصاتی $ S: \{x, y, z, t\} $ و $ S’: \{x’, y’, z’, t’\} $ در پیکربندی استاندارد (standard configuration) قرار دارند.

فرض کنید رویدادی همانند چشمک زدن یک لامپ یا برخورد دو ذره نقطه‌ای دارای مختصات $ (x, y, z, t) $ نسبت به چارچوب $ S $ و مختصات $ (x’, y’, z’, t’) $ نسبت به دستگاه $ S’ $ باشد. در این صورت، تبدیل کلاسیک میان این دو دستگاه مختصاتی از تبدیلات گالیله استاندارد داده می شود:

$ \begin{equation} x’=x-vt \; , \; y’=y \; , \; z’=z \; , \; t’=t  \tag{3.1} \label{eq:3.1} \end{equation}$

سه رابطه فضایی از روی شکل 3-1 مشهود است زیرا که $x=x’+vt$ و دیگر مختصات فضایی نیز به شکل یکسانی بر دو محور هرکدام از چارچوب ها تصویر می شود. رابطه آخر مطلق بودن زمان و استقلال آن از چارچوب را نشان می دهد.

2-3 بردار سرعت و شتاب

مولفه های بردار سرعت در دو چارچوب مفروض به صورت زیر نوشته می شود:

$ \begin{equation} \displaystyle{\vec{u}=(\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}) \; , \; \vec{u’}=(\frac{dx’}{dt’},\frac{dy’}{dt’},\frac{dz’}{dt’})}  \tag{3.2} \label{eq:3.2} \end{equation}$

بنابراین کافی است از دو طرف تبدیلات گالیله ($\ref{eq:3.1}$) نسبت به زمان مشتق بگیریم زیرا می دانیم که $dt=dt’$:

$ \begin{equation} u’_{1}=u_{1}-v \; , \; u’_{2}=u_{2} \; , \; u’_{3}=u_{3} \tag{3.3} \label{eq:3.3} \end{equation}$

از آن جایی که $v$ تابع زمان نیست؛ می دانیم که تکرار عملیات بالا برای ($\ref{eq:3.3}$) شتاب نسبت به دو چارچوب را بدست می دهد که تمامی مولفه های آن در هردو چارچوب یکسان است. بنابراین می توان نتیجه را به شکل برداری زیر خلاصه نمود:

$ \begin{equation} \vec{r’}=\vec{r}-\vec{v}t \; , \; \vec{u’}=\vec{u}-\vec{v} \; , \; \vec{a’}=\vec{a} \tag{3.4} \label{eq:3.4} \end{equation}$

که در آن $\vec{a},\vec{v},\vec{r}$ به ترتیب بردار مکان، سرعت و شتاب در چارچوب $S$ هستند که معادل پریم دار آن ها برای چارچوب $S’$ در نظر گرفته شده است.

توجه کنید که دو چارچوب لخت الزاما در پیکربندی استاندارد قرار ندارند و به وسیله تبدیلات گالیله عمومی به یکدیگر تبدیل می شوند. تبدیلات گالیله عمومی صرفا ترکیبی از تبدیلات گالیله استاندارد به همراه دوران و انتقال فضایی یا انتقال زمانی است. این بدین معناست که دو دستگاه برهم انطباقی به شکل ذکر شده ندارند و نیز داریم با استفاده از دوران و انتقال فضایی یا زمانی این دو را بر هم منطبق سازیم تا پیکربندی استاندارد شود.

3-3 نسبیت نیوتنی

به یاد داریم هرگاه چارچوب صلبی قانون اول نیوتن در آن برقرار باشد؛ آنگاه چارچوبی لخت است. فرض کنیم چارچوب $S$ شکل 3-1 چارچوبی لخت است. در این صورت چارچوب $S’$ نیز لخت خواهد بود. زیرا که طبق رابطه ($\ref{eq:3.3}$)، سرعت های ثابت در $S$ به سرعت های ثابت در $S’$ مبدل می شوند. بنابراین هر ذره آزاد در $S$ را ذره ای آزاد در $S’$ درک می کنیم.

از طرف دیگر، تنها چارچوب‌ هایی که با سرعت ثابت نسبت به $S$ حرکت می‌کنند می‌توانند لخت باشند؛ زیرا نقاط ثابت در هر چارچوب اینرسی، ذرات آزادی فرضی محسوب می‌شوند. بنابراین همه باید به‌طور یکنواخت نسبت به $S$ حرکت کنند. هیچ مجموعه‌ ای از ذرات آزاد نمی‌تواند صلب باقی بماند مگر اینکه همه سرعت‌های آن‌ها یکسان باشند زیرا باید فاصله خود از همدیگر را حفظ نمایند. بنابراین، دسته‌ چارچوب‌ های لخت شامل تمام چارچوب‌ های صلبی است که به‌طور یکنواخت نسبت به یک چارچوب لخت شناخته‌شده حرکت می‌کنند. این چارچوب شناخته شده می تواند فضای مطلق باشد.

علاوه بر قانون اول، قانون دوم و سوم نیز در تمامی چارچوب های لخت برقرارند. در نظریه نیوتن نیرو و جرم، مطابق اصل موضوع، میان چارچوب های لخت ناورداست و ناوردایی شتاب تحت تبدیل گالیله از ($\ref{eq:3.4}$) مشخص است. برقراری قوانین نیوتن در تمامی چارچوب های لخت، نسبیت نیوتنی یا گالیله ای می گوییم. گالیله پیش از نیوتن این را مطرح کرده بود که اگر با یک کشتی در آب های آرام حرکت کنیم (که تقریبا حرکتی یکنواخت است)؛ حرکات و قوانین را همانطور دریافت می کنیم که در حالت سکون کشتی می دیدیم.