فضای مطلق ایده ای زیربنایی برای نظریات نیوتن بود. نیوتن این گونه استدلال میکرد که اجزای فضا بخش هایی بدون تغییر مکانی و با جایی مشخص هستند و جابجاشدن مکانی از خودش بی معناست. او استدلال مشابهی را در مورد مطلق بودن زمان و ثابت بودن اجزای آن مطرح می کرد: اگر دیروز و فردا نسبت به بقیه‌ زمان جایگاه‌ های خود را عوض کنند؛ آنگاه دیروز به امروز و امروز به دیروز تبدیل می‌شود. بنابراین، نیوتن دیدگاهی جامع نسبت به هردو مقوله فضا و زمان داشت.

از آنجایی که اجزای فضا با حواس ما قابل دیدن یا از یکدیگر قابل تشخیص نیستند؛ به جای آنها از اندازه‌گیری‌های حسی بهره می‌بریم. زیرا از موقعیت‌ها و فواصل موجودات نسبت به هر جسمی که به‌عنوان جسمی ثابت در نظر گرفته می‌شود، تمامی مکان‌ها را تعریف می‌کنیم و سپس بر اساس همان مکان‌ها، همه‌ی حرکات را محاسبه می نماییم به‌ شکلی که انتقال اجسام از برخی از آن مکان‌ها به سایر مکان‌ها در نظر گرفته می‌شوند. از این رو، به جای مکان‌ها و حرکات مطلق، از مکان‌ها و حرکات نسبی استفاده می‌کنیم؛ و این امر در امور روزمره هیچ مشکلی ایجاد نمی‌کند. اما در مباحث فلسفی، لازم است از حواس خود جدا شده و اجسام را به ذاتشان در نظر گیریم، جدا از آنچه صرفا معیارهای قابل حس آن‌ها محسوب می‌شود. زیرا ممکن است هیچ جسمی به‌طور واقعی در حالت سکون وجود نداشته باشد که مکان‌ها و حرکات سایر موجودات نسبت به آن تعریف گردد.

General Scholium – آیزاک نیوتن

بنابراین ویژگی های چنین فضایی از نظر نیوتن، یک فضای سه بعدی اقلیدسی است که با زمان تغییری نمی کند. همچنین ساختاری محکم و سخت دارد که تغییرات مکانی در آن اتفاق نمی افتد. حرکت حقیقی حرکتی است که نسبت به چنین فضایی صورت گیرد. چنین حرکت حقیقی و مطلقی نیاز به ادله ای تجربی برای استحکام داشت که نیوتن آزمایش سطل خود را پیشنهاد می دهد.

1-4 سطل نیوتن

در تبدیل گالیله دیدیم که شتاب مطلق است و به چارچوب یا ناظر اندازه گیری وابستگی ندارد. بدین صورت همواره می توان شتاب مطلق را تعیین نمود و نیوتن آن را شتاب نسبت به فضای مطلق تفسیر می کرد. در این آزمایش سطلی پر از آب را در نظر می گیریم که به وسیله طنابی آویزان شده. سپس سطل را به آرامی چرخانده و رها می کنیم.

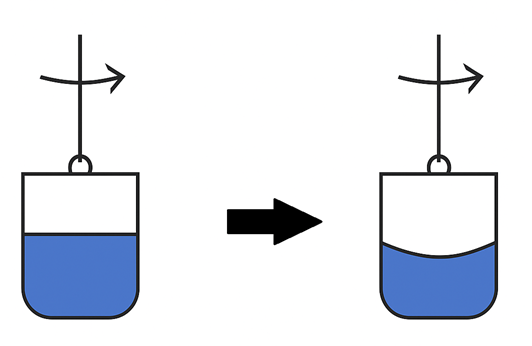
شکل 4-1، آزمایش سطل نیوتن، مرحله اول سمت چپ و مرحله دوم سمت راست به تصویر کشیده شده است.

مرحله اول: آب داخل سطل بدلیل لختی خود نمی چرخد؛ با این حال دیواره سطل نسبت به آن حرکت نسبی دارد. بنابراین آب نسبت به چارچوب سطل شتاب دوران گرفته. در این مرحله سطح آب صاف باقی می ماند.

مرحله دوم: به تدریج پس از مدتی به دلیل اصطکاک میان آب و سطل، آب نیز همراه با سطل شروع به حرکت می کند و در اثر نیروی گریز از مرکز، قطرات آب به سمت دیواره ظرف هدایت می شود. در این مرحله سطح آب گود یا سهمی شکل می شود. این حالتی پایدار است و در حالت پایدار همواره نیرو عمود بر سطح سیال خواهد بود. دیاگرام نیرو در شکل 4-2 به تصویر کشیده شده است.

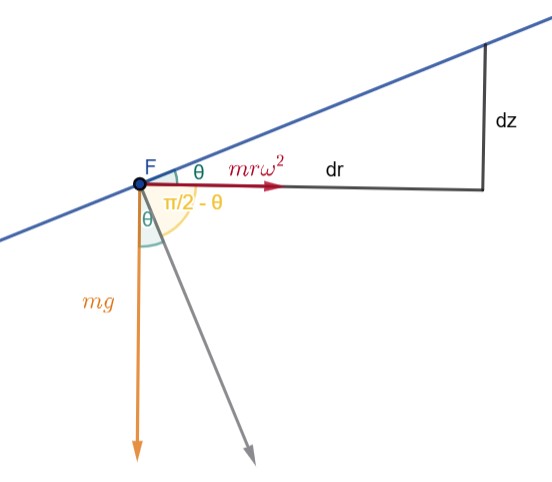
شکل 4-2، برای یک ذره آب، نیروی مرکزگرا با رنگ قرمز، نیروی گرانش با رنگ نارنجی و نیروی برایند عمود بر سطح آب با رنگ خاکستری نمایش داده شده. همچنین دو عنصر دیفرانسیلی $dz$ و $dr$ نیز با زاویه بین $dr$ و سطح آب یعنی $\theta$ نشان داده شده. این زاویه، مطابق شکل زاویه میان نیروی برایند و نیروی گرانشی نیز هست.

مطابق شکل 4-2 داریم:

$ \begin{equation} \displaystyle{\tan{\theta}=\frac{dz}{dr}=\frac{mr\omega^2}{mg}}\tag{4.1} \label{eq:4.1} \end{equation}$

بنابراین با انتگرال گیری خواهیم داشت:

$ \begin{equation} \displaystyle{\int{dz}=\int{\frac{\omega^2}{g}r \; dr}+C}\tag{4.2} \label{eq:4.2} \end{equation}$

که با در تغییر نام $C=z_0$ خواهیم داشت:

$ \begin{equation} \displaystyle{z(r)=\frac{\omega^2}{2g}r^2+z_0}\tag{4.3} \label{eq:4.3} \end{equation}$

به این صورت یک سهمی بر سطح آب داریم که همان چیزی است که نیوتن مدنظر داشت. نیوتن بدین شکل استدلال کرد؛ در مرحله اول، اگرچه آب نسبت به سطل (یا چارچوب آن) شتاب دورانی دارد؛ نسبت به فضای مطلق هنوز شتاب نگرفته و حرکت نکرده است. حرکت حقیقی در مرحله دوم رخ می دهد و نشانه شتاب گرفتن نسبت به فضای مطلق، ظهور نیروی گریز از مرکز بر قطرات آب است پس فضای مطلق و حرکت مطلق وجود دارد. ایده فضا و حرکت مطلق و آزمایش سطل، زمینه ساز بحث های متعدد فلسفی و فیزیکی توسط آیندگان نیوتن شد که بعدتر به آن خواهیم پرداخت.