
49 انتگرال : توابع مثلثاتی
در بحث مشتق گیری با مشتق روابط مثلثاتی آشنا شدیم. همانطور که دیدیم خود توابع مثلثاتی هستند که عملیات مشتق گیری بر آنها، توابع مثلثاتی

در بحث مشتق گیری با مشتق روابط مثلثاتی آشنا شدیم. همانطور که دیدیم خود توابع مثلثاتی هستند که عملیات مشتق گیری بر آنها، توابع مثلثاتی
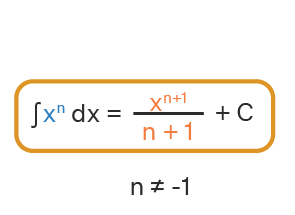
همانطور که در مشتق گیری با چندجمله ای های توانی کار را آغاز کردیم؛ ابتدا بهتر است با نحوه انتگرال گیری از این نوع عبارات
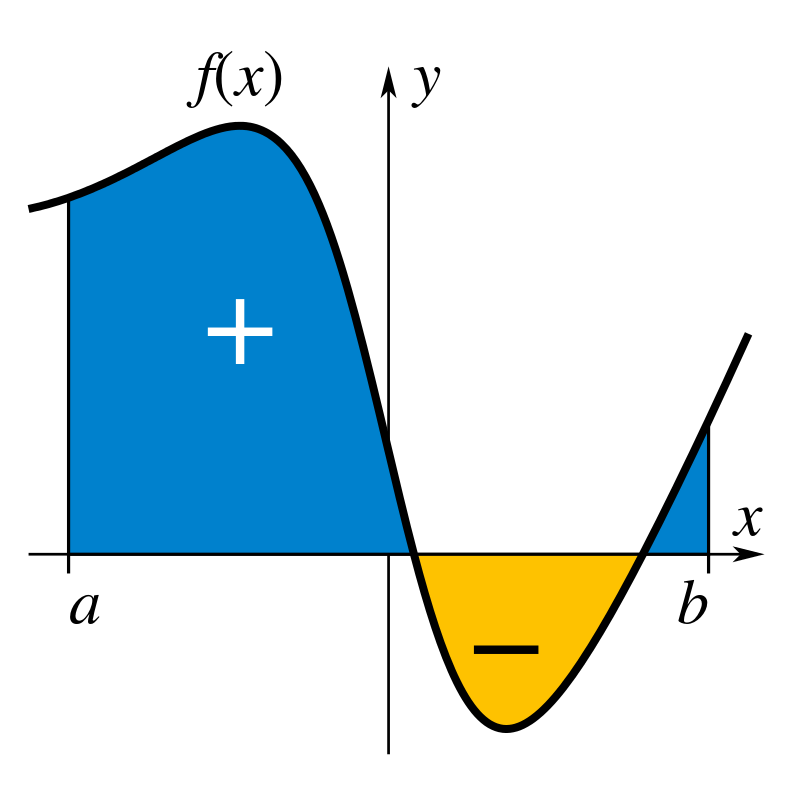
پس از سلسله مباحث مشتق، حالا آماده ایم با مفهوم انتگرال آشنا شویم. انتگرال را می توان از دو دیدگاه بررسی کرد؛ اول اینکه انتگرال

در فصول قبل با توابع نمایی و لگاریتمی آشنا شدیم. اکنون زمان آن رسیده که به مشتق آنها بپردازیم. تابع نمایی طبیعی $e^{x}$ یک خاصیت

در این فصل، به طریقه ای از محاسبه حدهای مبهم می پردازیم که با مشتق گیری از دو تابع صورت و مخرج صورت می پذیرد.
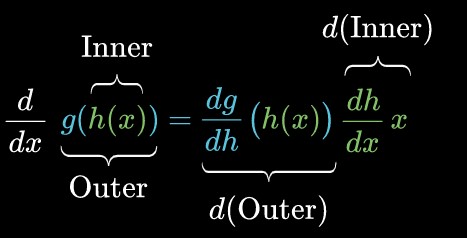
در این فصل، قصد آشنایی با مشتق ترکیب توابع را داریم. ابتدا به این موضوع خواهیم پرداخت که توابع چگونه در یکدیگر ترکیب می شوند