پس از سلسله مباحث مشتق، حالا آماده ایم با مفهوم انتگرال آشنا شویم. انتگرال را می توان از دو دیدگاه بررسی کرد؛ اول اینکه انتگرال را می توان به عنوان عملیاتی معکوس مشتق درک کرد و دوم اینکه بوسیله انتگرال، مقدار مساحت زیر منحنی ها در دستگاه مختصات قابل محاسبه است که به ما در محاسبه مساحت بسیاری از اشکال پیچیده یاری می رساند.

1-47 انتگرال نامعین یا پادمشتق

از مشتق عبارات تواندار بخاطر داریم که می توان از تابع اولیه $x^{2}$ مشتق گرفت و به تابع مشتق $2x$ رسید. همین طور که در مقدمه این فصل گفتم، می توان به عملیاتی فکر کرد که با اعمال آن برا تابع مشتق $2x$ به ما تابع اولیه $x^2$ را تحویل دهد. این عملیات را می توان پادمشتق نامید چون عکس مشتق است. البته باید این را هم درنظر گرفت که تنها تابعی که حاصل مشتق آن $2x$ باشد؛ $x^{2}$ نیست. مشتق اعداد ثابت همیشه صفر است پس می توان تابع اولیه مذکور را همیشه با مقداری ثابت جمع کرد. بدین ترتیب تابع اولیه ما $x^{2}+C$ خواهد بود. این عملیات را انتگرال نامعین می نامیم.

2-47 نمادگذاری انتگرال نامعین

فرض کنید تابعی مثل $F(x)$ داریم که مشتق آن $f(x)$ باشد. آنگاه می توان از $f(x)$ انتگرال نامعین برحسب $x$ گرفت تا تابع اولیه به علاوه مقداری ثابت، حاصل آن باشد: $F(x)+C$. انتگرال نامعین توصیف شده را به صورت زیر است:

(1)

$\large \int{f(x)\mathrm{d}x}=F(x)+C$

علامت $\int$ به معنای انتگرال گیری نامعین و عبارت $\mathrm{d}x$ به معنای انتگرال گیری از متغیر $x$ است. بدین وسیله می توان از تابع شیب ها (مشتق)، به رفتار تابع اولیه پی برد. برای مثالی که در بخش 47-1 ذکر شد، انتگرال به صورت زیر است:

(2)

$\large \int{2x\mathrm{d}x}=x^{2}+C$

3-47 انتگرال معین

انتگرال معین در محاسبه مساحت زیر منحنی در دستگاه مختصات کاربرد دارد. شیوه کار به این صورت است که می توان سطح زیر هر منحنی را به مستطیل های بسیار کوچک تقسیم کرد و جمع این مساحت ها، سطح زیر منحنی را بدست می دهد.

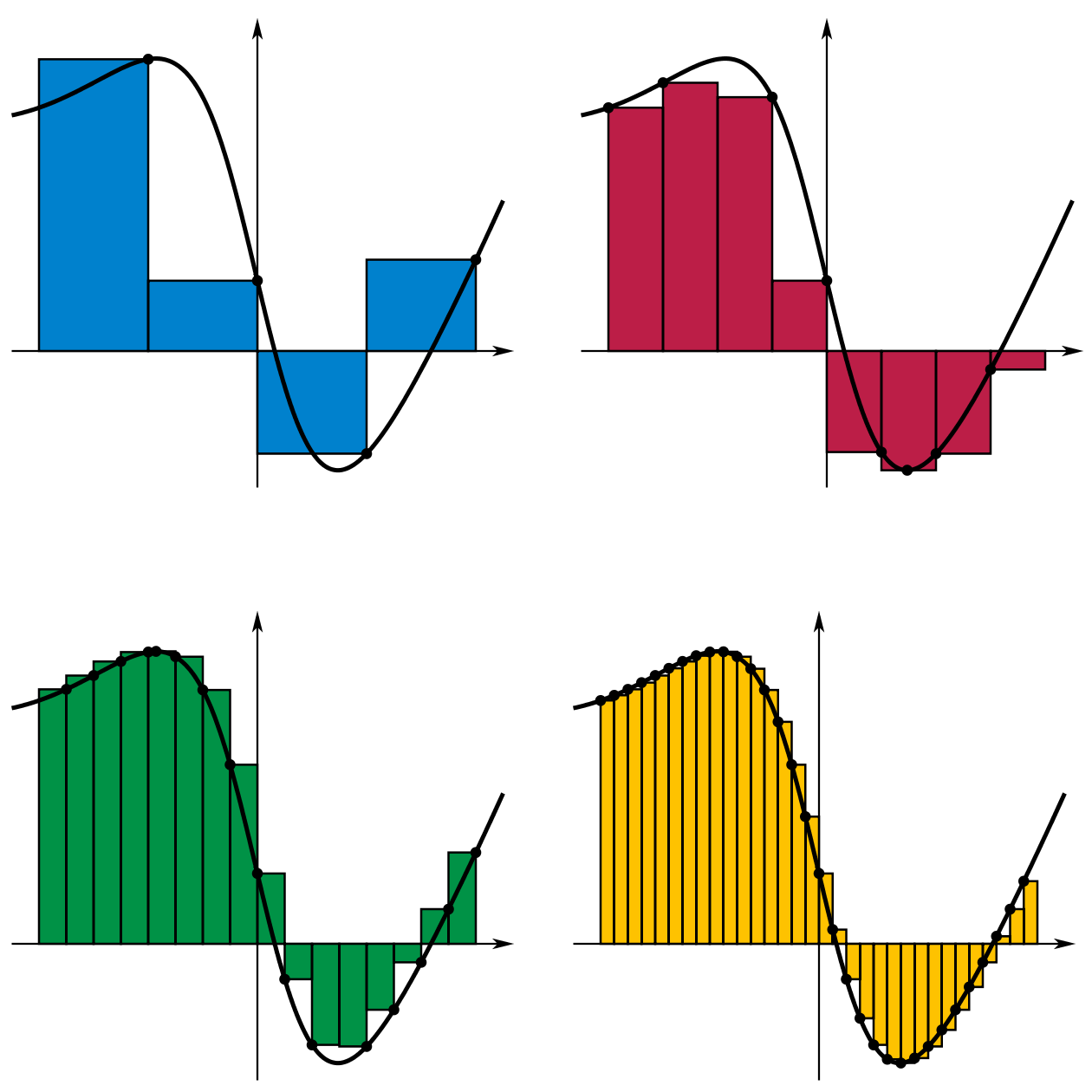
شکل 47-1، با کوچکتر شدن عرض هر مستطیل، مساحت زیر منحنی دقیق تر بدست می آید.

مساحت زیر منحنی با رابطه $y=f(x)$ که $F(x)$ تابع اولیه آن است، در بازه $x=a$ تا $x=b$ از رابطه زیر بدست می آید ($b>a$):

(3)

$\large \int^{b}_{a} f(x) \mathrm{d}x = F(b)-F(a)$

این همان چیزی است که انتگرال معین نام دارد. در محاسبه مساحت زیر منحنی باید دو نکته مهم را درنظر بگیریم، نخست اینکه مساحت علامت دارد. هرگاه منحنی از محور $x$ بالاتر بود، مساحت زیر آن مثبت و هرگاه منحنی از محور $x$ پایین تر بود، مساحت بالای آن منفی است.

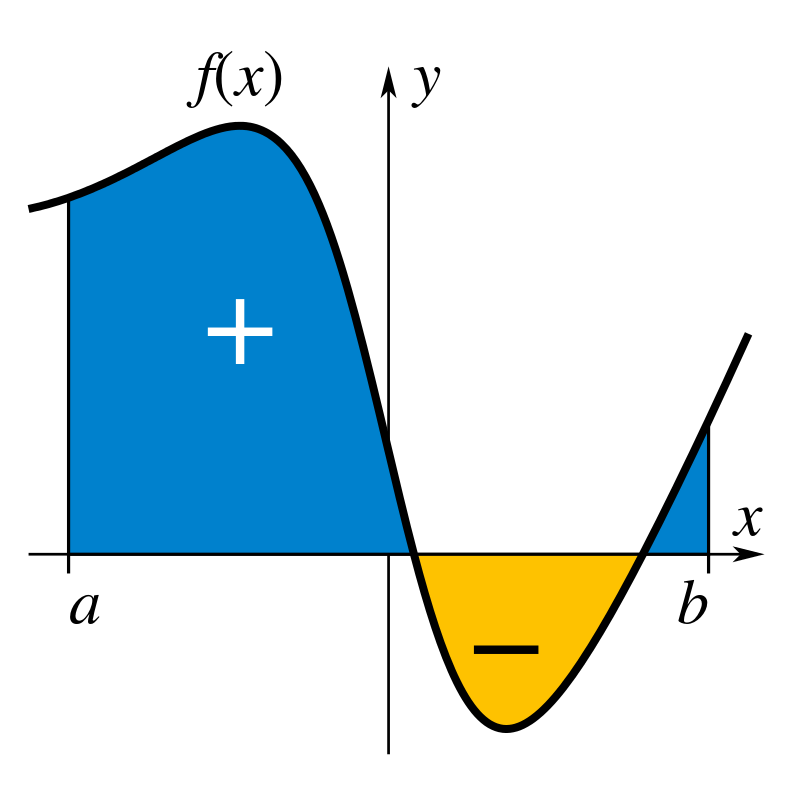
شکل 47-2، علامت دار بودن مساحت

دیگر نکته قرینه بودن مساحتی که $x$ آن از راست به چپ تغییر می کند (از $x$ بزرگتر به $x$ کوچکتر) با مساحتی است که $x$ آن از چپ به راست تغییر می کند (از $x$ کوچکتر به $x$ بزرگتر)، این را می توان از رابطه (3) نیز نشان داد:

(4)

$\large \int^{a}_{b} f(x) \mathrm{d}x = F(a)-F(b)$

طرف راست دو تساوی رابطه (3) و (4) قرینه یکدیگرند پس طرف چپ نیز چنین شرایطی را داراست:

(5)

$\large \int^{b}_{a} f(x) \mathrm{d}x = -\int^{a}_{b} f(x) \mathrm{d}x$

*مثال 47-1)

مساحت زیر نمودار $y=2x$ را در بازه $(-1,2)$ به دو روش هندسی و انتگرال معین بدست آورید.

پاسخ

مطابق شکل 47-3، محاسبه مساحت دو مثلث به روش هندسی کافی است. فقط باید دقت کنیم که مساحت بالای منحنی منفی است.

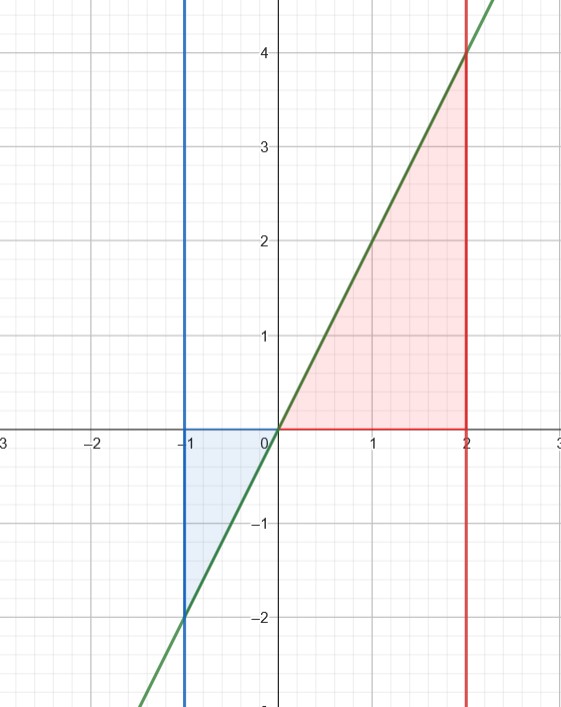
شکل 47-3، پاسخ مثال 47-1

مساحت بخش قرمز $\frac{1}{2}\times 2 \times 4=4$ و مساحت بخش آبی (که در واقع منفی است) برابر با $\frac{1}{2}\times 1 \times 2=1$ است. بدین ترتیب مساحت کل برابر با $4-1=3$ است.

تابع اولیه $y=2x$ را از رابطه (2) می دانیم، بنابراین انتگرال معین به صورت زیر نوشته می شود:

$\large \int^{2}_{-1} 2x \mathrm{d}x=x^2 |^{x=2}_{x=-1}=(4)-(1)=3$

4-47 خواص انتگرال

در اینجا ذکر دو خاصیت مهم ضروری است. فرض کنید از مجموع دو تابع f(x) و g(x) انتگرال می گیریم. این انتگرال گیری در یک بازه مشخص، با اینکه از هرکدام انتگرال بگیریم و سپس نتیجه نهایی را جمع کنیم تفاوتی ندارد:

(6)

$\large \int^{b}_{a} f(x)+g(x) \mathrm{d}x= \int^{b}_{a} f(x) \mathrm{d}x+ \int^{b}_{a} g(x) \mathrm{d}x$

دیگر خاصیت این است که می توان ضریبی مانند $k$ که عدد ثابت است و به متغیر انتگرال گیری وابستگی ندارد را از انتگرال خارج کرده و در حاصل ضرب کرد (چنین چیزی برای عدد ثابتی که با تابع جمع می شود امکان پذیر نیست):

(7)

$\large \int^{b}_{a} kf(x) \mathrm{d}x=k\int^{b}_{a} f(x) \mathrm{d}x$

5-47 جمع بندی فصل

در این فصل، با انتگرال نامعین و معین آشنا شدیم و پی بردیم که عمل پادمشتق و سطح زیر منحنی (یا شاید به بیان بهتر سطح میان منحنی و محور $x$) چگونه به یکدیگر مربوط می شوند.

*1- از رابطه $f(x)=3x^3$ مشتق بگیرید. سطح زیر نمودار تابع مشتق $f'(x)$ را در بازه $(-2,2)$ به وسیله انتگرال معین بدست آورید.