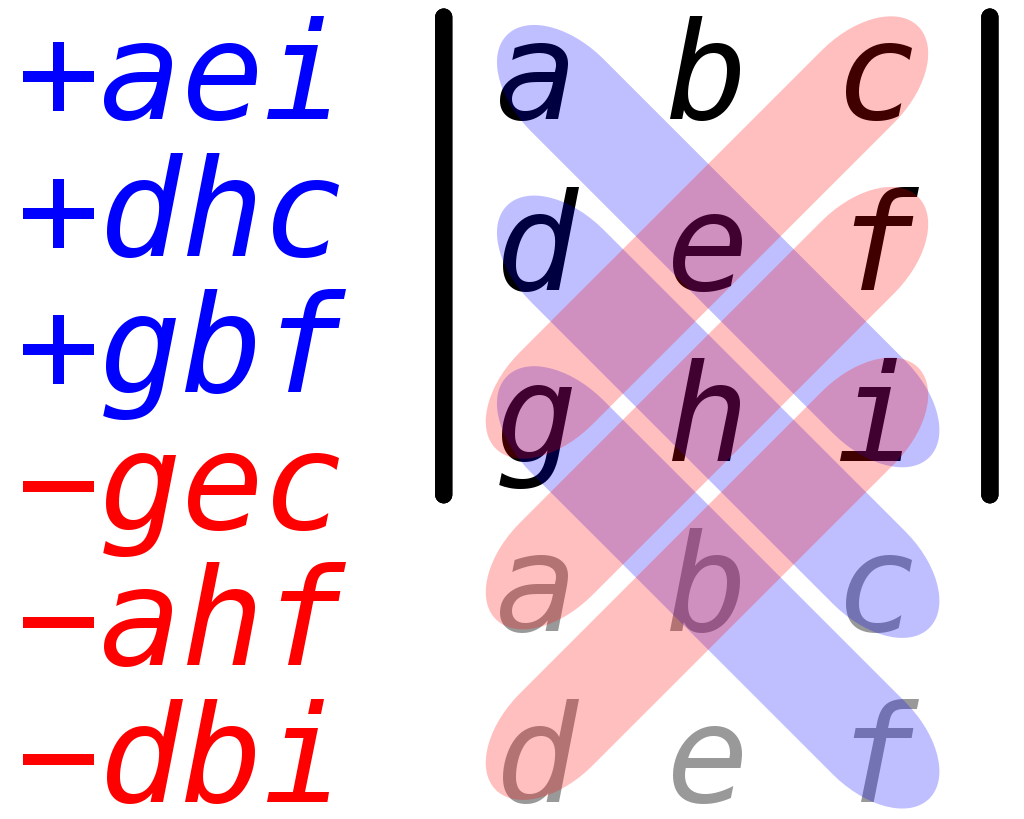
55 ماتریس : دترمینان
دترمینان (determinant) مفهومی کاربردی در محاسبات ماتریسی است. پس از آشنایی با ماتریس و عملیات های آن، خوب است که با دترمینان آشنا شویم. همانند

دترمینان (determinant) مفهومی کاربردی در محاسبات ماتریسی است. پس از آشنایی با ماتریس و عملیات های آن، خوب است که با دترمینان آشنا شویم. همانند
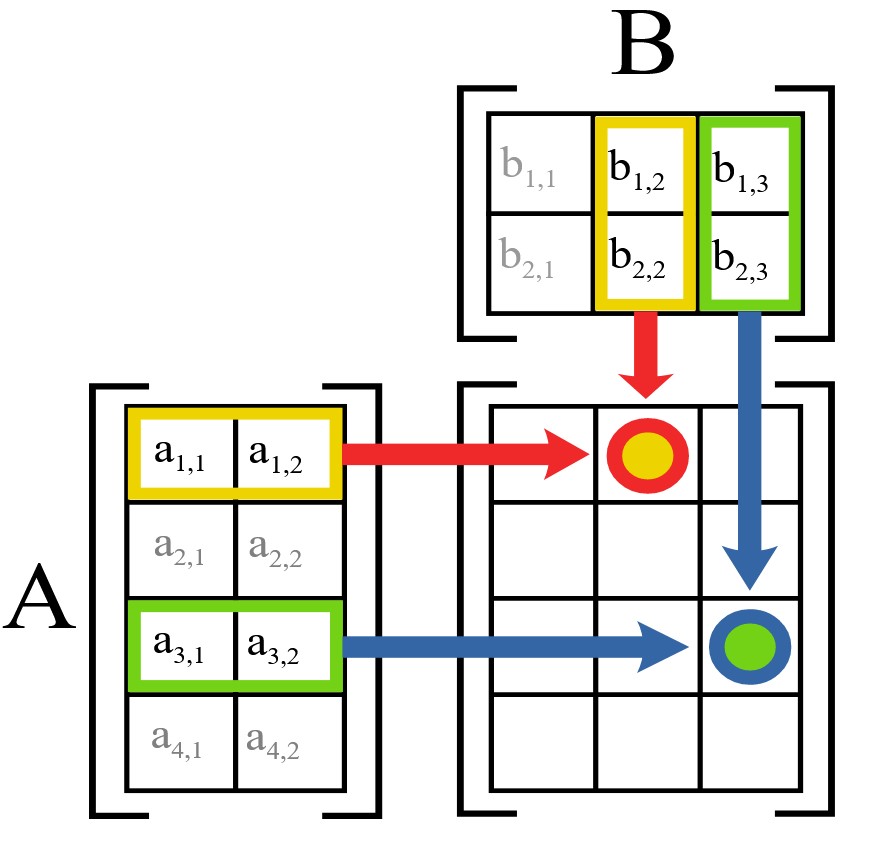
ضرب ماتریسی موضوع این فصل است. پس از آشنایی با مقدمات ماتریس، فراگیری الگوریتم ضرب دو ماتریس حائز اهمیت است. روش ضرب ماتریس ها سرراست

یکی از موضوعات جالب و کاربردی ریاضی، ماتریس (Matrix) است که در جایجای فیزیک، ریاضیات و علوم کامپیوتر ظاهر می شود. بخصوص که ماتریس نقش
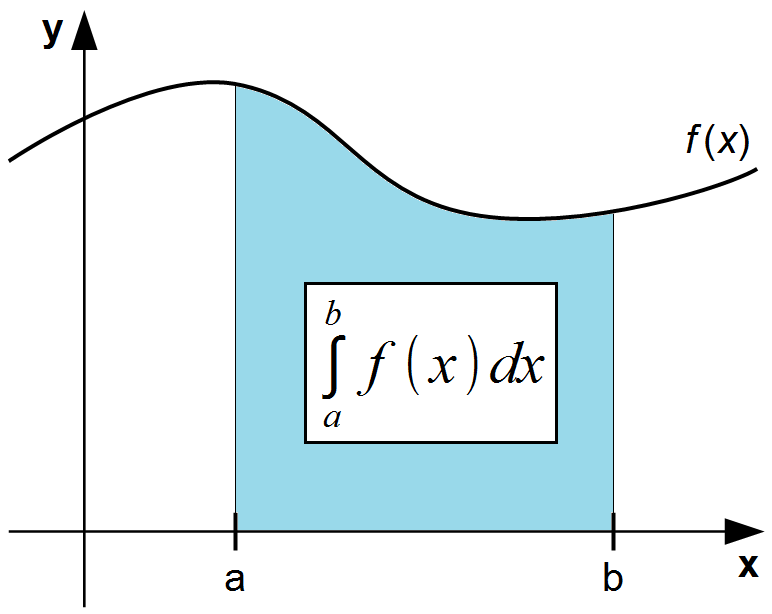
یکی از روش های کارآمد برای حل طیف گسترده ای از انتگرال های پیچیده، روش تغییر متغیر و تبدیل انتگرال به انتگرال های ساده ای

انتگرال گیری جزء به جزء، روشی است که بوسیله آن می توان برخی از انتگرال های حاصل ضرب توابع (که ظاهر دشواری دارند) به سادگی

در این فصل قصد داریم به انتگرال تابع نمایی و لگاریتمی بپردازیم. مطابق معمول، انتگرال را به چشم پادمشتق می بینیم و با استفاده از