این فصل قصد دارم به یکی از اساسی ترین مفاهیم ریاضی ورود کنم. مجموعه را می توان دسته بندی اشیائی مشخص و غیرتکراری نامید که ترتیب اعضا در آن اهمیتی ندارد. مشخص بودن در اینجا بدین معنی است که عضویت آن شی در مجموعه مبهم یا قابل جایگزینی نباشد. مثلا کشورهای قهرمان در جام جهانی فوتبال یک مجموعه مشخص و متمایز است اما مجموعه ای تحت عنوان سه فیلسوف یونانی دارای ابهام است. می توان ارسطو، افلاطون و سقراط را یک مجموعه گرفت و زنون، اپیکور و دموکریت را یک مجموعه دیگر. پس عبارت “سه فیلسوف یونانی” بیانگر یک مجموعه نیست؛ چون مجموعه یکتایی را توصیف نمی کند. در مورد غیرتکراری و بدون ترتیب بودن نیز می توان مجموعه را با دنباله مقایسه کرد. در مجموعه تکرار اعضا و عوض کردن ترکیب مجموعه، مجموعه جدیدی را تولید نمی کند اما در دنباله کاملا برعکس بود.

1-21 نمایش

در ریاضیات بیشتر با مجموعه هایی کار داریم که تمام اعضای آن عدد هستند. یک نوع نمایش مجموعه، نمایش بوسیله کروشه است. مثلا مجموعه ای به نام A شامل سه عدد 1 و 2 و 3 را به صورت زیر نمایش می دهیم:

(1)

$\large A=\left \{ 1,2,3 \right \} $

نمایشی دیگر که به جان ون، ریاضی دان بریتانیایی نسبت داده می شود، نمودار ون است؛ این نمایش به این صورت است که دور اعداد عضو مجموعه یک منحنی رسم می شود که نشانگر مجموعه موردنظر است؛ برای مجموعه A داریم:

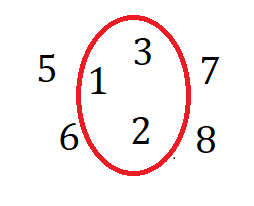
شکل 1-21، نمودار ون مجموعه A

روش دیگری نیز وجود دارد که نمایش ضابطه ای اعضای مجموعه است؛ چیزی شبیه جمله عمومی در دنباله. فرض کنید $\mathbb{Z}$ مجموعه اعداد صحیح است؛ نمایش مجموعه A به صورت زیر خواهد بود:

(2)

$\large A=\left \{ x \in \mathbb{Z}\mid 1\leq x\leq 3 \right \}$

عبارت بالا به این معنی است که x هایی که هم عضو مجموعه اعداد صحیح اند هم بزرگتر مساوی 1 و کوچکتر مساوی 3 هستند که به همان نتیجه نمایش کروشه (1) منجر می شود.

* مثال 21-1)

مجموعه اعداد فرد را نمایش دهید.

پاسخ

مجموعه اعداد فرد، مجموعه اعداد صحیحی است که بر 2 بخش پذیر نیستند(در بعضی منابع علاوه بر شرط صحیح بودن، مثبت بودن نیز لحاظ شده). نمودار ون بیشتر برای نمایش مجموعه هایی با تعداد اعضا کم کاربرد دارد؛ به همین دلیل از نمایش ضابطه ای و کروشه ای بهره می بریم:

$\large A=\left \{ 2x-1 \mid x \in \mathbb{Z} \right \}$

نمایش بالا به این معنی است که تمامی اعضای $\mathbb{Z}$ را دو برابر و سپس منهای یک کن!

$\large O=\left \{ …,-3,-1,1,3,… \right \} $

2-21 مجموعه تهی

البته الزاما یک مجموعه دارای عضو نیست. می تواند خالی و بدون عضو باشد. به این مجموعه، مجموعه تهی می گویند. نمایش آن به صورت زیر است و با $\varnothing$ نمایش می دهند.

(3)

$\large \varnothing=\left \{ \right \} $

3-21 جمع بندی فصل

در این فصل، با مفهوم مجموعه و سه راه نمایش آن آشنا شدیم. با کاربردهای این نمایش ها در مباحث پیشرفته تر بیشتر آشنا خواهیم شد. این مفهوم که پایه و اساس بسیاری از نظریات قرن اخیر ریاضی است؛ نخستین بار توسط گئورگ کانتور، ریاضی دان آلمانی به کار گرفته و مطالعه شد.

شکل 21-2، گئورگ کانتور (1845 میلادی – 1918 میلادی)

*1- مجموعه اعداد زوج را به روش ضابطه ای نمایش دهید.

*2- مشخص کنید هرکدام از مفاهیم زیر بیانگر یک مجموعه هستند یا خیر.

الف) سه نویسنده ایرانی

ب) مدال آوران ایران در بازی های المپیک

پ) فهرست افرادی که گواهینامه رانندگی دارند

ت) سیارات سامانه خورشیدی(منظومه شمسی)

*3- تعداد اعضای دو مجموعه زیر را مشخص کنید:

$\large A={1,5,4,5}$

$\large B={4,8,\sqrt{16},\frac{24}{3},-2}$