فصل قبل با مفاهیم پایه ای مجموعه آشنا شدیم. در این فصل مفهوم زیرمجموعه را می شکافیم! از نام زیرمجموعه مشخص است که به یک مجموعه بزرگتر و جامع تر از خودش مربوط می شود؛ درست است. بنابه تعریف، مجموعه B زمانی زیرمجموعه A است که تمامی اعضای B در A حضور داشته باشند.

1-22 تعریف

گفتیم که اگر تمامی اعضای مجموعه B در مجموعه A باشد؛ آنگاه B زیرمجموعه A است. این گزاره را به شکل زیر نشان می دهیم:

(1)

$\large B\subseteq A $

نماد $\subseteq$ به معنی زیرمجموعه بودن است. واضح است اگر تنها یک عضو B در A نباشد؛ دیگر B زیرمجموعه A نیست؛ این گزاره به صورت زیر بیان می شود:

(2)

$\large B \nsubseteq A $

* مثال 22-1)

یک زیرمجموعه برای مجموعه $A= \left \{ 1,2,3 \right \}$ مثال بزنید.

پاسخ

باید همه اعضای زیرمجموعه در مجموعه A موجود باشد. پس من $B= \left \{ 2,3 \right \}$ را مثال می زنم. در نمایش به شکل نمودار ون هم دقت کنید که منحنی زیرمجموعه کامل درون منحنی مجموعه قرار بگیرد:

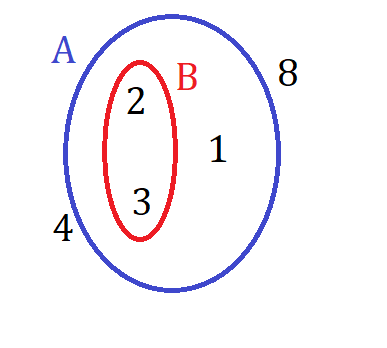
شکل 22-1، نمودار ون مثال 22-1

2-22 خواص

چند خاصیت مشهور در مبحث زیرمجموعه ها وجود دارد. مجموعه تهی را که یادتان هست. تهی زیر مجموعه تمامی مجموعه هاست. برای شهودی نسبی می توان گفت تهی عضوی ندارد. هر مجموعه دیگر نیز حداقل هیچ عضوی ندارد. پس هیچوقت امکان ندارد عضوی در تهی بیابیم که در یک مجموعه دیگر نباشد. برای یک مجموعه دلخواه مثل A داریم:

(3)

$\large \varnothing \subseteq A $

دیگر مورد قابل ذکر این است که هرمجموعه ای زیرمجموعه خودش است:

(4)

$\large A \subseteq A $

بنابر چیزی که گفتم، برای اینکه برابری دو مجموعه را نشان دهیم؛ کافی است اثبات کنیم هریک از مجموعه ها زیرمجموعه دیگری است:

(5)

$ \large B\subseteq A , A\subseteq B \Leftrightarrow A=B $

3-22 تعداد زیرمجموعه ها

تعداد کل زیرمجموعه های هرمجموعه از تعداد اعضای آن مجموعه قابل محاسبه است؛ اگر مجموعه دلخواه A دارای n عضو باشد؛ تعداد زیرمجموعه های آن برابر $2^{n}$ است و به صورت زیر نشان داده می شود:

(6)

$ \large N(P(A))=2^{n}$

در رابطه بالا، P(A) مجموعه ای است که هر زیرمجموعه A، یکی از اعضای آن است. به این مجموعه، مجموعه توانی A گفته می شود. (در فصل 21 گفتیم اغلب با مجموعه هایی کار می کنیم که اعضای آن عدد هستند؛ اما مشکلی بوجود نمی آید اگر عضو یک مجموعه، خود نیز مجموعه باشد)

* مثال 22-2)

مجموعه توانی $A= \left \{ 1,2,3 \right \}$ را تشکیل دهید.

پاسخ

ابتدا از زیرمجموعه هایی با کمترین عضو شروع می کنیم. سپس آنها را تحت یک مجموعه می نویسیم:

$\large P(A)=\left \{ \varnothing,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\} \right \}$

4-22 زیرمجموعه سره (محض)

زیرمجموعه سره به زیرمجموعه هایی از مجموعه گفته می شود که برابر با خود مجموعه مادر نباشند. پس اگر این شرط برقرار باشد، مجموعه B زیرمجموعه سره مجموعه A است، این گزاره را به صورت زیر نمایش می دهیم:

(7)

$\large B\neq A , B\subseteq A $

زیرمجموعه سره را به صورت زیر هم نمایش می دهند(در نماد $\subseteq$ خط زیر به معنای تساوی است):

(8)

$\large B\subset A $

از تمامی زیرمجموعه ها، تنها یک زیرمجموعه سره نیست. پس تعداد زیرمجموعه های سره به راحتی برای مجموعه A با n عضو قابل محاسبه است:

(9)

تعداد زیرمجموعه های سره $\large =2^{n}-1$

5-22 جمع بندی فصل

در این فصل با زیرمجموعه، برخی خواص و نتایج آن و همچنین تعداد زیرمجموعه ها، مجموعه توانی و زیرمجموعه های سره (محض) آشنا شدیم.

*1- تعداد زیرمجموعه های B={1,7,6,-2,1} را محاسبه کنید و سه زیرمجموعه را به دلخواه ذکر کنید.

*2- تعداد زیرمجموعه های سره مجموعه P(A) در مثال 22-2 را محاسبه کنید.( یعنی تعداد اعضای P(P(A)) ) و دو زیرمجموعه را به دلخواه بنویسید.

*3- جواد خیابانی 11 پیشکسوت ورزشی را برای ضبط مستند تاریخ ورزش ایران دعوت می کند. آنها مختارند که این دعوت را بپذیرند یا رد کنند. قرار است این پیشکسوت ها دور یک میز درباره تاریخ ورزش ایران صحبت کنند و جواد خیابانی در پشت صحنه حضور دارد و سوال می پرسد. چند حالت مختلف برای تشکیل این میزگرد وجود دارد؟ (کجا نشستن پیشکسوتان دارای اهمیت نیست؛ صرفا حضور یا عدم حضور آن ها را در نظر بگیرید)

*4- طهماسب یک تیم گل کوچک تشکیل داده است. تیم طهماسب چهار عضو دارد ولی در ترکیب اصلی تنها سه یا دو بازیکن قرار می گیرد. او به چند حالت می تواند ترکیب اصلی را انتخاب و اعلام کند؟(پست بازیکنان در اعلام ترکیب فاقد اهمیت است)